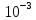1. Индивидуальное задание

Получить таблицузначенийфункцииf(y) для рядаравноотстоящих(с шагомh) значенийyє [c,d].

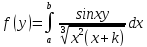
Численный метод интегрирования должен обеспечивать точность .

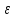Значение параметра k–абсциссаточки минимума функции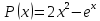на отрезке [m; n].

Провести интерполяцию полученных значений функции f(y), обеспечив погрешность интерполяции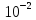

Исходные данные:

a	b	c	d	h	m	n
0.1	0.2	0.3	0.5	0.02	0	1

2. Постановка задачи

В данной курсовой работе требуется получить таблицу значенийфункцииf(y)для рядаравноотстоящихзначенийy є [c, d] с заданным шагомh. Функцияf(y) - этоопределенный интеграл с известными пределами интегрированияаиb, который необходимо вычислитьчисленнымметодомс заданной точностью .

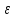Прежде чем приступать к последовательному нахождению значений определенного интеграладля каждого из значенийy, необходимо вычислить содержащийся в интегралепараметр k, который является абсциссой точкиминимумафункции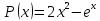на заданном отрезке[m; n]. Для этого нам потребуетсяисследоватьзаданную функцию с точки зрения ееунимодальностина заданном отрезке.

После нахождения минимума функции, подставимпараметр kв знаменатель подынтегральной функции, получивготовуюформулу для расчета.

Далее находим значения функции f(y)для каждого значенияy, вычисляя каждый разопределенныйинтеграл.

Полученные значения функции f(y) требуетсяпроинтерполировать, обеспечив заданнуюпогрешностьинтерполяции10^-2. Подтверждением правильности интерполяционного полинома является равенство его значений в узлах полинома и в одной из промежуточных точек.

Последовательность решения задачи показана ниже в виде схемыалгоритма.

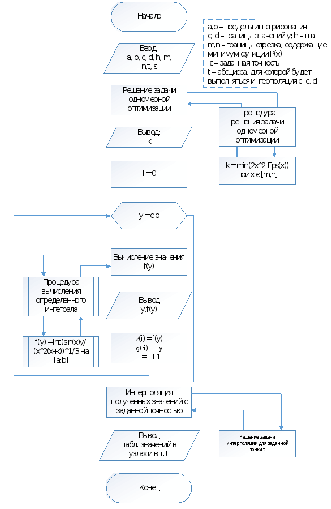
3. Выбор и обоснование используемых методов

Решение данной задачи требует использование трехчисленных методов:

1. Численный метод одномернойоптимизации

2. Численный метод вычисления определенногоинтеграла

3. Метод интерполированияфункции

Для решения задачи одномерной оптимизациибудет использован методзолотого сечения. Этот метод эффективен с точки зренияколичества вычислений функций на отдельной итерации, хотя ипроигрываетметодудихотомиипоколичествутребуемых итераций для достижения заданной точности.

Для вычисления определённогоинтегралабудем использовать формулуСимпсона, так как в состав нашей подынтегральной функции входяттригонометрическиефункции, а, следовательно, подынтегральная функциинелинейная. Для обеспечения требуемой точности интегрирования будем использоватьметод двойного просчета, в котором достижения заданной точности проверяютсяправилом Рунге.

Для интерполированияполученных значений функцииf(y)будет использована формулаЛагранжа с автоматической перенумерацией узлов. Хоть у нас и равноотстоящие узлы, для которых интерполяционные формулы Ньютона удобней при расчете, формула Лагранжа даст больший порядок точности, потому что при ее использовании возможно задействовать большее количество узлов, чем в формулах Ньютона, которыми можно интерполировать либотолько влево, либотолько вправо.

1. Метод золотого сечения

В основу метода положено разбиение отрезка неопределенности [a;b] всоотношениизолотогосечения, такого, чтоотношениедлиныегобольшейчасти ковсейдлинеотрезка равно отношениюдлиныегоменьшейчасти кдлинебольшейчасти.

В методе золотого сечения каждаяточка (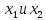) осуществляет золотое сечение отрезка.

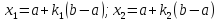
Точка 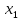осуществляет золотое сечениене толькоотрезка[a; b], но и отрезка[a; 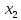].Аналогично с точкой. Это приводит к тому, что значение целевой функции на каждой итерации (кроме первой) вычисляетсяодинраз.

Сокращение отрезка неопределенности идет следующим образом:

1. Если

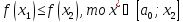
2. Если

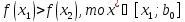
После каждой итерации длина отрезка неопределенности сокращается в 1.618 раза. Длина конечного отрезка неопределенности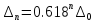, где.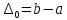

Условиеокончанияпроцесса итераций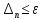. Отсюда находим количество итераций, необходимых для достижения точки минимума:

Методом золотого сечения можно найти минимум функции толькопри условии, что отрезок содержит единственный минимум, то есть, целевая функция на данном отрезке – унимодальная.

1. Проверка унимодальности

Методом золотого сечения можно найти минимум только при условии, если отрезок содержит единственный минимум, то есть целевая функция на данном отрезке –унимодальна.

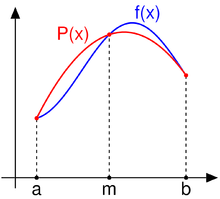
Проверимусловиеунимодальности для заданного в курсовой работе отрезка[m, n].

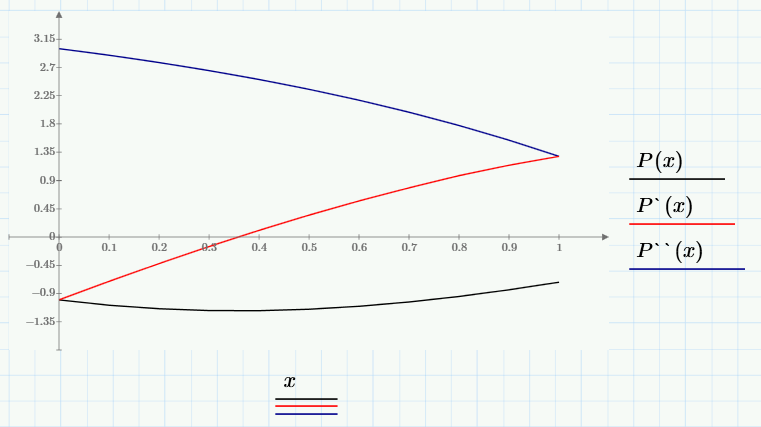
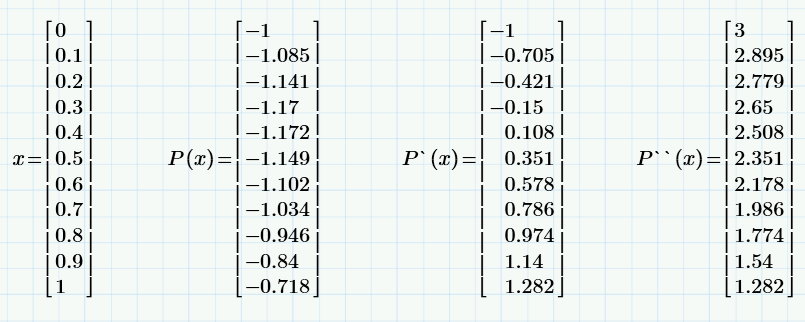
Как видно из графика и значений функции, ее первой и второй производных, функция P(x)на отрезке[0, 1]унимодальна, так как выполняются необходимые условия:

1. Для дифференцируемойфункции f(x), еепроизводнаяf′(х) -неубывающая.

2. Для дважды дифференцируемойфункции f(x) выполняется неравенствоf``(х) ≥ 0

2. Метод Симпсона

Суть метода заключается в приближенииподынтегральнойфункциина отрезке [a,b] интерполяционным многочленомвторойстепениP₂(x), то есть приближение графика функции на отрезкепараболой. Метод Симпсона имеетпорядокпогрешности4и алгебраическийпорядокточности3.

Формулой Симпсона называется интегралот интерполяционного многочленавторойстепени на отрезке:

где ,и— значения функции в соответствующих точках (на концах отрезка и в его середине).

Общаяпогрешностьпри интегрировании по отрезкус шагом(при этом, в частности,,) определяется по формуле:

.

Однаконапрактикеиспользование этой формулыограниченов связи струдоемкостьюее вычисления, поэтому для реализацииметода Симпсона наПКмы будем использовать прием, имеющий названиеправило Рунге(илиметод двойного просчета). Этот прием основан надвукратномвычислении значения интеграла вначале с шагомh(где), а затем с шагом. Полученные значенияи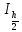могут быть применены дляоценкипогрешности интегрирования по формуле:

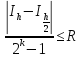
где k = 4 – для формулыСимпсона.

3. Интерполяционная формула Лагранжа

Пусть функция f(x)задана в(n+1)узлах, произвольно или равномерно расположенных на отрезке [a;b]: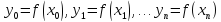

Требуется найти интерполирующий алгебраический многочлен 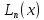, степени не вышеn, удовлетворяющий условию интерполяции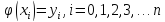, такой, что:

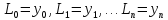
Будем искать вида:

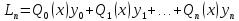
где 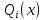– коэффициенты, зависящие только от узлов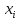,i= 0, 1, …nи текущего значенияx.

Для выполненияусловийинтерполяциинужно, чтобы

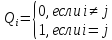
Этому требованию отвечает коэффициент вида:

Для интерполяционного многочлена Лагранжа выражение будет иметь вид:

\

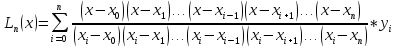Несмотря на громоздкость, одним из преимуществформулы Лагранжа является возможность ее записинепосредственнопозаданнойтаблицезначенийфункции. Для этого следует учесть следующее правило: формула содержит столькослагаемых, сколькоузловв таблице; каждое слагаемое – это произведение дробного коэффициента на соответствующее значение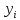; числитель коэффициента при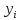содержит произведение разностей х со всеми узлами кроме, а знаменатель полностью повторяет числитель при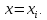

Оценкапогрешностиформулы Лагранжа:

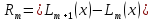
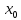Для того, чтобы уменьшитьпогрешностьинтерполяции, используется приемперенумерацииузлов исходной таблицы, последовательно выбирая в качествеи т.д. узлы,наиболееблизкорасположенныек искомой точке х, по возможности симметрично относительно точки. Такой прием позволяетуменьшитьстепеньинтерполяционного полинома для достижения требуемой точности ине использоватьвсе заданные узлы.

В данной курсовой работе перенумерацияузлов будет осуществляться с помощью сортировки «методом пузырьков».