3.2.3. Многорайонная и многоотраслевая модель

Ниже приводится пример модели, в которой учитываются не­которые из наиболее важных взаимосвязей между районами и от­раслями. Данная модель взята из наработок экономической комис­сии ООН, работавшей под руководством Я.Тинбергена¹.

Для характеристики переменных модели используются три типа индексов. Время обозначается обычным нижним индексом, например, отрасль обозначается верхним правым индексом,например, а район — верхним левым индексом (). Когда име­ется в виду отрасль (или район) вообще, символыили(или,или) используются без какого-либо указания номера. Общеечисло отраслей равно, число районов — равноR. Первой отрас­лью () является транспорт, особое положение которого в мо­дели объясняется ниже.

¹ См.: Методы разработки программ экономического развития. М.: Изд-во иностранной литературы. 1963. С. 171 — 176.

Переменными модели являются:

— объем производства продуктав районев течение-гопериода;

— цена продукта, производимого в районе;

— средняя цена продуктав районе;

— доход района;

— сбережения района;

— экспорт минус импорт продуктаиз района;

— количество продукта, производимого в районеи ис­пользуемого в районекак для потребления, так и для произ­водства;

— количество продукта, используемого в отрасли(длятекущего производства продукции) в районе;

— количество продукта, используемого для инвестицийв отрасльв районе.

Коэффициенты обозначаются следующими символами:

— норма сбережений, полученная на основе макроэкономи­ческой модели для длительного периода времени; предполагает­ся, что она едина для всей страны;

— запаздывание инвестиций, предполагаемое единым, хотяоно может быть легко дифференцировано для разных отраслей;

— транспортный фактор, показывающий повышение цены(в виде отношения) в результате перевозки продуктаиз района

в район;

— коэффициент затрат продуктапри производстве про­дуктав районе;

— коэффициент затрат продуктадля увеличения произ­водственной мощности отраслив районе;

— предельная склонность к потреблению продуктав рай­оне;

— отрезок кривой Энгеля для продукциив районе[см.уравнение (2)];

— коэффициенты, показывающие конкуренцию цен рай­онов в функциях спроса [см. уравнение (9)];

— коэффициенты, входящие в функцию спроса ми­рового рынка на продукт, поставляемый районом.

Уравнения, выражающие связи между этими переменными, можно подразделить на 10 групп. Каждая группа представляет определенную категорию уравнений. Количество уравнений в каждой группе показано с правой стороны.

Балансовое уравнение

Балансовые уравнения, для

при:

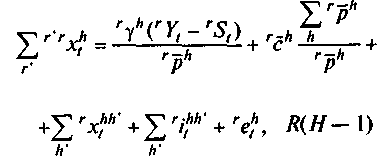
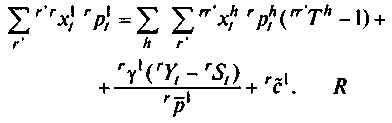
Уравнение затрат текущего производства

Уравнение инвестиционных затрат

Уравнение финансирования инвестиций

Уравнение, определяющее доход

Уравнение сбережений

Уравнение общего спроса

Уравнения распределения спроса:

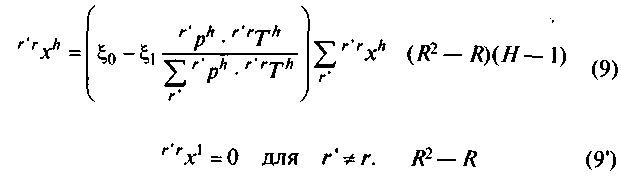
Уравнение, определяющее средние цены

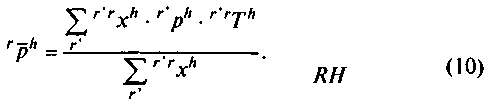
Группы уравнений (1), (3), (4) и (7) не требуют объяснения. В уравнениях группы (2) первые два члена на правой стороне пред­ставляют потребительский спрос, предположительно состоящий из постояннойи элемента, пропорционального общему объемупотребления. Для этой части спроса должны быть удовлетворены некоторые условия, обеспечивающие положительные значения переменных при всех реальных ситуациях. Кроме того, необходи­мо предположить, что

Это означает, что сумма потребительских расходов на каждый продуктравна общему объему потребления. Второе условие ка­сается цен, так что оно не может быть удовлетворено заранее. Однако поскольку в нашем способе использования модели на том этапе, когда другие переменные должны быть определены, цены являются данными, то это предположение сделать нетрудно.

Уравнение (5) устанавливает, что сумма всех инвестиционных затрат равна общему объему сбережений. При наличии импорта капитала его можно добавить к левой части уравнения.

Уравнение (6) выводится из определения чистого дохода в каж­дой отрасли:

Уравнение (8) устанавливает, что ценапродуктав любомрайоне, как правило, зависит от объемов производства этогопродукта в различных районах, причем производство в самом рай­онеоказывает набольшее влияние, чем производство в дру­гих районах. Уравнение (8) отражает влияние цены на общий спрос на продукт, производимый в районе. Этот спрос отри­цательно связан с ценой на продукты и объемами его производ­ства в других районах. Коэффициентотражает влияние всехдругих факторов и, следовательно, зависит, кроме всего прочего, от доходов тех стран, которые обеспечивают спрос. Это по суще­ству модель открытой экономики, и она предполагает незначи­тельное влияние национального дохода на относительные цены.

Уравнение (9) показывает, по какому «ключу» распределяется

общий спрос на продуктв районемежду различными '

районами-поставщиками. Решающей переменной этого распреде­ления является дробь, стоящая в скобках. Эта дробь является от­ношением цены, которая устанавливается райономза поставкупродуктав район, к средней цене поставки этого продукта извсех районов (для удобства расчетов эта цена умножена на). Чемменьше это «отношение» или относительная цена, тем больше объем поставок данного районав район. Коэффициентыи выражают эластичность этой взаимосвязи; чем больше, тем больше «реакция» на разницу цены продукта данного района исредней цены. Коэффициентыидолжны удовлетворять ус­ловию:

9

так чтобы итог, полученный по всем районам, составлялобщую величину спроса.

Что касается транспорта, то в отношении затрат (текущих и инвестиционных) он ничем не отличается от других отраслей [см. уравнения (3) и (4)]. Как следствие этого, транспорт входит в урав­нения (5) и (6) обычным образом, увеличивая доход страны и потребность в инвестициях. Однако не предполагается, что спрос остальных отраслей на услуги транспорта находится в каком-то отношении к их производству и инвестициям, т.е.Вместо этого предполагается, что спрос на услуги транспорта за­висит от количества продукта, перевозимого из районаврайон, и транспортных издержек на перевозку продукта

, которые в свою очередь зависят от расстояния меж­дуи, цены продукта и других расходов, связанных с перевоз­кой данного вида продукта. «Законы», определяющие количества перевозимых продуктов, уже выражены уравнениями (9).

Далее предполагается, что сами услуги транспорта не могут «перевозиться» из района в район, т.е. дляИз этого следует, что в отношении транспортных услуг нет раз­ницы междуи

Данную модель можно использовать в процессе «планирования по стадиям». Один из вариантов расчета может быть осуществлен в следующей последовательности. Предположим, что существую­щая производственная мощность всегда используется полностью. Это означает, что в любом периоде t все объемы производстваопределяются инвестициями предыдущего периода. Далее, предполагается, что норма сбережений s уже выбрана на основе более простой модели, а это означает, что общий объем инвести­ций известен. Поскольку цены также известны согласно уравне­нию (8), то отдельные элементы инвестицийопределяются врезультате решения следующей задачи на оптимум: максимизиро­вать национальный доходпри условии, что общий объем инвестиций годазадан. Фактическизависит от трехгрупп переменных года [см. уравнение (6)]. Из них можно выразить с помощью (8) черезС помощью (1) и (9)можно выразить через цены, кото­рые уже выражены через, и через сами. Следовательно,есть функция всех элементов. С другой стороны, сбереже­ния периодазависят от, которые можно выразить с помо­щью (4) через, а все другие переменные, входящие в, ужеизвестны. Таким образом, и ограничивающие условия касаются только

Определив эти последние переменные так, чтобы мак­симизировать национальный доход, мы можем затем исполь­зовать модель для дальнейшего уточнения производственного плана в году. Неизвестные этого второго расчета приводятсяниже; в скобках указано их количество:

Таким образом, количество неизвестных равно

, а уравнений —. Сле-

довательно, неизвестные будут удовлетворять одному условию, а именно равновесию платежного баланса:

Эту модель можно обобщить и конкретизировать различными способами. Поскольку она является только примером, мы не вда­емся в дальнейшие подробности.