2.2 Постановка математической задачи оптимизации

Задачей оптимизации в математике, информатике и исследованиях операций называется задача нахождения экстремума (минимума или максимума) некоторой функции. Обычно рассматривается целевая функция в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

В процессе проектирования ставится обычно задача определения наилучших или оптимальных, в некотором смысле, структуры или значения параметров объектов. Условие оптимальности считается критерием оптимальности. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической. Задача выбора оптимальной структуры является структурной оптимизацией.

Стандартная математическая задача оптимизации формулируется следующим образом. Среди элементов x₁,x₂, . . . , x_n, образующих множества Χ, найти такой элемент x⁰ , который доставляет экстремальное (минимальное или максимальное) значение f(x⁰) заданной функции f(x).

Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

1. Допустимое множество— множество ;

2. Целевую функцию— отображение ;

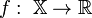3. Критерий поиска(max или min).

Тогда решить задачу оптимизации означает одно из:

1. Показать, что .

2. Показать, что целевая функция 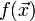не ограничена снизу.

3. Найти .

4. Если 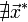, то найти .\

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x₀ таких, что всюду в некоторой их окрестности для минимума и для максимума.

Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.[6]

2.3 Модель транспортной задачи

Рассмотрим транспортную задачу, в которой речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям.

Пусть имеется m пунктов производства однородного продукта (добыча руды в карьерах, производство автобусов, кондитерских изделий, компьютеров и т.д.) и n пунктов потребления этого продукта. Мощности пунктов производства составляют а_i единиц однородного продукта, а потребности каждого j-го пункта потребления равны единиц. Известны затратына перевозку единицы продукта отi-го поставщика j-му потребителю. Составить такой план перевозок, при котором суммарные затраты на все перевозки были бы наименьшими.

Пусть спрос и предложение совпадают, т.е. Такую транспортную задачу называютсбалансированной (закрытой). При этом предполагается, что вся продукция от поставщиков будет вывезена и спрос каждого из потребителей будет удовлетворен.

Составим математическую модель задачи. Обозначим через количество продукта, перевозимого изi-го пункта производства вj-й пункт потребления. Тогда матрица:

план перевозок.

Матрицу называютматрицей затрат(тарифов).

Внесем исходные данные и перевозки в транспортную таблицу:

Таблица 2.1 – Матрица затрат

bj ai	b1	b2	...	bn
a1	c11 x11	c12 x12	...	c1n x1n
a2	c21 x21	c22 x22	...	c2n x2n
...	...	...	...	...
am	cm1 xm1	cm2 xm2	...	cmn xmn

Предположим, что транспортные затраты прямо пропорциональны количеству перевозимого продукта. Тогда стоимости перевозок определяются формулой:

,

а суммарные затраты выражаются функцией цели:

которую необходимо минимизировать при ограничениях:

(весь продукт из каждого i-го поставщика должен быть вывезен полностью),

(спрос каждого j – го потребителя должен быть полностью удовлетворен).

Из условия задачи следует, что все

Итак, математическая модель сбалансированнойтранспортной задачи имеет вид:

при ограничениях: