ЭЛЕКТРОМАГНЕТИЗМ Лабораторный практикум по физике Часть 2

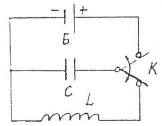
ЛАБОРАТОРНАЯ РАБОТА №20

ИССЛЕДОВАНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Цель работы – изучить параметры и характеристики колебательного контура.

Краткие сведения из теории

Если зарядить конденсатор от батареи до напряжения Ua

(рис. 20.1), а затем повернуть переключатель К, то конденсатор начнет разряжаться через катушку и в контуре возникнут электромагнитные колебания.

Рассмотрим, как происходят эти колебания в контуре, сопротивление которого R = 0. При замыкании контура в нем появляется ток I, создающий магнитное поле. Изменение магнитного поля тока приводит к возникновению в цепи электродвижущей силы самоиндукции Ei, замедляющей быстроту разряда. При уменьшении тока возникает электродвижущая сила, направленная в ту же сторону, что и вызвавший ее появление ток. Это приводит к тому, что

после разряда конденсатора ток не прекращается сразу, а в течение некоторого времени продолжает течь в том же направлении и перезаряжает обкладки конденсатора. Затем процесс разряда начинается снова, но протекает теперь в обратном направлении. В результате вторичного перезаряжения конденсатора система возвращается в исходное состояние, после чего повторяются те же процессы. Время от начала процесса до конца вторичного перезаряжения называется периодом собственных колебаний.

В начальный момент, когда конденсатор полностью заряжен, в нем накоплена электрическая энергия: WE = CU02 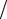2. Во время

разряжения конденсатора электрическая энергия превращается в энергию магнитного поля катушки и, когда конденсатор полностью разряжен, вся электрическая энергия переходит в магнитную:

WM = LI02 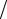2, где I0 – наибольшая величина тока, в контуре.

60

При перезаряжении конденсатора энергия магнитного поля снова превращается в энергию электрического поля. В контуре возникают незатухающие электромагнитные колебания.

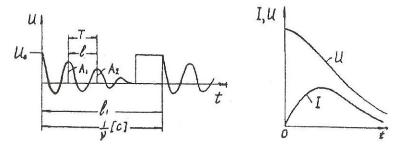
Проводники контура всегда обладают электрическим сопротивлением, поэтому часть энергии в процессе колебаний расходуется на нагрев проводников. Вследствие этого амплитуда электромагнитных колебаний в контуре постепенно уменьшается и в нем происходят затухающие колебания (рис. 20.2). При достаточно большом сопротивлении контура или малой индуктивности колебания в нем вообще не возникают, а происходит так называемый апериодический разряд конденсатора (рис. 20.3).

61

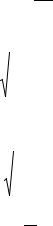
Подставим последние выражения в (20.1):

Как известно, дифференциальное уравнение (20.4) описывает затухающие колебания. Его решение:

Если (20.1) записать в виде Cq + IR = −L dIdt и продифференци-

ровать по времени, то получим уравнение того же типа, что и

(20.4):

из чего следует, что ток в контуре также совершает затухающие колебания, для которых значения β, ω и Т определяются по фор-

мулам (20.6), (20.7) и (20.7а).

Из (20.7) и (20.7а) следует, что в контуре возможны затухаю-

62

(частота и период – действительные величины) или R < 2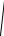CL . Ес-

ли R > 2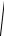CL , то частота и период мнимые, колебаний нет и проис-

ходит апериодический разряд конденсатора (см. рис. 20.З). Сопротивление, при котором частота ω обращается в нуль,

называется критическим:

кр C

В этом случае конденсатор также разряжается апериодически. Для характеристики степени затухания колебаний, кроме ко-

эффициента затухания β, используется еще логарифмический декремент затухания.

Логарифмическим декрементом затухания колебаний называется натуральный логарифм отношения двух значений напряжения, разделенных интервалом времени, равным периоду колебаний:

63

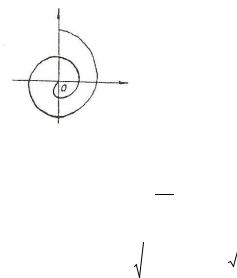
В ряде случаев удобно изучать колебательный процесс в системе координат I и U, т.е. откладывать

Uпо оси абсцисс величину силы тока в контуре в заданный момент времени, а по оси ординат – напряжение на конденсаторе в тот же момент времени.

Плоскость U − I носит название плос-

Iкости состояний или фазовой плоскости, а кривая, изображающая зависи-

мость напряжения от силы тока, назы- Рис. 20.4 вается фазовой кривой (рис. 20.4).

Найдем фазовую кривую для контура, сопротивление которого R = 0. В этом случае β = 2RL = 0 и из (20.5), (20.7) и (20.7а) следует:

Уравнения (20.12) описывают незатухающие колебания. Исключив из них время t , получим уравнение фазовой кривой:

Это уравнение эллипса. Эллипс получается в результате сложения двух взаимно перпендикулярных гармонических колебаний (20.12), сдвинутых по фазе на четверть периода. В контуре, сопротивление которого R > 0, происходят затухающие колебания напряжения (20.5) и тока:

64

В этом случае амплитуды напряжения и тока в контуре непрерывно убывают, не повторяясь через период времени, и фазовая кривая получается незамкнутой (см. рис. 20.4).

Приборы и оборудование

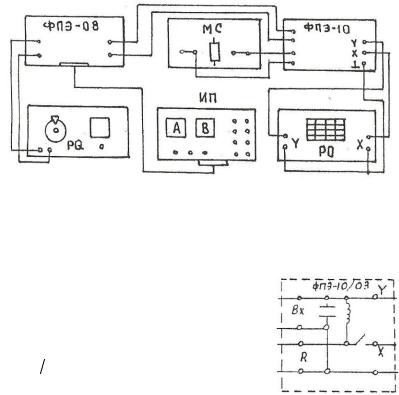
PQ – генератор звуковых сигналов, РО – осциллограф; ФПЭ-10 – модуль с колебательным контуром; ФПЭ-08 – преобразователь импульсов; ИП – источник питания; МС – магазин сопротивлений.

Принципиальная схема экспериментальной установки изображена на рис. 20.5.

Рис. 20.5

В работе для получения колебаний в контуре используется модуль ФПЭ-10 с контуром, изображенным на рис. 20.6.

Происходящие в контуре затухающие колебания (см. рис. 20.2) наблюдаются на экране осциллографа. Цикл заряжения и разряжения конденсатора

65

хающих колебаний, которому на рис. 20.2 соответствует отрезок l . Из пропорции Tl = l1ν получаем

Порядок выполнения работы

Задание 1. Измерение периода, логарифмического декремента

ипараметров L, С, R колебательного контура

1.Ознакомиться с работой звукового генератора и электронного осциллографа в режиме измерения амплитуды синусоидального напряжения и получения фигур Лиссажу.

2.Подготовить приборы к работе.

2.1.Установить следующие параметры выходного напряжения звукового генератора: частота 250 Гц, напряжение 2–3 В.

2.2.На преобразователе импульсов ФПЭ-08 нажать клавишу «П» и правую клавишу «Cкважность грубо».

2.3.Ручку магазина сопротивлений поставить в положение «1» и нажать клавишу «х102».

3. Включить лабораторный стенд и приборы.

4. Получить на экране осциллографа устойчивую картину колебаний (см. рис. 20.2).

5. Измерить расстояния l, l1 и вычислить период колебаний по формуле (20.14).

6. Измерить амплитуду колебаний U10 , U20 , U30 и, комбини-

руя их попарно, вычислить по (20.9) логарифмический декремент затухания λ . По формуле (20.10) определить коэффициент затухания β. Результаты измерений и расчетов занести в табл. 20.1.

7. Выполнить измерения пп. 5, 6, включив в магазине сопро-

тивления 100, 300, 500, 600 Ом.

Т а б л и ц а 20.1

66

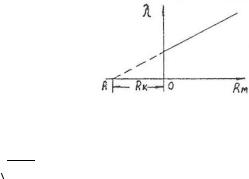
8. Построить график зависимости логарифмического декремента затухания λ от сопротивления Rм магазина (см. рис. 20.7), откладывая значения Rм по оси абсцисс от произвольной точки 0 в экстраполируя график к λ = 0. Полное сопротивление контура R

сопротивлений Rмк, при котором наблю-

дается апериодический разряд конденсатора. Согласно (20.8) должно быть Rк + Rмк = 2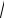LC . Проверить расчетом это соотношение.

Задание 2. Исследование фазовых кривых

Для наблюдения на экране фазовой кривой на вертикально отклоняющие пластины осциллографа подают напряжение с обкладок конденсатора, а на горизонтально отклоняющие пластины –

напряжение U R с клемм магазина сопротивлений Rм , пропорциональное току U R = IRм . Таким образом, на экране осциллографа

изображается зависимость напряжения U на обкладках конденсатора от тока I в контуре.

1.Включить осциллограф. Получить на экране фазовую кри-

вую (см. рис. 20.4).

2.Установить картину в центре экрана.

3.Вращая ручку магазина сопротивлений, получить фазовые кривые при различных сопротивлениях.

67

4. Измерить значения напряжения, разделенные периодом колебаний, т.е. расстояния от центра фазовой кривой до точки пересечения витков спирали с осью напряжения U , и вычислить логарифмический декремент затухания:

λ = 2,3lg U10 .

U20

Аналогичным образом вычислить логарифмический декремент по значениям силы тока I, измеренным через период колебаний:

λ = 2,3lg I10 .

I20

Измерения выполнить по всем виткам фазовой кривой. Результат записать в табл. 20.2.

Т а б л и ц а 20.2

5.Повторить измерения п. 4 при значениях сопротивления магазина 100, 200, 300, 400, 500, 600 0м.

6.Зарисовать фазовую кривую при апериодическом разряде конденсатора.

7.Рассчитать погрешность определения λ :

∆λ = [(lnU10 )′]2 ∆U102 +[(lnU20 )′]2 ∆U202 ,

где ∆U – погрешность измерения U на экране.

Контрольные вопросы

1.Что такое колебательный контур, и как в нем возникают колебания?

2.Что такое логарифмический декремент затухания?

3.Что представляет собой апериодический разряд в контуре,

ипри каких условиях он происходит?

68

4.Что такое фазовая плоскость и фазовая кривая?

5.Какова форма фазовой кривой: а) при незатухающих колебаниях; б) при затухающих колебаниях; в) при апериодическом разряде?

Библиогр.: [1, 2, 11].

ЛАБОРАТОРНАЯ РАБОТА №21

ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Цель работы – изучить зависимость силы тока в колебательном контуре от частоты источника ЭДС, включенного в контур, и измерить резонансную частоту контура.

Краткие сведения из теории

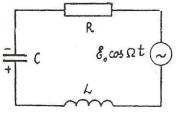
Рассмотрим процессы, протекающие в колебательном контуре, подключенном к источнику, ЭДС которого изменяется по гармоническому закону:

где U – напряжение на конденсаторе емкостьюС; I – ток в контуре. Полагаем, что мгновенные

Падение напряжения на катушке индуктивностью L

69