Линейные операторы в Евклидовом пространстве. Ортогональный оператор.

Определение. Линейный оператор f пространства называется ортогональным, если.

Если f – ортогональный вектор, то ,. Еслиf и g – ортогональные операторы, то fg – ортогональный оператор.

Определение. Квадратная матрица А называется ортогональной, если .

Теорема 5.14. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.

Теорема 5.15. Линейный оператор тогда и только тогда является ортогональным, когда он задаётся ортогональной матрицей.

Самосопряжённый (симметрический) оператор.

Определение. Линейный оператор f пространства называется самосопряжённым (симметрическим), если

.

Теорема 5.17. Линейный оператор задаётся в ортонормированном базисе симметрической матрицей тогда и только тогда, когдаf – самосопряжённый оператор.

Теорема 5.18. Линейный оператор тогда и только тогда является самосопряжённым, когда найдётся ортонормированный базис, состоящий из собственных векторов линейного оператораf.

Теорема 5.19. Для любой симметрической матрицы А существует такая ортогональная С, что САС− диагональная.

Квадратичные формы. Приведение квадратичной формы к каноническому виду.

Определение. Квадратичной формой F от n переменных называется многочлен от этих переменных с действительными коэффициентами, каждое слагаемое, которого имеет вторую степень.

Таким образом

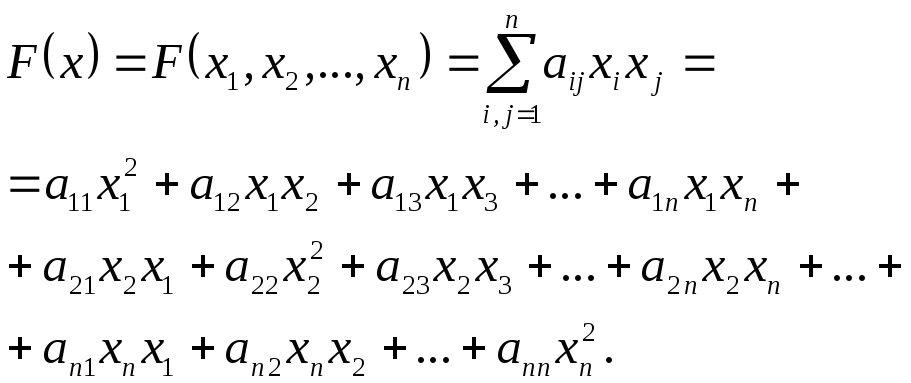(1)

Так как , тоF записывают таким образом, что . При этом матрицаявляется симметрической и называется матрицей квадратичной формыF.

Обозначим

X = , тогдаx^T = (x₁,x₂,…,x_n).

Квадратичная форма принимает вид:

F(X) = X^TAX.

Подвергнем переменные x₁,…,x_n линейному преобразованию вида:

x_i = b_ijy_k , где y₁,…,y_n − новые переменные.

Тогда матрица B = (b_ij) – матрица, выражающая старые переменные через новые. Легко проверить, что в этом случае

X = BY, где

Y = (2)

Лемма 6.1. Пусть произведение матриц A и B определено, тогда (АВ)^Т = В^ТА^Т.

Лемма 6.2. Квадратичная форма от n неизвестных с матрицей А, после выполнения линейных преобразований неизвестных с матрицей В превращается в квадратичную форму от новых неизвестных с матрицей этой квадратичной формы вида

В^ТАВ

Линейное преобразование называется невырожденным, если матрица В этого преобразования, то есть |B| 0.

Очевидно, что если |B| 0 иХ = ВУ, то У = В^-1У – преобразование ответное к линейному преобразованию вида (2).

Определение. Квадратичная форма называется канонической, если еë матрица является диагональной.

Теорема 6.1. (Алгоритм Лагранжа)

Любая квадратичная форма с помощью невырожденного линейного преобразования переменных приводится к каноническому виду.

Нормальный вид квадратичной формы

Определение. Канонический вид квадратичной формы, каждый ненулевой коэффициент которого равен ±1, называется нормальным.

Лемма 6.3. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных приводится к нормальному виду.

Теорема 6.2. (Закон инерции квадратичных форм)

Число положительных и число отрицательных коэффициентов в нормальном виде

квадратичной формы не зависит от выбора невырожденного линейного преобразования переменных, приводящих эту форму к нормальному виду.

Определение. Число положительных (отрицательных) коэффициентов в нормальном виде квадратичной формы называется положительным (отрицательным) индексом инерции этой формы.