Многочлены с рациональными коэффициентами.

Так как корни многочленов исовпадают для любого, то можно считать, что коэффициентыявляются целыми числами (такой многочлен называетсяцелочисленным).

Лемма 2.7. Если целое число – корень целочисленного многочлена, тоявляется делителем свободного члена.

Следующие результаты решают вопрос о рациональных корнях целочисленного многочлена.

Лемма 2.8. Если целочисленный многочлен, старший коэффициент которого равен 1, имеет рациональный корень, то этот корень является целым числом.

Теорема 2.8. Множество всех рациональных корней целочисленного многочлена =+…++

совпадает с множеством всех целых корней многочлена , деленных на.

Матрицы и определители.

Таблица вида , либо,,, где– элементы некоторого фиксированного множества называетсяпрямоугольной матрицей размерности . Если , то матрица называетсяквадратной порядка. Матрицы, размерности иназывается соответственноматрицей-строкой и матрицей-столбцом. Элементы называютсядиагональными. Квадратная матрица, у которой все недиагональные элементы равны нулю, называется диагональной. Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной и обозначается .

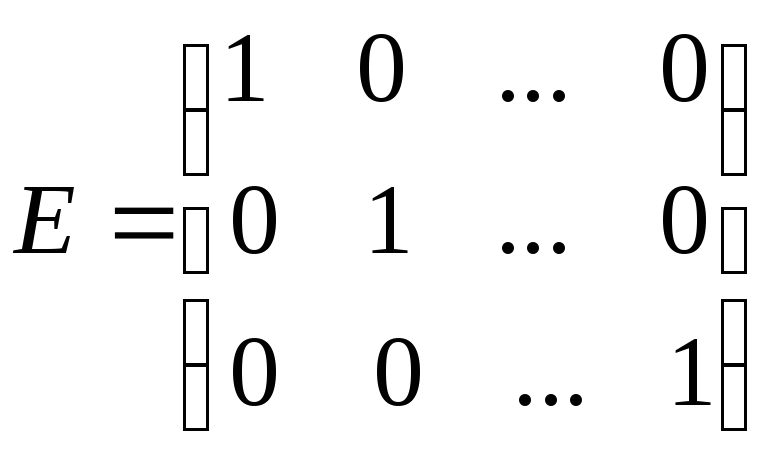Определение 3.1. Минором некоторого элемента квадратной матрицыА порядка , называется тот определитель-го порядка, который получается из данного путем вычеркивания той строки и того столбца, на пересечении которых стоит данный элемент и обозначается.

Определение 3.2. Определителем квадратной матрицы -го порядка называется выражение

.

Используются также следующие обозначения:

.

Матрица, полученная из данной матрицы путем замены строк соответствующими столбцами, называетсятранспонированной и обозначается .

Свойства определителей.

1. При транспонировании матрицы ее определитель не меняется.

2. При перестановке любых двух строк местами определитель меняет знак на противоположный.

3. Теорема 3.1. (о разложении определителей по элементам i-ой строки) .

4. Если определитель имеет две одинаковые строки, то он равен нулю.

5. Если все элементы какой-либо строки определителя умножить на одно и то же число, то определитель умножиться на это число.

6. Если все элементы какой-либо строки равны нулю, то определитель равен нулю.

7. Если все элементы какой-либо строки представляют собой сумму двух слагаемых, то определитель равен сумме соответствующих определителей.

8. (основное свойство) Определитель не измениться, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Свойство 1. Позволяет формировать все вышеперечисленные утверждения и для столбцов.

Определение 3.3. Алгебраическим дополнением элемента определителя называется минор, умноженный наи обозначается.

Следовательно, .

Теорема 3.2. (об алгебраическом дополнении).

Сумма произведений элементов строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна нулю.

Ранг матрицы.

Определение 3.4. Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы, обозначаетсяили.

Отличный от нуля минор k-го порядка, где k = , называетсябазисным минором. Строки и столбцы, матрицы , на которых построен базисный минор, называются соответственнобазисными строками и столбцами. Очевидно, что на строки и столбцы можно смотреть как на матрицы-строки и матрицы-столбцы. Поэтому, если – строки матрицы, и– какие-либо числа, то выражение вида

является матрицей-строкой и называется линейной комбинацией строк .

Если -- строка матрицы, то говорят, чтолинейно выражается через строки .

Строки называютсялинейно зависимыми, если существуют такие одновременно неравные нулю числа , что(*)

– нулевая строка. Если же (*) имеет место тогда и только тогда, когда все , то строки называютсялинейно независимыми.

Теорема 3.3. (о базисном миноре). Любая строка матрицы является линейной комбинацией ее базисных строк, которые линейно независимы.

Теорема 3.4. ( необходимое и достаточное условие равенства нулю определителя).

Для того, чтобы определитель был равен нулю, необходимо и достаточно , чтобы все строки (столбцы) были линейно зависимы.

Элементарными преобразованиями строк (столбцов) матрицы являются:

1. умножение элементов любой строки (столбца) на отличное от нуля число;

2. перестановка строк (столбцов) местами;

3. прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на некоторое число;

4. транспонирование.

Теорема 3.5. (об элементарных преобразованиях). В результате элементарных преобразований ранг матрицы не меняется.