Корни многочлена.

Число с называется корнем многочлена = +…+, если=.

Лемма 2.1. Остаток от деления f(x) на x-c равен f(c).

Таким образом, число с тогда и только тогда является корнем f(x), когда f(x) делится на x-c.

Пусть = (x–c)q(x) + r, и q(x) = .

Сравнивая коэффициенты при одинаковых степенях, получаем

, , , … , ,–схема (метод) Горнера.

Пусть=, причемне делится наx-c. Тогда число с называется k-кратным корнем f(x), а число k – кратностью корня с в многочлене f(x).

Производной многочлена f(x) называется многочлен (n-1)-ой степени

.

k-ая производная – это производная от (k–1)-ой производной. Очевидно, что

, и

Лемма 2.2. 1)

2)

3)

Лемма 2.3. Если число с – k-кратный корень , то приk > 1 с является (k – 1) – кратным корнем , если жеk = 1, то с не является корнем для .

Основная теорема алгебры.

Любой многочлен с любыми числовыми коэффициентами, степень которого не меньше 1, имеет хотя бы один корень, в общем случае комплексный.

Следствия из основной теоремы.

Лемма 2.4. Пусть ,, тогда

Теорема 2.5. Для любого многочлена степениn1 существует единственное разложение

, где – корень.

Следствие 2.5.1. Любой многочлен степени n1 имеет ровно n корней, если каждый из корней считать столько раз, какова его четность.

Следствие 2.5.2. Если истепениn имеют равные значения более чем при n различных значениях неизвестного, то

Следствие 2.5.3. Пусть , тогда существует хотя бы одно число с такое, что

Можно решить обратную задачу. А именно, построить многочлен степени n, принимающий наперед заданные значения при n + 1 различных значениях неизвестного. Например,

– интерполяционная формула Лагранжа, где и всеразличны.

Если и все– корни, то имеют место формулы Виета:

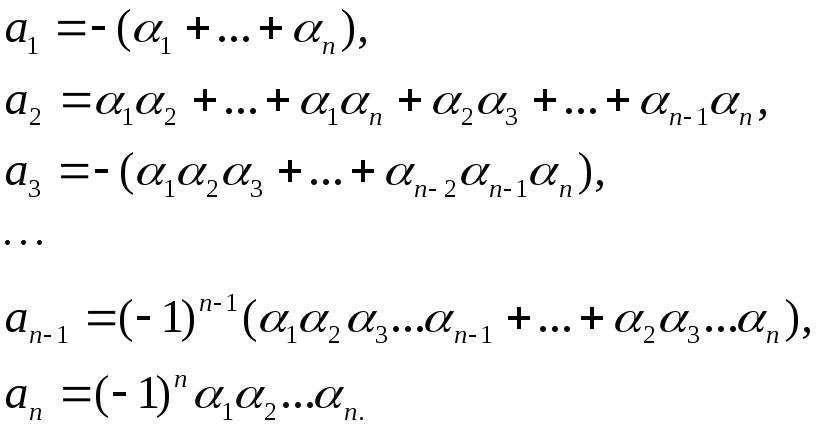
Многочлены с действительными коэффициентами.

Теорема 2.6. Если – комплексный корень, то и– корень.

Следствие 2.6.1. Если – комплексныйk-кратный , то и–k-кратный корень.

Вывод: Любой многочлен с действительными коэффициентами представим единственным образом (с точностью до порядка сомножителей) в виде произведения старшего коэффициента и многочленов с действительными коэффициентами:

линейных, вида , и квадратных, вида (*).

Многочлены вида и вида (*) называютсянеприводимыми (над множеством действительных чисел!).

Рациональные дроби.

Пусть и– многочлены с действительными коэффициентами.

Частное вида называетсярациональной дробью.

Рациональная дробь называется несократимой, если и– взаимно просты.

Лемма 2.5. Любая рациональная дробь равна некоторой несократимой дроби, определенной с точностью до множителя нулевой степени, общего для числителя и знаменателя.

Рациональная дробь называетсяправильной, если .

Нулевой многочлен, т.е. 0 , считается правильной дробью.

Лемма 2.6. Любая рациональная дробь представима единственным образом в виде суммы многочлена и правильной дроби.

Правильная рациональная дробь называетсяпростейшей, если ,k1, где – неприводимый многочлен и.

Теорема 2.7. Любая правильная рациональная дробь представима в виде суммы простейших, причем единственным образом.