Операции над матрицами.

Пусть ,.

Тогда их сумма – это матрица .

Операции сложения матриц обладают следующими свойствами:

1. А + В = В + А (коммутативности)

2. А + (В + С) = (А + В) + С (ассоциативности)

3. А + 0 = А , 0-нуль-матрица

4. А + (-А) = 0 , где (-А) = (-)- матрицапротивоположная к А

Произведением матрицы А = () на числоназывается матрицаА=(), каждый элемент которой равен произведению соответствующего элемента матрицыА на .

Справедливы следующие свойства:

1. 1А = А

2. (+)А = А +А

3. (А+В) = А +В

4. (А) = ()А

Пусть размерности матриц А и В – соответственно mn и np:

А =,В =

Тогда произведение А на В определяется как матрица С = АВ = () размерностиmp и =++…+

Справедливы следующие свойства:

1. А(ВС)=(АВ)С

2. (АВ)= (А)В=А(В)

3. А(В+С)=АВ+АС

4. АЕ=ЕА=А

Обратная матрица

Квадратная матрица называется обратной к квадратной матрице А, если

А=А=Е

Квадратная матрица А называется невырожденной, если 0

Теорема 3.6. Для любой невырожденной матрицы существует единственная обратная к ней.

Системы линейных уравнений

Система вида

(1)

называется системой m линейных уравнений с n неизвестными ,,...,.

Числа называются коэффициентами системы,,,…,- свободные члены.

Решением системы (1) называется упорядоченная последовательность чисел ,,…,, которая, будучи подставленной, в (1) вместо неизвестных, обращает все уравнения (1) в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет решений.

Система называется определённой, если имеет единственное решение, и неопределённой, если она имеет, по крайней мере, два решения.

Системы равносильны или эквивалентны, если множество их решений совпадают.

Системы n линейных уравнений с n неизвестными

Обозначим:

-определитель системы,

Теорема 4.1. (правило Крамера):

Система (2), определитель которой отличается от нуля, имеет единственное решение,находящееся по формулам (Крамера):

Критерий Кронекера-Капелли совместности системы.

В системе (1) обозначим

А = (),В = ,

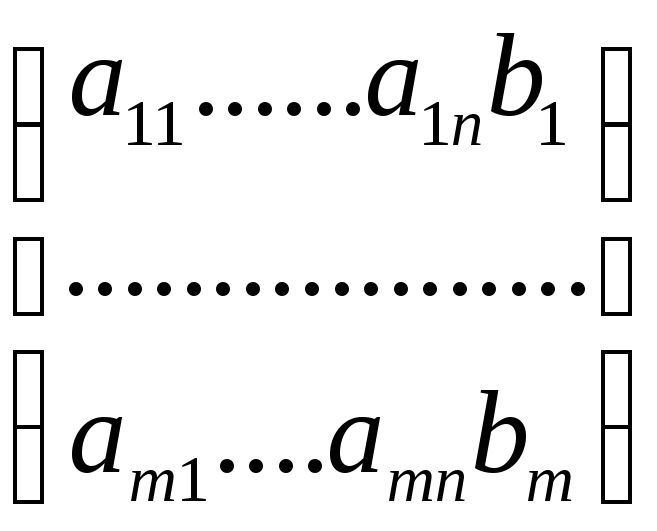и назовём соответственно основной и расширенной матрицами.

Теорема 4.2. (Кронекера-Капелли):

Для того, чтобы система (1) была совместной необходимо и достаточно, чтобы выполнялось равенство

rangA = rangВ.

Алгоритм решения системы:

1. Вычисляют ранги основной и расширенной матриц. Если система совместна, то находят какой-либо базисный минор порядка К.

2. Берётся k уравнений из коэффициентов, которых при неизвестных составлен базисный минор, остальные уравнения отбрасываются. Неизвестные, коэффициенты при которых входят в базисный минор считают главными и оставляют слева, а остальные n-k неизвестных считают свободными и переносят вместе с коэффициентами в правые части уравнений.

3. Методом Гаусса или по правилу Крамера находят выражения главных неизвестных через свободные. Тем самым получают общее решение системы.

4. Придавая свободным неизвестным любые любые числовые значения, находят соответствующие значения главных неизвестных. Тем самым получают частные решения.

Пусть ,,…,- какое-либо решение системы (1). Обозначим

Х =,=,С =

Тогда в матричной форме система (1) запишется так АХ = и, следовательно,АС = В.

Поэтому, если, А- невырожденна, то Х =

Система линейных однородных уравнений

(3)

Теорема 4.3. Для того, чтобы система (3) имела нетривиальное (ненулевое) решение, необходимо и достаточно, чтобы ранг системы (ранг основной матрицы системы) был меньше числа неизвестных.

Следствие 1. Любая система линейных однородных уравнений, в которой число уравнений меньше числа неизвестных, имеет нетривиальное решение.

Следствие 2. Для того чтобы система (3), в которой число уравнений равно числу неизвестных, имела нетривиальное решение, необходимо и достаточно, чтобы её определитель был равен нулю.

Теорема 4.4. Пусть ,,…,-матрицы-столбцы решение системы (3). Тогда с =,,…,(R)- решение (3).

Определение. Фундаментальной системой решений системы (3) называется линейно независимая система решений (матриц-столбцов), через которую линейно выражается любое решение (3).

Теорема 4.5. Пусть k - ранг системы (3), n-число её неизвестных и к < n. Тогда (3) имеет бесконечное множество фундаментальных систем решений, причём каждая из них состоит из (n-к) числа решений.

Правило для нахождения фундаментальной системы решений:

1. Берём любой отличный от нуля определитель d порядка n-k.

2. Свободным неизвестным поочерёдно придаются значения, равные элементам 1-го, 2-го и т.д. столбцов определителя d, и каждый раз из общего решения находят соответствующие значения главных неизвестных.

3. Полученные (n-k) решений составляют фундаментальную систему.