Преобразование координат вектора при переходе от одного базиса к другому.

Пусть в пространстве заданы два базиса

,,…,(“старый”) и,,…,(“новый”).

Тогда x

x =++…+, (1)

x =++…+. (2)

Запишем разложение векторов ,по векторам старого базиса.

= ++…+,

= ++…+, (3)

…

= ++…+.

Матрица

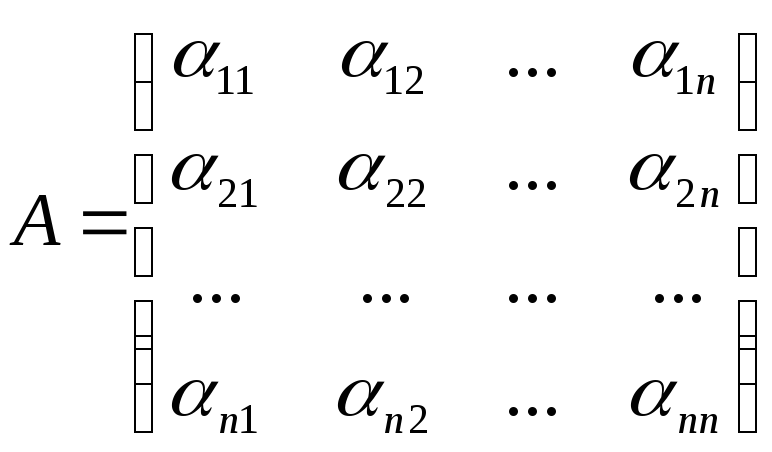–матрица перехода от старого базиса к новому.

Если обозначить матрицы строки

(х) = (,,…,), () = (,,…,), то (х) = ()А.

Теорема 5.2. (об обратной матрице перехода). Матрица перехода от одного базиса к другому всегда имеет обратную.

Так как , то.

Изоморфизм векторных пространств.

Определение. Два векторных пространства V и V’ называются изоморфными (записывается ), если существует такое взаимно однозначное отображениеf из V на V’, что выполняются условия:

, ;

, R,

Теорема 5.3.

Векторные подпространства.

Определение. Непустое множество называется подпространствомV, если выполняются условия:

1)

2) R.

Теорема 5.2. Для любого подпространства U пространства V, где ,ЕслитоU = V.

Сумма и пересечение подпространств.

Определение. Пересечением подпространств и пространстваV называется множество векторов пространства V, каждый из которых принадлежит и(обозначается).

Определение. Суммой подпространств ипространстваV называется множество всех векторов x из V таких, что, где(обозначается).

Лемма 5.2. Пересечение и сумма конечного числа подпространств пространства V является подпространством V.

Лемма 5.3 (о положении базиса). В пространстве любую систему линейно независимых векторов можно дополнить до базиса этого пространства.

Теорема 5.4 (о размерности суммы подпространств). Пусть A и B – подпространства пространства V, тогда

Прямая сумма подпространств.

Определение. Пусть V=и. ТогдаV есть прямая сумма подпространств и(обозначается).

Лемма 5.4. Пусть ,Тогда это разложение единственно.

Лемма 5.5.

Евклидовы пространства.

Определение. Каждой паре векторов поставим в соответствие действительное целое, называемое скалярным произведением векторовa и b, которое удовлетворяет следующим условиям:

1) ;

2) R;

3) ;

4) если .

Тогда V называется евклидовым пространством и обозначается E.

Примеры.

1. с определённым на нём скалярным произведением векторов.

2. Для любых R определим .

3. В пространстве R любых ,.

Определение. Длиной или нормой вектора R называется число

.

Вектор, длина которого равна 1, называется единичным, или нормированным.

Теорема 5.5 (неравенство Коши-Бунявского). Для любых a,bE справедливо неравенство

.

Теорема 5.6 (неравенство треугольников или неравенство Минковского). Для любых a,bE

.

Ортонормированная система векторов.

Определение. Вектора a,bE называются ортогональными (обозначается ), если

Лемма 5.5. (теорема Пифагора). Для любых a,b  E, где

.

Определение. Система векторов пространстваЕ называется ортогональной, если все вектора этой системы попарно ортогональны, т.е.

Теорема 5.7 (о линейной независимости ортогональной системы векторов). Ортогональная система векторов линейно независима.

Теорема 5.8. В любом пространстве Есуществует ортогональный базис.

Следствие. В пространстве Есуществует ортонормированный базис.