
- •А.Д. Ходалевич
- •Комплексные числа. Определение комплексного числа.
- •Действия над комплексными числами.
- •Тригонометрическая форма комплексного числа.
- •Извлечение корня из комплексного числа.
- •Многочлены и их корни. Операции над многочленами
- •Деление многочленов.
- •Наибольший общий делитель.
- •Корни многочлена.
- •Основная теорема алгебры.
- •Следствия из основной теоремы.
- •Многочлены с действительными коэффициентами.
- •Рациональные дроби.
- •Многочлены с рациональными коэффициентами.
- •Матрицы и определители.
- •Свойства определителей.
- •Ранг матрицы.
- •Операции над матрицами.
- •Обратная матрица
- •Системы линейных уравнений
- •Линейные (векторные) пространства.
- •Линейная зависимость и независимость векторов.
- •Преобразование координат вектора при переходе от одного базиса к другому.
- •Изоморфизм векторных пространств.
- •Векторные подпространства.
- •Сумма и пересечение подпространств.
- •Прямая сумма подпространств.
- •Евклидовы пространства.
- •Ортонормированная система векторов.
- •Ортогональное дополнение пространства.
- •Линейные операторы и действия над ними.
- •Действия с линейными операторами.
- •Обратный оператор. Ядро и образ линейного оператора.
- •Матрица линейного оператора.
- •Собственные числа и собственные вектора линейного оператора.
- •Линейные операторы в Евклидовом пространстве. Ортогональный оператор.
- •Самосопряжённый (симметрический) оператор.
- •Квадратичные формы. Приведение квадратичной формы к каноническому виду.
- •Нормальный вид квадратичной формы
- •Знакоопределенные квадратичные формы
- •Алгебраические структуры.
- •Примеры подгруппы
- •Изоморфизм групп
- •Теорема Лагранжа
- •Циклические группы
- •Нормальная подгруппа. Фактор группа.
- •Гомоморфизм групп
- •Литература:
- •«Алгебра» Тексты лекций
- •246019, Г. Гомель, ул. Советская, 104
- •246019, Г. Гомель, ул. Советская, 104
Линейные (векторные) пространства.
Определение. Линейным (векторным) пространством называют непустое множество V с заданными на нём операциями сложения и умножения на число, которое удовлетворяет следующим условиям:
x + y = y + x ,
 x,y
x,y V;
V;(x + y) + z = x + (y + z),
 x,y,z
x,y,z V;
V; e
e
 V,
что
V,
что x
x V
V
x + e = e + x = x, (e-нулевой элемент);
4.
![]() x
x
![]() V,
V,
![]() y
(противоположный к x),
что
y
(противоположный к x),
что
x + y = e;
5.
![]() (
(![]() x)
= (
x)
= (![]()
![]() )x
,
)x
,
![]()
![]() ,
,![]()
![]() C,
C,
![]() x
x![]() V
;
V
;
6. 1x = x;
7. (x
+
y)
=
![]() x
+
x
+![]() y;
y;
![]() x,
y
x,
y![]() V,
V,
![]()
![]()
![]() C;
C;
8. (![]() +
+![]() )
x
=
)
x
=
![]() x
+
x
+![]() x,
x,
![]() x
x![]() V,
V,
![]()
![]() ,
,
![]()
![]() C;
C;
В дальнейшем под числами будем понимать только действительные числа. Тогда V – линейное пространство, в дальнейшем просто пространство, над множеством (полем) действительных чисел. Элементы пространства называются векторными.
Нулевой вектор
обозначается как
![]() ,
а противоположный кх
как (-х).
Для сокращения записи, в дальнейшем, V
–
векторное
пространство.
,
а противоположный кх
как (-х).
Для сокращения записи, в дальнейшем, V
–
векторное
пространство.
Примеры.
Множество
 (
(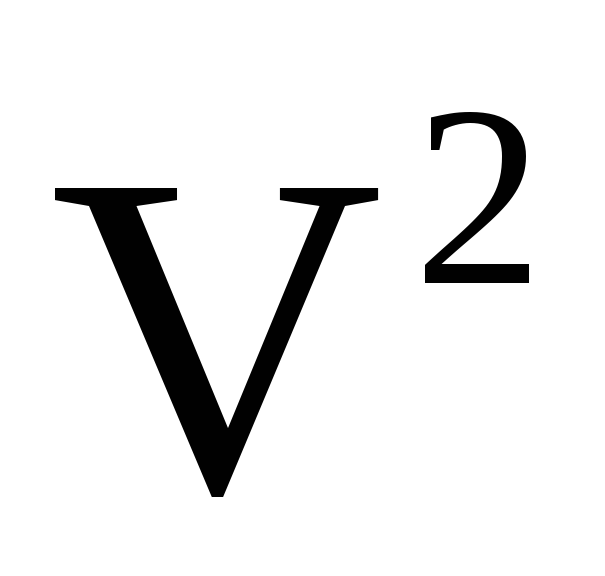 )
всех геометрических векторов в
пространстве (на плоскости)- векторное
пространство над R
относительно
линейных операций над векторами.
)
всех геометрических векторов в
пространстве (на плоскости)- векторное
пространство над R
относительно
линейных операций над векторами.На множестве
![]() = {
= {![]() ,
,![]() ,...,
,...,![]() |
|![]()
![]() R}.
R}.
Введём операции
![]() х
= (
х
= (![]() ,
,![]() ,...,
,...,![]() )
и
)
и
![]() у
= (
у
= (![]() ,
,![]() ,...,
,...,![]() )
)
x +
y =
(![]() +
+![]() ,
,![]() +
+![]() ,…,
,…,![]() +
+![]() )
)
![]()
![]()
![]() R,
R,
![]() x=
(
x=
(![]()
![]() ,
,![]()
![]() ,...,
,...,![]()
![]() )
)
Тогда
![]() -
векторное пространство.
-
векторное пространство.
Множество М (n,R) всех квадратных матриц n-го порядка с действительными элементами и операциями сложения матриц и умножения на число является векторным пространством.
Множество R[a,b] всех непрерывных на отрезке [a,b]функций с операциями сложения функций и умножения функции на число – векторное пространство.
Множество
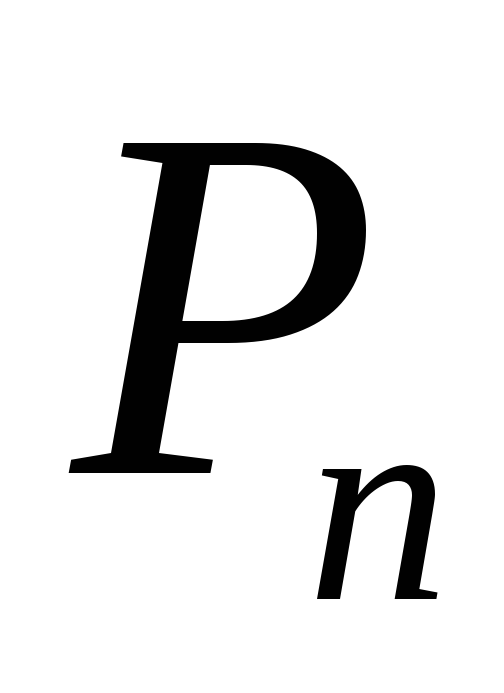 [х]
всех многочленов переменной х степени,
не превосходящей n,
является векторным пространством.
[х]
всех многочленов переменной х степени,
не превосходящей n,
является векторным пространством.Нулевое векторное пространство, т.е. пространство, состоящее только из нулевых векторов: {
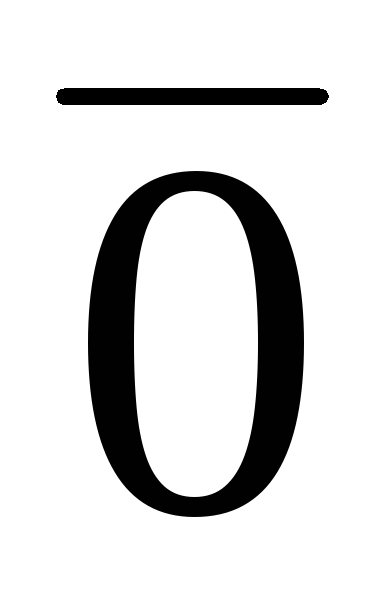 }.
}.Множество С – векторное пространство называется множеством действительных чисел.
Лемма 5.1.
В V существует единственный нулевой элемент
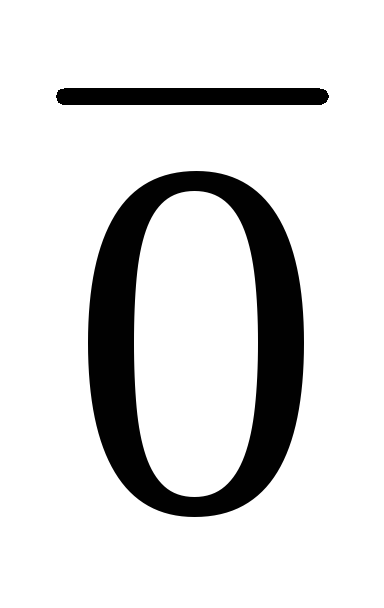 ;
; x
x V,
существует единственный противоположный
к х;
V,
существует единственный противоположный
к х; x
x V,
0х =
V,
0х =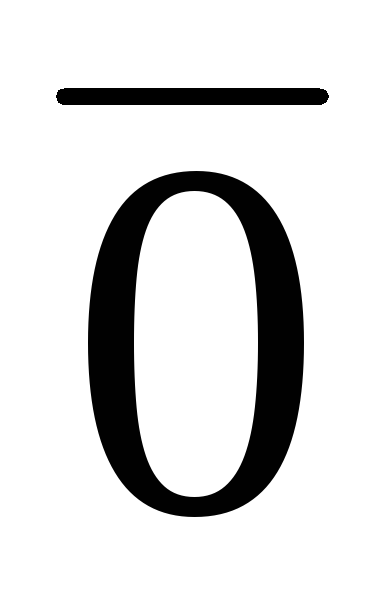 ;
;

 R,
R,
 0
=
0
=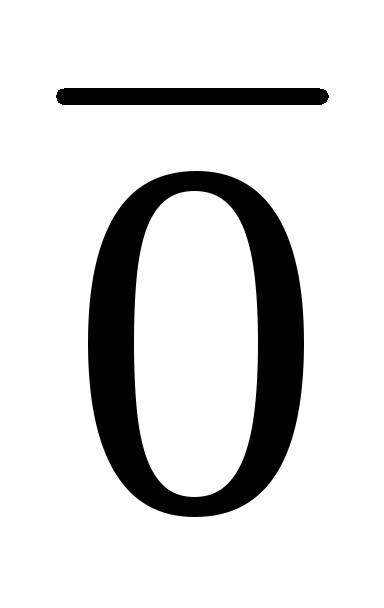 ;
;Если
 х
=
х
=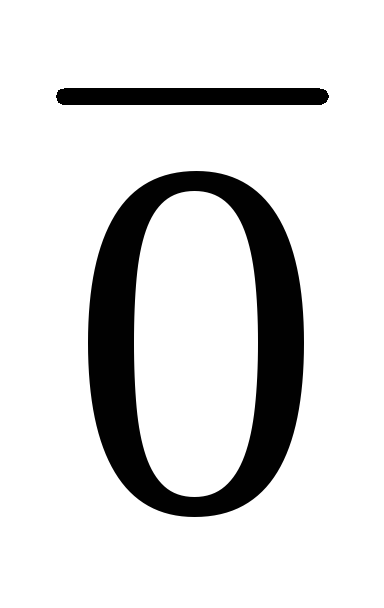 ,
то либо
,
то либо =
0 либо х =
=
0 либо х =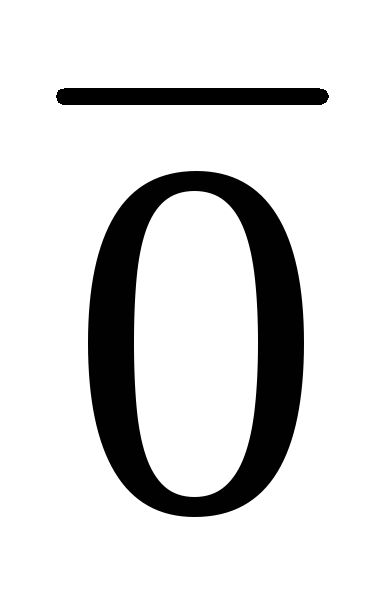 ;
; x
x V,
(-1)х = -х;
V,
(-1)х = -х;
Линейная зависимость и независимость векторов.
Определение.
Конечная система векторов
![]() ,
,![]() ,…,
,…,![]() пространстваV
называется линейно
зависимой,
если найдутся такие числа
пространстваV
называется линейно
зависимой,
если найдутся такие числа
![]() ,
,![]() ,…,
,…,![]() не равные одновременно нулю, что имеет
место равенство
не равные одновременно нулю, что имеет
место равенство
![]()
![]() +
+![]()
![]() +…+
+…+![]()
![]() =
=![]() .
.
В противном случае система векторов называется линейно независимой.
Выражение вида
![]()
![]() +
+![]()
![]() +…+
+…+![]()
![]() называетсялинейной
комбинацией
векторов
называетсялинейной
комбинацией
векторов
![]() ,
,![]() ,…,
,…,![]() .
.
Определение.
Система
векторов
![]() ,
,![]() ,…,
,…,![]() называетсябазисом
пространства V,
если:
называетсябазисом
пространства V,
если:
эта система линейно независима;
 x
x V,
х =
V,
х =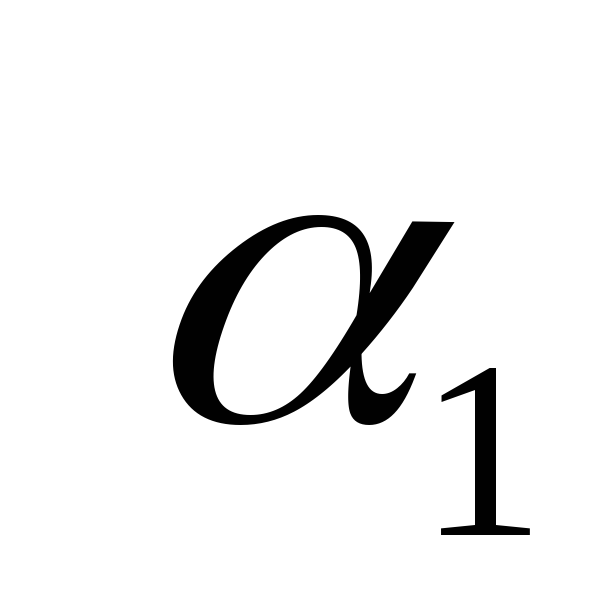
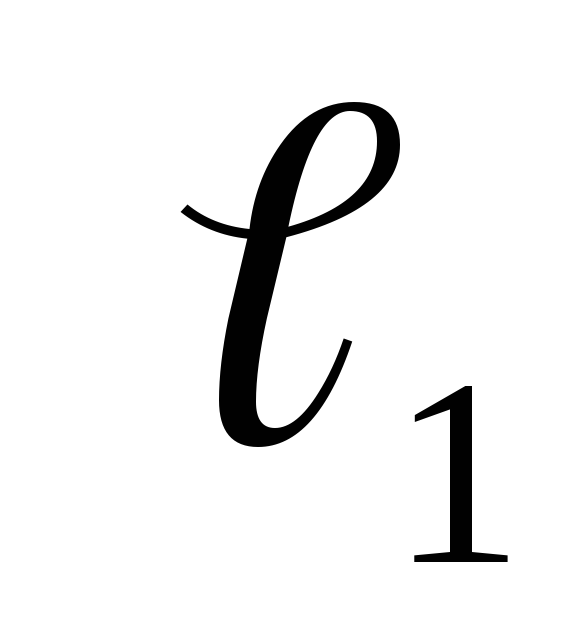 +
+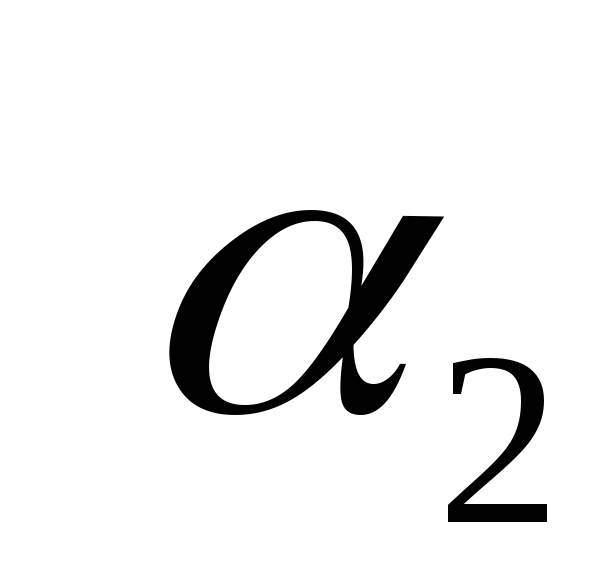
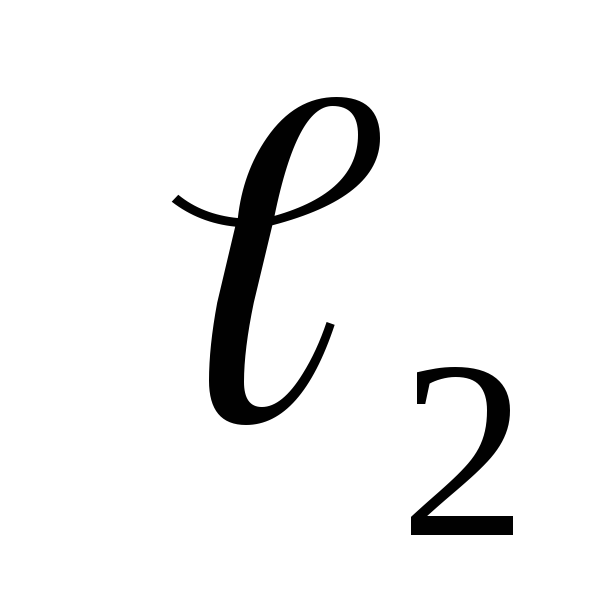 +…+
+…+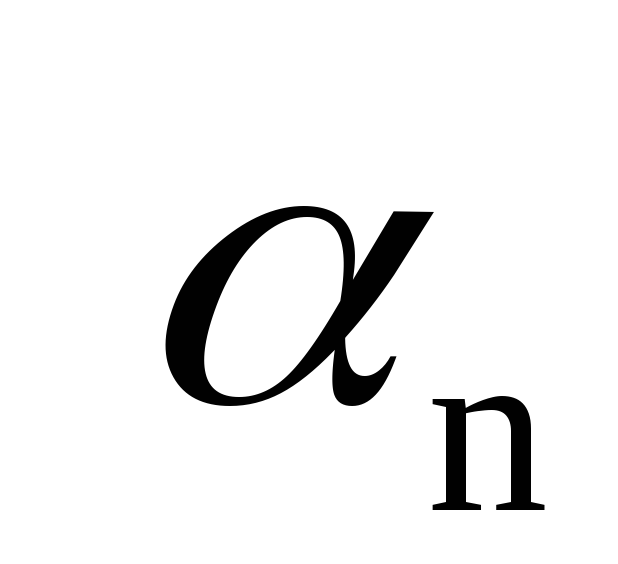
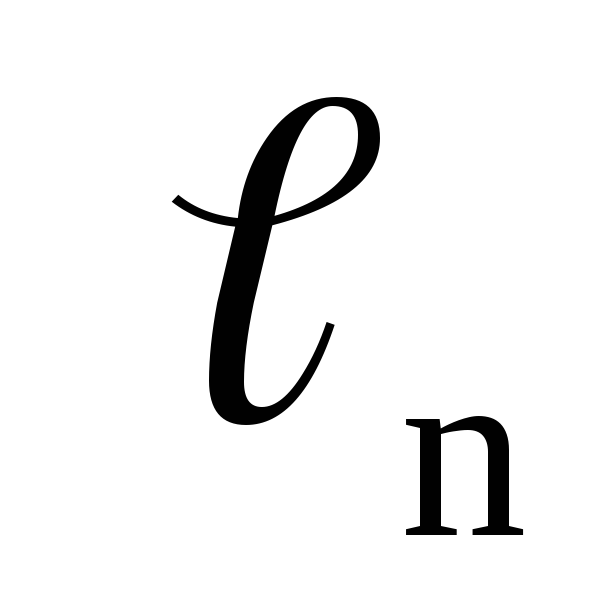 .
.
Определение.
Число n
называется размерностью пространства
V,
если в этом пространстве существует n
линейно независимых векторов, а любые
n
+ 1 векторов- линейно зависимы. В этом
случае пишут dimV
= n
и обозначают
![]() .
.
Теорема 5.1. (о базисе). В пространстве V размерности n любая система состоящая из n линейно независимых векторов образует базис.
Если
![]() ,
,![]() ,…,
,…,![]() –
базисV,
то
–
базисV,
то
![]() x
x![]() V
х
=
V
х
=![]()
![]() +
+![]()
![]() +…+
+…+![]()
![]() –разложение
вектора х
по векторам
базиса.
–разложение
вектора х
по векторам
базиса.
В этом случае числа
![]() ,
,![]() ,…,
,…,![]() называютсякоординатами
вектора х в базисе
называютсякоординатами
вектора х в базисе
![]() ,
,![]() и пишут
и пишут
х
= (![]() ,
,![]() ,…,
,…,![]() ).
).
