Извлечение корня из комплексного числа.

Корнем n-ой степени (n  N) из комплексного числа называется комплексное число, для которого(обозначается).

Сравнивая модули и аргументы в последнем равенстве, получаем формулу нахождения всех корней n-ой степени из комплексного числа Z:

, где k = 0, 1, …, n – 1.

Вывод: существует ровно n различных значений корня n-ой степени из комплексного числа.

Если Z = 1, то и,k = 0, …, n – 1.

Корень n-ой степени из 1 называется первообразным, если он не является корнем из 1 с меньшим, чем n натуральным показателем.

Свойства:

Пусть Z₁ и Z₂ – корни n-ой степени из 1. Тогда:

1. Z₁ ∙ Z₂ – корень n-ой степени из 1;

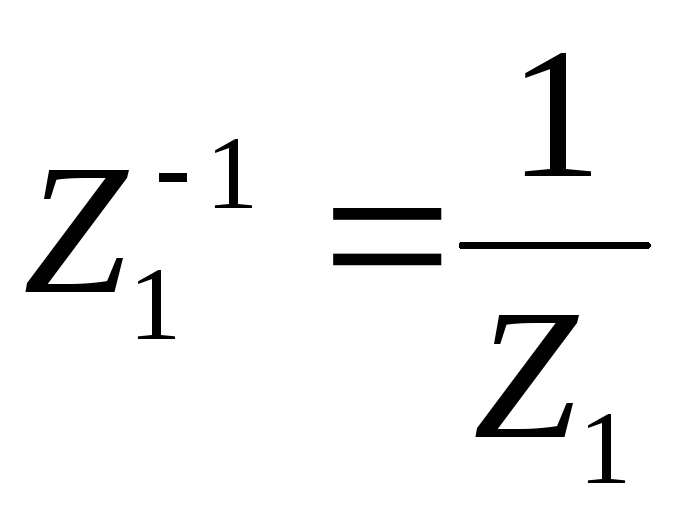2. –корень n-ой степени из 1.

Многочлены и их корни. Операции над многочленами

Определение. Многочленом (полиномом) n-ой степени от неизвестного x называется выражение вида

, где a_i  C, n – целое неотрицательное число.

Числа a_i – коэффициенты многочлена, a₀ и a_n – соответственно старший коэффициент и свободный член. Считаем, что a₀  0.

Два многочлена f(x) и g(x) одинаковой степени называют равными, если равны их коэффициенты при одинаковых степенях неизвестного (пишут f(x) = g(x)).

Многочлен нулевой степени – это любое отличное от нуля комплексное число. Число нуль – многочлен, степень которого не определена.

Пусть

Тогда сумма многочленов f(x) и g(x) есть многочлен

, где C_i = a_i + b_i и либо k = n, либо k = m.

Произведением многочленов f(x) и g(x) называется многочлен

, где ,i = 0, 1, …, , .

Вычитание многочленов определяется как операция, обратная операции сложения. В этом случае противоположным к f(x) является

.

Для умножения многочленов обратная операция не существует, то есть, нет такого многочлена g(x), что .

Деление многочленов.

Обозначим степень ненулевого многочлена f(x) через .

Теорема 2.1. (о делении с остатком). Для любых двух многочленов f(x) и g(x) существуют такие единственные многочлены q(x) и r(x), что

и или же.

Многочлены q(x) и r(x) называются соответственно частным и остатком от деления f(x) на g(x). Тогда f(x) делится на g(x) или g(x) делит f(x), если остаток ().

Следствие 2.1.1. g(x) является делителем f(x) тогда и только тогда, когда существует многочлен (x) такой, что .

Свойства делимости:

1. Если f(x) делится на g(x), а g(x) делится на (x), то f(x) делится на (x).

2. Если f(x) и g(x) делится на (x), то их сумма и разность делится на (x).

3. Если f(x) делится на (x), то для любого g(x) на (x) делится и .

4. Если f_i(x) делится на (x) для любого , то на(x) делится и многочлен

, где g_i(x) – произвольные многочлены.

5. Любой многочлен f(x) делится на многочлен нулевой степени.

6. Если f(x) делится на g(x), то f(x) делится на ag(x), где ,.

7. Пусть f(x) делится на g(x). Тогда и только тогда , когда, где,.

8. f(x) делится на g(x) тогда и только тогда, когда af(x) делится на g(x) ,.

Наибольший общий делитель.

Определение. Многочлен d(x) называется общим делителем многочленов f(x) и g(x), если он является делителем каждого из них.

Наибольшим общим делителем отличным от нуля многочленов f(x) и g(x) называется такой их общий делитель d(x), который, вместе с тем, сам делится на любой другой общий делитель этих многочленов. Обозначается НОД или (f(x), g(x)).

Если , тоf(x) и g(x) называются взаимно обратными.

Метод последовательного деления или алгоритм Евклида заключается в следующей схеме:

…………………….

где

Теорема 2.2. НОД (f(x), g(x)), где f(x) и g(x) – ненулевые, равен последнему отличному от нуля остатку в алгоритме Евклида, если g(x) не делит f(x), и совпадает с g(x) в противном случае.

Из свойств делимости следует, что НОД (f(x), g(x)) определен лишь с точностью до множителя нулевой степени. Таким образом f(x) и g(x) взаимно простые тогда и только тогда, когда НОД (f(x), g(x)) = 1.

Теорема 2.3. Пусть . Тогда существуют такие многочленыu(x) и v(x), что выполняется равенство

.

Причем, если степени f(x) и g(x) больше нуля, то и.

Следствие 2.3.1. (критерий взаимной простоты). f(x) и g(x) взаимно просты тогда и только тогда, когда существуют u(x) и v(x) такие, что

.

Теорема 2.4.

1. Если f(x) взаимно прост с (x) и h(x), то он взаимно просто с их произведением.

2. Если f(x)∙g(x) делится на (x), но f(x) и g(x) – взаимно просты, то g(x) делится на (x).

3. Если f(x) делится на g(x) и h(x), и g(x) и h(x) взаимно просты, то f(x) делится на g(x)∙h(x).

Теорема 2.5. Пусть f₁(x), …, f_n(x) – ненулевые и пусть

, , …,. Тогда– НОД этих многочленов.