
- •А.Д. Ходалевич
- •Комплексные числа. Определение комплексного числа.
- •Действия над комплексными числами.
- •Тригонометрическая форма комплексного числа.
- •Извлечение корня из комплексного числа.
- •Многочлены и их корни. Операции над многочленами
- •Деление многочленов.
- •Наибольший общий делитель.
- •Корни многочлена.
- •Основная теорема алгебры.
- •Следствия из основной теоремы.
- •Многочлены с действительными коэффициентами.
- •Рациональные дроби.
- •Многочлены с рациональными коэффициентами.
- •Матрицы и определители.
- •Свойства определителей.
- •Ранг матрицы.
- •Операции над матрицами.
- •Обратная матрица
- •Системы линейных уравнений
- •Линейные (векторные) пространства.
- •Линейная зависимость и независимость векторов.
- •Преобразование координат вектора при переходе от одного базиса к другому.
- •Изоморфизм векторных пространств.
- •Векторные подпространства.
- •Сумма и пересечение подпространств.
- •Прямая сумма подпространств.
- •Евклидовы пространства.
- •Ортонормированная система векторов.
- •Ортогональное дополнение пространства.
- •Линейные операторы и действия над ними.
- •Действия с линейными операторами.
- •Обратный оператор. Ядро и образ линейного оператора.
- •Матрица линейного оператора.
- •Собственные числа и собственные вектора линейного оператора.
- •Линейные операторы в Евклидовом пространстве. Ортогональный оператор.
- •Самосопряжённый (симметрический) оператор.
- •Квадратичные формы. Приведение квадратичной формы к каноническому виду.
- •Нормальный вид квадратичной формы
- •Знакоопределенные квадратичные формы
- •Алгебраические структуры.
- •Примеры подгруппы
- •Изоморфизм групп
- •Теорема Лагранжа
- •Циклические группы
- •Нормальная подгруппа. Фактор группа.
- •Гомоморфизм групп
- •Литература:
- •«Алгебра» Тексты лекций
- •246019, Г. Гомель, ул. Советская, 104
- •246019, Г. Гомель, ул. Советская, 104
МИНИСТЕРСТВО ОБРАЗОВАНИЯ
РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования «Гомельский
государственный университет
имени Франциска Скорины»
А.Д. Ходалевич
Р.В. Бородич
В.Н. Рыжик
«Алгебра»
Тексты лекций
Гомель, 2004
УДК 512 (078)
ББК 22.14 Я73
Х 69
Рецензенты: Семенчук В.Н. – доктор физико-математических наук
кафедра высшей математики учреждения образования «Гомельский государственный университет имени Франциска Скорины».
Рекомендован к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины» 24 марта 2004 года, протокол № 7
Ходалевич А.Д.
Х 69 Алгебра: Курс лекций. /А.Д.Ходалевич, Р.В.Бородич, В.Н.
Рыжик. − Гомель: УО «ГГУ им. Ф.Скорины», 2004. − 37с.
Дается краткое изложение курса лекций по алгебре для студентов, обучающихся по специальности «Прикладная математика»
УДК 512 (078)
ББК 22.14 Я73
Х 69
© А.Д. Ходалевич, Р.В. Бородич, В.Н. Рыжик 2004
© Учреждение образования «Гомельский государственный университет имени Франциска Скорины», 2004
СОДЕРЖАНИЕ
1. Комплексные числа……………………………………………4
2. Многочлены и их корни……………………………………….6
3. Матрицы и определители……………………………………..12
4. Системы линейных уравнений………………………………..16
5. Линейные (векторные) пространства…………………………19
6. Квадратичные формы……………………………………….….29
7. Алгебраические структуры………………………………….…32
Литература…………………………………………………………37
Комплексные числа. Определение комплексного числа.
Определение. Комплексным числом Z называется выражение вида a + bi, где a, b – действительные числа, символ i удовлетворяет условию i2 = –1.
Число a – действительная часть, bi – мнимая часть, i – мнимая единица комплексного числа.
Множество всех комплексных чисел обозначается С. Таким образом, R C.
Число bi называется чисто мнимым.
Комплексные числа Z1 = a1 + b1i и Z2 = a2 + b2i называются равными (пишут Z1 = Z2), если a1 = a2 и b1 = b2.
Число Z = 0 + 0i называется нулем и обозначается 0 R.
Числа вида a
+ bi
и
a
– bi
называются комплексно-сопряженными
и обозначаются соответственно Z
и
![]() .
.
О чевидно,
что каждому комплексному числуZ
= a
+ bi
соответствует единственная точка (a;
b)
координатной плоскости 0XY.
Справедливо и обратное утверждение.
Плоскость OXY
называется
комплексной,
оси OX
и OY
называются соответственно действительной
и
мнимой.
чевидно,
что каждому комплексному числуZ
= a
+ bi
соответствует единственная точка (a;
b)
координатной плоскости 0XY.
Справедливо и обратное утверждение.
Плоскость OXY
называется
комплексной,
оси OX
и OY
называются соответственно действительной
и
мнимой.
Действия над комплексными числами.
Пусть даны два комплексных числа Z1 = a1 + b1i и Z2 = a2 + b2i.
Суммой Z1 и Z2 называется комплексное число Z = Z1 + Z2 = (a1 + a2) + (b1 + b2)i.
Разность – это комплексное число Z = Z1 – Z2 = (a1 – a2) + (b1 – b2)i.
Произведения комплексных чисел Z1 и Z2 называется комплексное число Z = Z1 ∙ Z2 = (a1a2 – b1b2) + (a1b2 + a2b1)i.
Для нахождения
частного
![]() знаменатель и числитель умножают на
знаменатель и числитель умножают на![]() .
Тогда
.
Тогда
![]() .
.
n-ой
степенью
комплексного числа Z
(n
N)
называется комплексное число
![]() .
.
Лемма 1.1.
![]() ;
;![]() .
.
Тригонометрическая форма комплексного числа.
Пусть Z
= x
+ yi
и даны прямоугольные прямоугольная и
полярная системы координат. Тогда
![]() ,
,![]() и следовательно,
и следовательно,![]() –тригонометрическая
форма
комплексного числа.
–тригонометрическая
форма
комплексного числа.
![]()
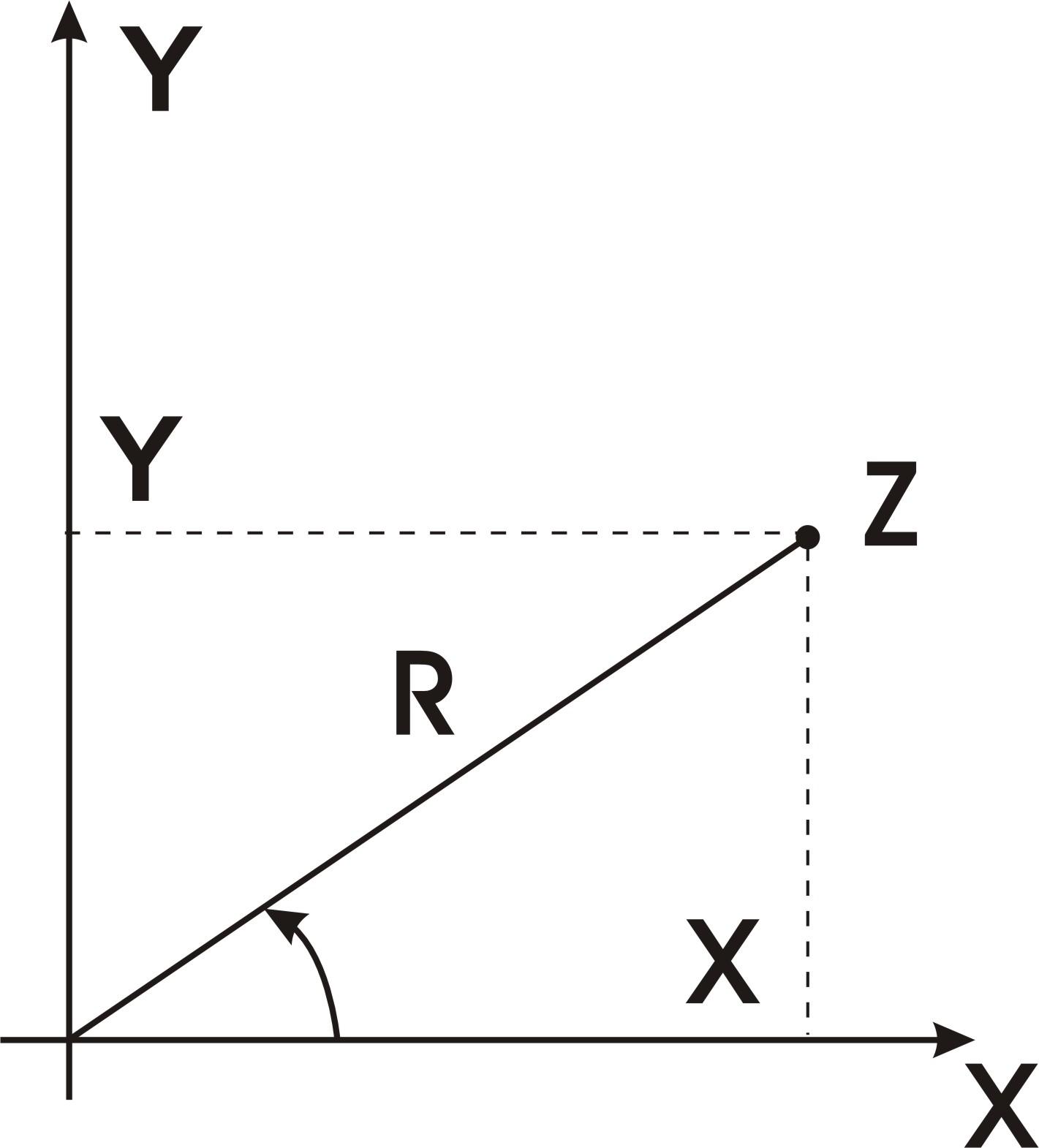 –модуль
комплексного числа Z
и обозначается
|Z|.
А полярный угол
- аргумент и обозначается
–модуль
комплексного числа Z
и обозначается
|Z|.
А полярный угол
- аргумент и обозначается
![]() .
.
Запись Z = x + yi называется алгебраической формой комплексного числа. Переход от алгебраической формы к тригонометрической осуществляется по формулам
![]() ;
;
![]() .
.
Пусть даны два
комплексных числа
![]() ;
;![]() .
.
Тогда
![]()
![]() .
.
Аналогично
![]() .
.
Индукцией по числу
K
Z
получаем
![]() .
.
В частности,
![]() –формула
Муавра.
–формула
Муавра.
