
- •Содержание
- •1 Роль и место понятия «площадь в школьном» курсе математики
- •2 Методика изучения данной темы
- •2.1 Знакомство с понятием площади
- •2.2 Площадь прямоугольника
- •2.3 Площадь параллелограмма
- •2.4 Площадь треугольника
- •2.5 Площадь круга
- •2.6 Площадь произвольного n-угольника
- •2.7 Площадь правильного n-угольника
- •3 Задачи планиметрии из централизованного тестирования
- •4 Задачи и упражнения для самостоятельного решения
2.7 Площадь правильного n-угольника
Вывод
площади правильного n-угольника
связан с радиусом вписанной в этот
n-угольник
окружности и радиусом окружности,
описанной около него. При выводе этой
формулы используется разбиение
n-угольника
на n
треугольников. Если
 – площадь данного правильного
многоугольника, а – его сторона,
– площадь данного правильного
многоугольника, а – его сторона, – периметр, а
– периметр, а и
и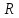 – радиусы соответственно вписанной и
описанной окружностей, то
– радиусы соответственно вписанной и
описанной окружностей, то .
Докажем это: Соединив центр данного
многоугольника с его вершинами, как
показано на рисунке 2.7.1, мы разобьем его
наn
равных треугольников, площадь каждого
из которых равна
.
Докажем это: Соединив центр данного
многоугольника с его вершинами, как
показано на рисунке 2.7.1, мы разобьем его
наn
равных треугольников, площадь каждого
из которых равна
 .
Следовательно,
.
Следовательно, .
Далее
.
Далее ,
, .
[11,c.
174]
.
[11,c.
174]

Рисунок 2.7.1
Рисунок 2.7.1
Пример 2.7.1.
Данный квадрат со стороной a срезан по углам так, что образовался правильный восьмиугольник. Определить площадь этого восьмиугольника.
Решение:
Пусть
 (рисунок 2.7.2). Тогда
(рисунок 2.7.2). Тогда
 или
или ,
откуда
,
откуда

Рисунок 2.7.2
Следовательно, искомая площадь

Ответ:
Пример 2.7.2.
Вся дуга окружности радиуса R разделена на четыре большие и четыре малые части, которые чередуются одна за другой. Большая часть в 2 раза длиннее малой. Определить площадь восьмиугольника, вершинами которого являются точки деления дуги окружности.
Решение:
Пусть
малая дуга содержит
 градусов. Тогда
градусов. Тогда ,
откуда
,
откуда
 Значит, восьмиугольник содержит четыре
треугольника с центральным углом
Значит, восьмиугольник содержит четыре
треугольника с центральным углом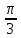 (их суммарная площадь
(их суммарная площадь )
и четыре треугольника с центральным
углом
)
и четыре треугольника с центральным
углом (их суммарная площадь
(их суммарная площадь ).
Искомая площадь составляет
).
Искомая площадь составляет
Ответ:
Пример 2.7.3.
Дан
квадрат со стороной .
На каждой стороне квадрата вне его
построена трапеция так, что верхние
основания этих трапеций и их боковые
стороны образуют правильный
двенадцатиугольник. Вычислить его
площадь.
.
На каждой стороне квадрата вне его
построена трапеция так, что верхние
основания этих трапеций и их боковые
стороны образуют правильный
двенадцатиугольник. Вычислить его
площадь.
Решение:
Искомая
площадь
 ,
где
,
где
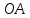 и
и –
радиусы окружности, описанной около
квадрата и двенадцатиугольника (рисунок
2.7.3). Так как сторона квадрата равна
–
радиусы окружности, описанной около
квадрата и двенадцатиугольника (рисунок
2.7.3). Так как сторона квадрата равна
 ,
то
,
то .
Имеем
.
Имеем где
где ⏊
⏊ Но
Но
 ,
поскольку
,
поскольку
 .
Таким образом,
.
Таким образом,
 ,
то есть
,
то есть

Рисунок 2.7.3
Ответ:

3 Задачи планиметрии из централизованного тестирования
2004
Вариант 1
В8.
В равнобедренном треугольнике
 через вершины основания
через вершины основания и
и и точку
и точку (
( лежит
на высоте, проведённой к основанию, и
делит её в отношении
лежит
на высоте, проведённой к основанию, и
делит её в отношении ,считая
от основания) проведены прямые
,считая
от основания) проведены прямые и
и (D
(D
 AB;
E
AB;
E
 AC).
Найдите площадь треугольника
AC).
Найдите площадь треугольника
 ,
если площадь трапеции
,
если площадь трапеции равна
64. [12,c.64]
равна
64. [12,c.64]
Решение:

Введём
обозначения:


Из
рисунка следует, что
 Отсюда
Отсюда


Составляем систему:

Рисунок 3.1
Из
системы получаем:
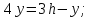
Решая
это уравнение найдём
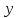 :
:


Подставляем во второе уравнение системы, получаем:


Найдём
площадь треугольника




Ответ:
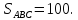
2005
Вариант 1
А8.
В равнобедренном треугольнике
 со сторонами
со сторонами и
и проведена
высота
проведена
высота к боковой стороне. Если
к боковой стороне. Если и
и – центры окружностей, описанных около
треугольников
– центры окружностей, описанных около
треугольников и
и ,
то расстояние между точками
,
то расстояние между точками и
и равно…[13,c.
80]
равно…[13,c.
80]
Решение:
В
условии задачи
не
сказано конкретно, чему равны боковые
стороны
 и
и
 и основание
и основание .
Если
.
Если ,
а
,
а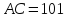 ,
то не будет выполняться неравенство
треугольника
,
то не будет выполняться неравенство
треугольника .
Поэтому
.
Поэтому ,
а
,
а .
Далее нужно вспомнить тот факт, что
центр окружности, описанной около
прямоугольного треугольника, лежит на
середине гипотенузы. Поэтому центры
окружностей, описанных около треугольников
.
Далее нужно вспомнить тот факт, что
центр окружности, описанной около
прямоугольного треугольника, лежит на
середине гипотенузы. Поэтому центры
окружностей, описанных около треугольников и
и
 ,
точки
,
точки
 и
и
 –
соответственно середины сторон
–
соответственно середины сторон
 и
и .
.
B

О2
Н

А С
О1
Рисунок 3.2
Таким
образом,
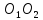 –
средняя
линия треугольника
–
средняя
линия треугольника
 и
и
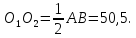
Ответ:
2006
Вариант 1
B4.
Четырёхугольник
 вписан в окружность. Если
вписан в окружность. Если ,
, ,
, ,
то градусная мера угла между прямыми
,
то градусная мера угла между прямыми и
и равна…[14,c.
63]
равна…[14,c.
63]
Решение:
Так
как по условию нам дано, что
 ,
, ,
, ,
то
,
то
 Тогда
Тогда Нам известно, что четырёхугольник можно
вписать в окружность тогда и только
тогда, когда суммы его противоположных
углов равны
Нам известно, что четырёхугольник можно
вписать в окружность тогда и только
тогда, когда суммы его противоположных
углов равны Значит,
Значит,

Рисунок 3.3
А
из этого следует, что
 Из треугольника
Из треугольника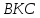 можно найти угол, который нам и нужен.
Итак,
можно найти угол, который нам и нужен.
Итак, Получаем, что
Получаем, что
Ответ:

2007
Вариант 1
А12. Большее основание трапеции равно 114. Найдите меньшее основание трапеции, если расстояние между серединами её диагоналей равно 19. [15, c. 62]
Решение:
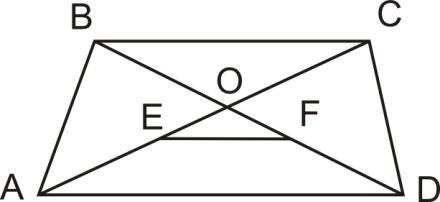
Рисунок 3.4
Обозначим
меньшее основание трапеции
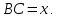


Треугольники
 и
и
 подобны. Получаем соотношение:
подобны. Получаем соотношение:
Из
подобия треугольников
 получаем:
получаем:

Разделим второе уравнение на первое:


Следовательно:



Получаем,
что меньшее основание трапеции равно

Ответ:

2008
Вариант 1
А11.
Параллельно стороне
 треугольника
треугольника проведена прямая, пересекающая сторону
проведена прямая, пересекающая сторону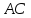 в точке
в точке так, что
так, что .
Если площадь треугольника
.
Если площадь треугольника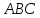 равна 50, то площадь получившейся трапеции
равна…[16,c.
72]
равна 50, то площадь получившейся трапеции
равна…[16,c.
72]
Решение:

Рисунок 3.5
Пусть
 Из
условия нам дано, что
Из
условия нам дано, что

Отсюда
 Тогда,
Тогда, Следовательно,
Следовательно, Теперь найдём площадь трапеции
Теперь найдём площадь трапеции
 Получаем, что
Получаем, что
Ответ:

2009
Вариант 1
А13. Высота прямоугольного треугольника, проведённая к гипотенузе, делит её на отрезке, длины, которых относятся как 1:4. Если высота равна 8, то гипотенуза равна…[17, c. 72]
Решение:
Длина
высоты прямоугольного треугольника,
проведенной к гипотенузе, может быть
найдена по формуле:

B

K
A C
Рисунок 3.6
По
условию нам дано, что
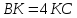 .
Значит,
.
Значит,

Отсюда
получаем, что
 .
Тогда
.
Тогда

Ответ:

2010
Вариант 1
А12.
Величины двух углов треугольника равны
 и
и ,
а высота, проведённая из вершины большего
угла, равна 9. Найдите меньшую сторону
треугольника.
,
а высота, проведённая из вершины большего
угла, равна 9. Найдите меньшую сторону
треугольника.
Решение:

Рисунок 3.7
Пусть
 ,
значит
,
значит
 Так как
Так как –
–
высота
треугольника
 ,
то
,
то
 .
Поскольку треугольник
.
Поскольку треугольник прямоугольный, то катет прямоугольного
треугольника, лежащий против угла в 30,
равен половине гипотенузы.
прямоугольный, то катет прямоугольного
треугольника, лежащий против угла в 30,
равен половине гипотенузы.
Из
свойства получаем:
 Значит,
Значит,
Ответ:
2011
Вариант 1
А16.
В ромб площадью
 вписан круг площадью
вписан круг площадью
 .
Сторона ромба равна…
.
Сторона ромба равна…
Решение:
 ;
;
 ;
;
 ;
;
 .
.
Так
как площадь ромба по условию равна
 ,
то
,
то Тогда,
Тогда,
 Отсюда
получаем, что
Отсюда
получаем, что

Рисунок 3.8
Ответ:

2012
Вариант 1
А11.
Четырёхугольник
 ,
в котором
,
в котором ,
вписан в окружность. Найдите градусную
меру угла
,
вписан в окружность. Найдите градусную
меру угла .
.
Решение:

Четырёхугольник
можно вписать в окружность тогда и
только тогда, когда суммы его противоположных
углов равны

Значит,
Рисунок 3.9
Ответ:

2013
Вариант 1
В3.
Основание остроугольного равнобедренного
треугольника равно 10, а синус противолежащего
угла равен
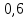 .
Найдите площадь треугольника.
.
Найдите площадь треугольника.
Решение:

Рисунок 3.10
1.
Найдём косинус угла по формуле
по формуле
 ,
отсюда
,
отсюда

Так
как угол
 −
острый, то выбираем знак «
−
острый, то выбираем знак « »:
»:
 .
.
2.
Для нахождения длины боковой стороны
 (рисунок 3.10) применим теорему косинусов:
(рисунок 3.10) применим теорему косинусов:
 или
или
 или
или
 или
или или
или
3.
Находим площадь треугольника
 по формуле:
по формуле:
 ;
;

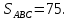
Ответ:
 .
.
2014
Вариант 1
Задача В3. В окружность радиусом 6 вписан треугольник, длины двух сторон которого равны 6 и 10. Найдите длину высоты треугольника, проведенной к его третьей стороне.
Решение:
Выполним
вспомогательный чертеж для решения
задачи. Пусть
 – заданный треугольник, у которого
– заданный треугольник, у которого .
.
Проведем
высоту
 треугольника.
треугольника.

Рисунок 3.11
В подобных задачах самый сложный момент ─ это понять, как связать параметры треугольника (углы или стороны) с параметрами окружности. Ведь задачу мы решаем про треугольник, однако, поскольку дан радиус описанной окружности, то это нужно как-то использовать для получения недостающих сведений о самом треугольнике.
Одна
из самых известных связей между
треугольником и описанной окружностью
доказывается в теореме синусов. Запишем
выводы этой теоремы для угла
 :
:

Здесь
 – радиус описанной около треугольника
окружности. Отсюда получаем:
– радиус описанной около треугольника
окружности. Отсюда получаем:


Значит,
 .
.
Высоту
 найдем из прямоугольного треугольника
найдем из прямоугольного треугольника :
:
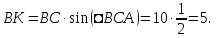
Ответ:
 .
.
