2.5 Площадь круга

Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.

Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π. [3, c. 98]

Это интересно:

Число π представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение получило применение после работ Л. Эйлера в 1737 г. [8,c. 177]

Площадь окружности можно вычислить через константу π и радиус окружности. Формула площади круга через радиус выглядит так:

Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности:

Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.

Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:

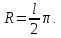
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности:

Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.

Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности.

Зная сторону, a ее можно найти по теореме Пифагора:, отсюда.

После того, как найдем диагональ – мы сможем рассчитать радиус: .

Рисунок 2.5.1

И после подставим все в основную формулу площади круга описанного вокруг квадрата:.

Пример 2.5.1.

Найдите площадь круга, если длина окружности .

Решение: , откуда имеем Тогда

Ответ:

Пример 2.5.2.

В круге радиуса проведены по разные стороны от центра две параллельные хорды, одна из которых стягивает дугу в, другая – Найти площадь части круга, заключённого между хордами. [7,c. 78]

Решение:

Рисунок 2.5.2

Площадь сегмента с дугой равна, а площадь сегмента с дугойравна. Искомая площадь составляет

Ответ:

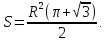
Пример 2.5.3.

Две окружности радиуса пересекаются так, что каждая проходит через центр другой. Две другие окружности того же радиуса имеют центры в точках пересечения первых двух окружностей. Найти площадь, общую всем четырём кругам.

Решение:

Каждая из двух последних окружностей проходит через центры первых двух (рисунок 2.5.3), поэтому длина общей хорды .

Рисунок 2.5.3

Искомая площадь равна удвоенной площади сегмента с центральным углом , то есть

Ответ:

2.6 Площадь произвольного n-угольника

Отдельно в школе площадь произвольного многоугольника не рассматривается. Однако, в курсе геометрии есть ряд задач, в которых требуется найти площадь произвольного многоугольника. К тому же на практике задача о площади такого многоугольника встречается довольно часто. Поэтому на уроках геометрии следует уделить должное внимание решению подобных задач. Методическая ценность такого рода задач заключается в том, что они, во-первых, хорошо иллюстрируют свойство аддитивности площади, а, во-вторых, помогают учащимся развить навыки нахождения площади треугольника различными способами.

Итак, основная идея нахождения площади произвольного n-угольника – это разбиение его на конечное число треугольников. В результате суммирования площадей треугольников, составляющих данный n-угольник получается искомая площадь.

Нахождение площади n-угольника таким способом лежит в основе доказательства теоремы о площади трапеции. [9, c. 21]

Теорема. Площадь трапеции равна произведению полусуммы ее оснований на высоту. [10, c. 70]

Доказательство. Рассмотрим трапецию с основаниямии, высотойи площадью.

Рисунок 2.6.1

Докажем, что .

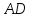Диагональ разделяет трапецию на два треугольникаи, поэтому. Примем отрезкииза основание и высоту треугольника, а отрезки BC и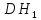за основание и высоту треугольника. Тогда,. Так как, то. Таким образом,.

Теорема доказана.

Пример 2.6.1.

Основание треугольника равно 30 см, а боковые стороны 26 и 28 см. Высота разделена в отношении (считая от вершины), и через точку деления проведена прямая, параллельная основанию. Определить площадь полученной при этом трапеции.

Решение:

По условию, (рисунок 2.6.2).

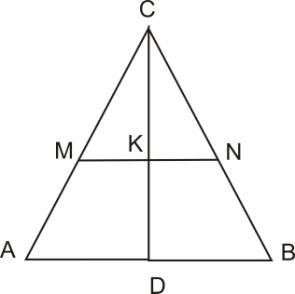
Рисунок 2.6.2

Тогда и по формуле Герона находимТак как , то Отсюда определяем площадь трапеции:

Ответ:

Пример 2.6.2.

Диагональ равнобедренной трапеции делит её тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции.

Решение:

По условию, (рисунок 2.6.3). Но , а значит,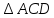– равнобедренный и . Имеемтак как, то. Проведём; тогдаи изнаходимИтак,

Рисунок 2.6.3

Ответ:).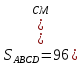

Пример 2.6.3.

Найти площадь равнобедренной трапеции, если её высота равна , а боковая сторона видна из центра описанной окружности под углом.

Решение:

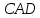Так как центральный угол равен (рисунок 2.6.4), то вписанный угол равен.

Рисунок 2.6.4

Следовательно, и из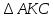получаем:

. Находим площадь трапеции:

Ответ:

Пример 2.6.4.

В некоторый угол вписана окружность радиуса , а длина хорды, соединяющей точки касания, равна. Параллельно этой хорде проведены две касательные, в результате чего получилась трапеция. Найти площадь этой трапеции.

Решение:

Пусть 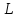и– точки касания (рисунок 2.6.5); тогдаоткудапоскольку Проведём 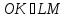и. Тогда искомая площадь. Для описанной трапеции имеемпоэтому.

Далее, 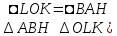как углы с взаимно перпендикулярными сторонами, откуда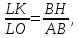илии, значит,

.

Рисунок 2.6.5

Итак, .

Ответ: