1 Роль и место понятия «площадь в школьном» курсе математики

Словом площадь школьники пользуются уже в начальной школе. Математика в начальных классах – это, прежде всего, знакомство с основными математическими терминами, понятиями и величинами, одной из которых и является площадь. Однако, непосредственное введение понятия «площадь» и изучение площади как величины начинается только в пятом классе. Геометрический материал в I-VI классах распределен по всему курсу математики. Он составляет содержание так называемого пропедевтического курса геометрии. Основные цели этого курса – подготовить учащихся к сознательному усвоению систематического курса геометрии VII-IX классов. Задачами данного курса являются развитие у учащихся логического мышления, знакомство их с основными геометрическими понятиями, развитие пространственного мышления; формирование навыков измерения геометрических величин, построения геометрических фигур и т.д. Но и перейдя в пятый класс, учащиеся не сразу приступают к изучению площади. Это понятие вводится только во второй четверти. Как и в случае введения любого другого понятия, введению понятия «площадь» должно предшествовать изучение ряда объектов и понятий, на которые учащиеся опираются при изучении данного понятия. В нашем случае такими понятиями являются отрезок, длина отрезка, квадрат числа.[1, c. 144]

В школьных учебниках площадь многоугольника определяется с помощью указания ее свойств:

численное значение площади любого многоугольника всегда положительно;

площади равных многоугольников, т.е. многоугольников, которые можно совместить с помощью движения, одинаковы;

площадь многоугольника, полученного объединением двух многоугольников, не имеющих общих внутренних точек, равна сумме площадей составляющих многоугольников (многоугольники, не имеющие общих внутренних точек, будем называть не перекрывающимися);

площадь квадрата со стороной единичной длины равна единице. В различных учебниках определения площади несколько отличаются друг от друга, но суть определений совпадает с указанным выше.

Таким образом, площадь многоугольников мож­но трактовать как функцию , заданную на множестве всех многоугольников, принимаю­щую числовые значения и обладающую следующи­ми свойствами (их иногда называютаксиомами площади):

(положительность площади) для любого мно­гоугольника справедливо;

(инвариантность площади) если , то символ «» здесь обозначает, что многоугольники и могут быть совмещены движением;

(аддитивность площади) если и многоугольники и 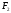не перекрываются, то ;

(нормированность площади) для квадрата со стороной единичной длины .

Это определение по своему характеру сродни, например, определению арифметического корня : b – есть неотрицательное число, n-я степень которого равна .

Ведь и в этом случае арифметический корень определяется указанием его свойств. Для корректного определения арифметического корня надо доказать, что такое число, во-первых, существует и, во-вторых, единственно. Первое следует из того, что множество значений функциии есть. Второе следует из строго монотонного возрастания рассматриваемой функции.

Для корректного определения площади многоугольников функции требуется доказать, что такая функция существует и единственна.

Многим сам вопрос (об определении площади) покажется искусственным: они скажут, что площадь – первичное понятие, не подлежащее определению.

Взгляд на площадь как на первичное понятие сложился еще в древности. До недавнего времени этого взгляда придерживались и математики. На протяжении многих столетий они видели задачу в вычислении площадей; им не приходило в голову, что «площадь» нуждается в специальном определении.

Между тем их вычисления должны были на чем-то основываться – если не на прямом определении, то на чем-то, его заменяющем, на каких-то принципах, которые позволяли им всякий раз получать в качестве площади определенное число. И такие принципы, конечно, существовали, хотя обычно не формулировались. Это основные свойства площади. Так, в школьных учебниках площадь многоугольников вообще не определяется, но указываются ее свойства, соответствующие аксиомам площади, или определения носят формально-дескриптивный характер, но свойства, определяющие площадь, используются не для построения общей функции , а для вычисления площади основных плоских фигур: прямоугольника, параллелограмма, треугольника, трапеции и плоских фигур, составленных из этих основных.

Познакомившись с понятием «площадь» в пятом классе и научившись измерять площадь плоских фигур непосредственно (путем подсчета единичных квадратов, умещающихся в данной фигуре), учащиеся сталкиваются с проблемой неточности при таком способе измерения. Здесь вводится так называемый косвенный метод измерения площади. То есть площадь не измеряется, а вычисляется по какой-то формуле. И поэтому на протяжении всего курса математики школьники учатся не измерять, а вычислять площади плоских геометрических фигур с помощью формул.