
- •Линейная и векторная алгебра
- •Общие методические указания
- •Операции над матрицами.
- •Определители матриц второго и третьего порядка.
- •Системы линейных алгебраических уравнений
- •Построение общего решения методом Гаусса:
- •Задание 1
- •Задание 2
- •Задание 3.
- •Векторная алгебра и аналитическая геометрия.
- •4 Прямая на плоскости
- •Плоскость.
- •Прямая и плоскость в пространстве.
- •Задание 4.
- •Задание 7.
- •Задание 8
- •Кривые второго порядка
- •Окружность
- •Гипербола
- •Парабола
Задание 4.
Коллинеарны ли
векторы
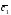 и
и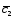 ,
построенные по векторам
,
построенные по векторам
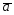 и
и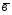 ?
?
1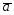 .={1;-2;3};
.={1;-2;3};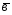 ={3;0;-1};
={3;0;-1};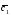 =2
=2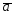 +4
+4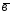 ;
;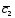 =3
=3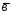 -
-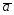 ;
;
2.
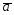 ={1;0;1};
={1;0;1};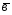 ={-2;3;5};
={-2;3;5};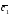 =
=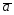 +2
+2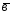 ;
;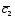 =3
=3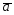 -
-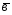 ;
;
3.
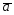 ={-2;4;1};
={-2;4;1};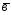 ={1;-2;7};
={1;-2;7};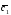 =5
=5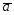 +3
+3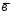 ;
;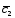 =2
=2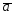 -
-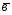 ;
;
4.
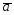 ={1;2;-3};
={1;2;-3};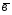 ={2;-1;-1};
={2;-1;-1};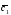 =4
=4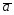 +3
+3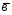 ;
;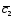 =8
=8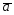 -
-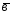 ;
;
5.
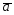 ={3;5;4};
={3;5;4};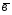 ={5;9;7};
={5;9;7};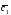 =-2
=-2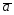 +
+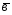 ;
;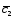 =3
=3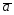 -
-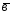 ;
;
6.
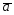 ={1;4;-2};
={1;4;-2};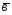 ={1;1;-1};
={1;1;-1};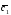 =
=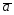 +
+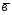 ;
;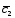 =4
=4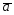 +2
+2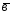 ;
;
7.
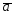 ={1;-2;5};
={1;-2;5};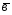 ={3;-1;0};
={3;-1;0};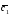 =4
=4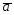 -2
-2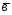 ;
;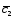 =
=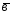 -2
-2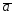 ;
;
8.
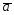 ={3;4;-1};
={3;4;-1};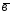 ={2;-1;1};
={2;-1;1};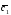 =6
=6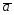 -3
-3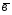 ;
;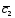 =
=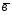 -2
-2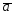 ;
;
9.
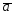 ={-2;-3;-2};
={-2;-3;-2};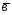 ={1;0;5};
={1;0;5};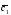 =3
=3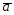 +9
+9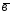 ;
;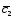 =-3
=-3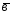 -
-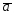 ;
;
10.
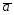 ={-1;4;2};
={-1;4;2};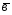 ={3;-2;6};
={3;-2;6};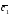 =2
=2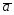 -
-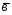
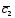 =3
=3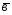 -6
-6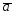 ;
;
11.
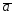 ={1;-2;3};
={1;-2;3};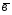 ={3;0;-1};
={3;0;-1};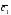 =2
=2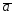 +4
+4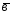 ;
;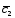 =3
=3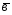 -
-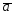 ;
;
12.
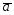 ={0;3;-2};
={0;3;-2};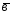 ={1;-2;1};
={1;-2;1};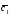 =5
=5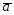 -2
-2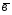 ;
;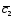 =3
=3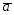 +5
+5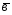 ;
;
13.
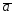 ={-2;7;-1};
={-2;7;-1};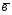 ={-3;5;2};
={-3;5;2};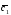 =2
=2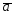 +3
+3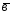 ;
;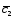 =3
=3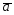 +2
+2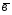 ;
;
14.
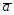 ={3;7;0};
={3;7;0};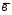 ={1;-3;4};
={1;-3;4};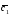 =4
=4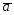 -2
-2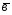 ;
;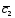 =
=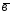 -2
-2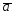 ;
;
15.
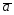 ={-1;2;-1};
={-1;2;-1};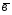 ={2;-7;1};
={2;-7;1};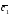 =6
=6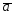 -2
-2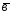 ;
;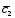 =4
=4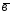 -
-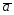 ;
;
16.
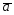 ={7;9;-2};
={7;9;-2};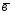 ={5;4;3};
={5;4;3};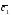 =4
=4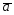 -
-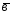 ;
;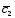 =4
=4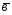 -
-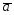 ;
;
17.
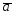 ={5;0;-2};
={5;0;-2};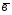 ={6;4;3};
={6;4;3};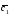 =5
=5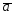 -3
-3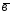 ;
;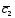 =6
=6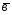 -10
-10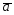 ;
;
18.
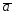 ={8;3;-1};
={8;3;-1};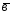 ={4;1;3};
={4;1;3};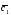 =2
=2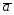 -
-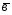 ;
с2=2
;
с2=2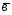 -4
-4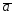 ;
;
19.
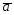 ={3;-1;6};
={3;-1;6};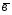 ={5;7;10};
={5;7;10};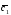 =4
=4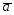 -2
-2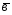 ;
с2=
;
с2=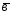 -2
-2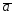 ;
;
20.
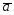 ={1;-2;4};
={1;-2;4};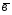 ={7;3;5};
={7;3;5};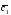 =6
=6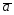 -3
-3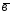 ;
;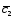 =
=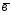 -2
-2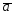 ;
;
21.
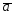 ={3;7;0};
={3;7;0};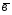 ={4;6;-1};
={4;6;-1};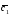 =3
=3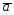 +2;
+2;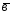
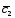 =5
=5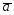 -7
-7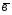 ;
;
22.
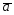 ={2;-1;4};
={2;-1;4};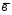 ={3;-7;-6};
={3;-7;-6};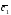 =2
=2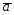 -3
-3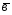 ;
;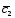 =3
=3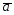 -2
-2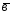 ;
;
23.
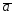 ={5;-1;-2};
={5;-1;-2};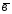 ={6;0;7};
={6;0;7};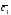 =3
=3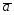 -2
-2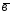 ;
;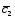 =4
=4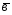 -6
-6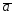 ;
;
24.
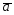 ={3;7;0};
={3;7;0};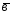 ={1;-3;4};
={1;-3;4};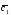 =4
=4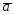 -2
-2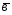 ;
;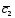 =
=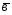 -2
-2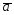 ;
;
25.
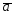 ={1;-2;5};
={1;-2;5};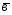 ={3;-1;0};
={3;-1;0};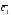 =4
=4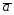 -2
-2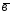 ;
;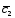 =
=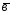 -2
-2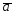 ;
;
26.
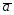 ={5;-1;-2};
={5;-1;-2};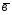 ={6;0;7};
={6;0;7};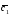 =3
=3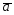 -2
-2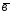 ;
;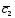 =4
=4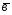 -6
-6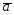 ;
;
27.
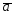 ={1;-2;4};
={1;-2;4};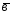 ={7;3;5};
={7;3;5};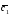 =6
=6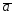 -3
-3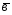 ;
;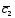 =
=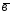 -2
-2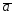 ;
;
28.
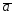 ={3;5;4};
={3;5;4};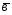 ={5;9;7};
={5;9;7};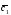 =-2
=-2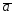 +
+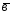 ;
;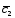 =3
=3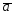 -2
-2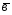 ;
;
29.
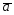 ={-1;2;-1};
={-1;2;-1};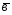 ={2;-7;1};
={2;-7;1};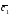 =6
=6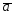 -2
-2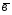 ;
;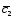 =
=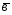 -3
-3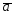 ;
;
30.
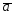 ={1;-2;3};
в ={3;0;-1};
={1;-2;3};
в ={3;0;-1};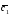 =2
=2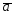 +4
+4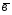 ;
;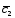 =3
=3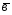 -
-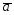 ;
;
31.
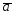 ={2;-3;2};
={2;-3;2};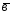 ={7;1;-2};
={7;1;-2};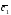 =3
=3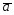 -4
-4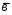 ;
;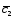 =2
=2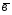 -
-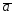 ;
;
32.
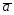 ={2;1;-1};
={2;1;-1};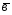 ={3;4;0};
={3;4;0};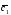 =3
=3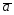 -4
-4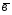 ;
;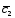 =2
=2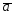 +
+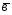 ;
;
33.
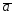 ={2;0;2};
={2;0;2};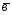 ={1;-1;4};
={1;-1;4};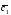 =
=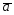 -2
-2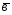 ;
;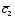 =2
=2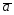 +3
+3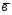 ;
;
34.
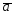 ={1;2;-2};
={1;2;-2};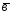 ={5;2;3};
={5;2;3};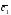 =3
=3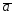 +
+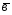 ;
;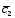 =3
=3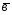 -;
-;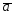
Задание 5.
Найти косинус угла
между векторами
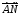 и
и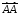
1.А(1;-2;3); В(0;-1;2); С(3;-4;5)
2.А(0;-3;6); В(-12;-3;-3); С(-9;-3;-6)
3. А(3;3;-1); В(5;5;-2); С(4;1;1)
4. А(-1;2;-3); В(3;4;-6); С(1;1;-1)
5. А(-4;-2;0); В(-1;-2;4); С(3;-2;1)
6. А(5;3;-1); В(5;2;0); С(6;4;-1)
7. А(-3;-7;-5); В(0;-1;-2); С(2;3;0)
8. А(2;-4;6); В(0;-2;4); С(6;-8;10)
9. А(0;1;-2); В(3;1;2); С(4;1;1)
10. А(3;3;-1); В(1;5;-2); С(4;1;1)
11. А(2;1;-1); В(6;-1;-4); С(4;2;1)
12. А(-1;-2;1); В(-4;-2;5); С(-8;-2;2)
13. А(6;2;-3); В(6;3;-2); С(7;3;-3)
14. А(0;0;4); В(-3;-6;1); С(-5;-10;-1)
15. А(2;-8;-1); В(-3;-6;0); С(-2;-5;-1)
16. А(3;-6;9); В(0;-3;6); С(9;-12;15)
17. А(0;2;-4); В(8;2;2); С(6;2;4)
18. А(3;3;-1); В(5;1;-2); С(4;1;1)
19. А(-4;3;0); В(0;1;3); С(-2;4;-2)
20. А(1;-1;0); В(-2;-1;4); С(8;-1;-1)
21. А(7;0;2); В(7;1;3); С(8;-1;2)
22. А(2;3;2); В(-1;-3;-1); С(-3;-7;-3)
23. А(2;2;7); В(0;0;6); С(-2;5;7)
24. А(0;2;-4); В(8;2;2); С(6;2;4)
25. А(3;3;-1); В(5;1;-2); С(4;1;1)
26. А(-4;3;0); В(0;1;3); С(-2;4;-2)
27. А(1;-1;0); В(7;1;3); С(8;-1;-1) .
28. А(7;0;2); В(-2;-1;4); С(8;-1;2)
29. А(2;3;2); В(-1;-3;-1); С(-3;-7;-3)
30. А(2;2;7); В(0;0;6); С(-2;5;7)
31. А(2;1;-2); В(3;4;2); С(1;-2;0)
32. А(1;-1;2); В(4;3;-2); С(2;1;-1)
33. А(4;5;-3); В(2;1;5); С(4;2;-1)
34. А(1;2;-2); В(4;-3;-4); С(3;5;0)
Задание 6.
Вычислить объём тетраэдра с вершинами в точках А1, А2, А3, А4 и его высоту, опущенную из вершины А4 на грань А1А2А3.
1. А1(1;3;6); А2(2;2;1); А3(-1;0;1); А4(-4;6;-3)
2. А1(-4;2;6); А2(2;-3;0); А3(-10;5;8); А4(-5;2;-4)
3. А1(7;2;4); А2(7;-1;-2); А3(3;3;1); А4(-4;2;1)
4. А1(2;1;4); А2(-1;5;-2); А3(-7;-3;2); А4(-6;-3;6)
5. А1(-1;-5;2); А2(-6;0;-3); А3(3;6;-3); А4(-10;6;7)
6. А1(0;-1;-1); А2(-2;3;5); А3(1;-5;-9); А4(-1;-6;3)
7. А1(5;2;0); А2(2;5;0); А3(1;2;4); А4(-1;1;1)
8. А1(2;-1;-2); А2(1;2;1); А3(5;0;-6); А4(-10;9;-7)
9. А1(-2;0;-4); А2(-1;7;1); А3(4;-8;-4); А4(1;-4;6)
10. А1(14;4;5); А2(-5;-3;2); А3(-2;-6;-3); А4(-2;2;-1)
11. А1(1;2;0); А2(3;0;-3); А3(5;2;6); А4(8;4;-9)
12. А1(2;-1;2); А2(1;2;-1); А3(3;2;1); А4(-4;2;5)
13. А1(1;3;6); А2(2;2;1); А3(-1;0;1); А4(-4;6;-3)
14. А1(2;3;1); А2(4;1;-2); А3(6;3;7); А4(7;5;-3)
15. А1(1;1;-1); А2(2;3;1); А3(3;2;1); А4(5;9;-8)
16. А1(1;5;-7); А2(-3;6;3); А3(-2;7;3); А4(-4;8;-12)
17. А1(-3;4;-7); А2(1;5;-4); А3(-5;-2;0); А4(2;5;4)
18. А1(-1;2;-3); А2(4;-1;0); А3(2;1;-2); А4(3;4;5)
19. А1(4;-1;3); А2(-2;1;0); А3(0;-5;1); А4(3;2;-6)
20. А1(1;-1;1); А2(-2;0;3); А3(2;1;-1); А4(2;-2;-4)
21. А1(1;2;0); А2(1;-1;2); А3(0;1;-1); А4(-3;0;1)
22. А1(1;0;2); А2(1;2;-1); А3(2;-2;1); А4(2;1;0)
23. А1(1;2;-3); А2(1;0;1); А3(-2;-1;6); А4(0;-5;-4)
24. А1(1;1;-1); А2(5;9;-8); А3(2;3;1); А4(3;2;1)
25. А1(-1;1;1); А2(5;2;0); А3(2;5;0); А4(1;2;4)
26. А1(2;-2;-4); А2(1;-1;1); А3(2;1;-1); А4(-2;0;3)
27. А1(2;1;4); А2(-7;-3;2); А3(-1;5;-2); А4(-6;-3;6)
28. А1(2;2;1); А2(1;3;6); А3(-4;6;-3); А4(-1;0;1)
29. А1(8;4;-9); А2(5;2;6); А3(3;0;-3); А4(1;2;0)
30. А1(0;-5;-4); А2(-2;1;6); А3(1;2;-3); А4(1;0;1)
31. А1(-2;2;3); А2(4;0;7); А3(2;-3;1); А4(-4;6;-3)
32. А1(2;-1;-3); А2(-4;3;3); А3(2;0;7); А4(4;-5;-2)
33. А1(-6;0;-3); А2(3;6;-3); А3(2;7;-5); А4(1;-1;0)
34. А1(2;3;1); А2(1;1;-1); А3(4;2;5); А4(7;3;-2)
