Министерство сельского хозяйства Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Саратовский государственный аграрный университет

имени Н. И. Вавилова»

Линейная и векторная алгебра

Методические указания и задания

для выполнения типового расчета

по курсу «Математика»

Направление подготовки

260100.62 Продукты питания из растительного сырья

Саратов 2013

Линейная и векторная алгебра: метод. указания и задания для выполнения типового расчета по курсу «Математика» для направления подготовки 260100.62 Продукты питания из растительного сырья, 221400.62 Управление качеством / сост. Н.В. Дьяконова //ФГБОУ ВПО «Саратовский ГАУ».- Саратов, 2013.-

Методические указания и задания для выполнения типового расчета по дисциплине «Математика» составлены в соответствии с программой и предназначены для студентов направления подготовки 260100.62 Продукты питания из растительного сырья, 221400.62 Управление качеством. Они содержат рекомендации, примеры и задания к выполнению типового расчета. Позволяют студентам освоить основные математические методы, необходимые для анализа процессов и явлений в ходе поиска оптимальных решений практических задач, обучает методам обработки и анализа результатов эксперимента. Курс нацелен на формирование ключевых компетенций, необходимых для эффективного решения профессиональных задач и организации профессиональной деятельности.

1. Общие методические указания

1. Работа выполняется на листах формата А4 (210х297), которые затем скрепляются.

2. Решение заданий следует сопровождать краткими пояснениями.

3. Исходные данные для заданий типового расчета представлены в таблицах. Из таблицы каждый студент выбирает строки с номерами вариант, которые соответствуют номеру в списке группового журнала.

2. Матрицы и определители.

Определение 1.1. Прямоугольная таблица чисел вида

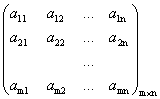
называется прямоугольной матрицей размера 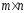, где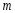- количество строк, а- количество столбцов.

Определение 1.2. Квадратной матрицей 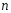-го порядка называется матрица размера .

Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали равны нулю. Единичной матрицей (Е) называется диагональная матрица с единицами на главной диагонали.

Операции над матрицами.

Суммой матриц A=(a_ij) и B=(b_ij) одинакового размера называется матрица C=(c_ij) того же размера, причем c_ij=a_ij+b_ij,

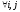
Для любых матриц A,B,C одного размера выполняются равенства:

1. A+B=B+A (коммутативность);

2. (A+B)+C=A+(B+C)=A+B+C (ассоциативность)

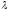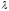Произведением матрицы A=(a_ij) на число называется матрицаB=(b_ij) того же размера, что и матрица А, причем b_ij=a_ij ,

Пример №1. Выполнить действия:

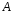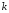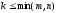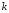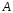Определение 1.3. Выберем в матрице размерапроизвольныестрок истолбцов,. Элементы, стоящие на пересечении выбранных строк и столбцов образуют квадратную матрицу-го порядка, определитель которой называют минором-го порядка матрицы. Элементы матрицы являются минорами первого порядка.

Если в матрице 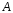имеется минор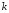-го порядка, не равный нулю, а все ее миноры-го порядка, окаймляющие этот минор, равны нулю, то ранг матрицы равен.

Определение 1.4. Матрица называется обратной для квадратной матрицы, если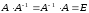

Квадратная матрица имеет обратную тогда и только тогда, когда ее определитель не равен нулю. Квадратная матрица 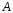, определитель которой отличен от нуля имеет единственную обратную матрицу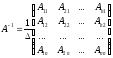, где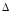- определитель матрицы;

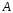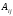- алгебраическое дополнение элемента матрицы.

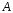Элементарными преобразованиями строк (столбцов) матрицы называются следующие преобразования:

а) умножение й строки матрицы на число;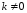

б) прибавление к 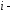й строке (столбцу)й строки (столбца), умноженной на число;

в) перестановка 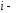й и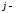й строк (столбцов) матрицы.

Алгоритм построения обратной матрицы с помощью элементарных преобразований строк матрицы:

1. К данной матрице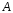приписать справа единичную матрицу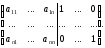

2. С помощью элементарных преобразований объединенной матрицы привести матрицу 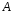к единичной матрице

3. Матрица 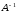имеет вид: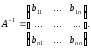

Обратная матрица позволяет найти решения следующих матричных уравнений: 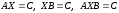. Решением этих уравнений являются соответственно матрицы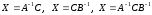. В этих уравнениях– матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров.

Пример №2. Вычислить:

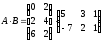
Решение:

При вычислении произведения матриц, всегда надо помнить, что произведение существует, только если число столбцов матрицы А равно числу строк матрицы В. В нашем случае матрица А имеет размерность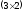, матрица В -; число столбцов матрицы А равно 2, число строк матрицы В равно 2. Размерность матрицы произведения будет.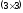

Пример №3. Выполнить действия:

Решение:

Пример №4. Вычислить ранг матрицы

Решение:

Найдём ранг матрицы методом элементарных преобразований. Метод элементарных преобразований нахождения ранга матрицы заключается в том, что матрицу приводят к ступенчатому виду с помощью элементарных преобразований, количество нулевых строк полученной ступенчатой матрицы - искомый ранг матрицы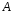. Приведём матрицу к ступенчатому виду:

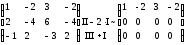
Полученная ступенчатая матрица содержит одну не нулевую строку, значит её ранг равен единице.

Пример №5. Найти обратную матрицу к матрице

Решение:

Найдем обратную матрицу к данной, методом присоединенной матрицы.

1) Найдем 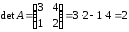не равен 0.

Матрица 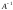существует, если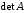не равен 0.

2) Найдем алгебраические дополнения к элементам матрицы :

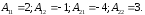
3) Запишем присоединённую матрицу:

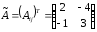
4) Найдём обратную матрицу

Сделаем проверку:

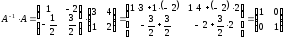
В результате произведения 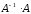получили единичную матрицу, следовательно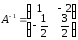

Обратная матрица к матрице .

Пример №6. Решить матричное уравнение:

Решение:

1)Найдем detA:

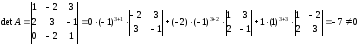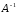Так как detA0, то матрица существует.

2) Найдем алгебраические дополнения ко всем элементам матрицы :

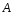3) Запишем матрицу

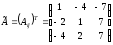
4)Найдем матрицу :

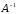Проверка:

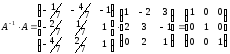
Следовательно:

Проверка:

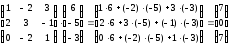
Задания:

1. Найти сумму матриц ,

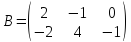
2. Даны матрицы 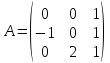и 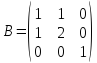. Найти матрицу.

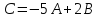3. Найти произведение матриц, если оно существует:

а) ;

б)

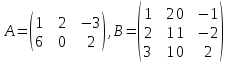
в)

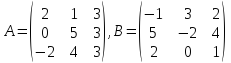
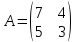4. Для матрицы найти обратную методом присоединенной матрицы.

5. Найти матрицу, обратную к матрице

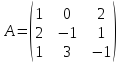
6. Найти ранг матрицы