Контрольные вопросы

1. Какие условия должны выполняться при электрическом моделировании температурного поля наружного угла?

2. Как моделируются граничные условия на поверхностях угла? В чем скажется, если здесь допущено какое-либо отклонение?

3. Какие негативные явления наблюдаются в углах ограждений? Почему?

4. При какой наружной температуре t_н температура угла t_у будет равна температуре внутренней поверхности вдали от угла – t_в.п? Проанализируйте формулы (2.2) и (2.3).

5. Какие меры необходимо принять для исключения негативных явлений (выделение влаги), наблюдаемых в углах ограждений?

Литература

1. СНиП РФ 23-02-2003 «Тепловая защита зданий»; СП 23-101-2004 «Проектирование тепловой защиты зданий».

2. Федорчук Н.М., Грызлов В.С. Избранные главы физики в строительном деле. Учеб. пособие. – Череповец, 1994.

3. Шильд Е.Х., Кассельман Ф., Дамен Г., Поленц Р. Строительная физика. – М: Стройиздат, 1982.

Работа 3

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ТЕПЛОПРОВОДНОГО ВКЛЮЧЕНИЯ НА ТЕМПЕРАТУРНОЕ ПОЛЕ СТЕНЫ (ЭЛЕКТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ)

Цель работы − исследование температурного поля наружной стены с теплопроводным включением; расчеты термических сопротивлений; тепловых потоков.

Оборудование: установка − электрическая модель фрагмента наружной стены с теплопроводным включением.

3.1. Теоретическое введение [1]

Указания: перед выполнением данной работы необходимо изучить теоретическое введение к работе 1 «Исследование температурного поля наружной стены методом электрического моделирования».

В реальных ограждающих конструкциях с целью увеличения их устойчивости широко используют введение в материал ограждений различных металлических каркасов, балок. Обычно каркасы и балки изготавливаются из материалов, теплопроводность которых значительно выше по сравнению с обычными материалами (кирпич, легкие бетоны и проч.). В результате введения теплопроводных включений тепловое поле ограждающей конструкции становится неоднородным. Общее тепловое сопротивление ограждения уменьшается. Кроме того, при недостаточном тепловом сопротивлении на внутренней поверхности конструкций в местах теплопроводных включений вероятно выпадение конденсата, что является недопустимым.

Существуют приближенные методы расчета низшей температуры в местах теплопроводных включений, которые разработаны лишь для ограниченных форм конструкций. Для теплопроводного включения, которое исследуется в данной работе, таких методов пока не существует. Поэтому низшую температуру определяют экспериментально с помощью электрической модели.

Для определения приведенного термического сопротивления неоднородной конструкции, изображенной на рис. 3.1, К.Ф. Фокиным был разработан аналитический метод расчета − метод разбиений, суть которого заключается в следующем.

• Плоскостями, параллельными направлению теплового потока, ограждающая

конструкция условно делится на участки, которые относительно друг друга являются параллельными (рис. 3.2). В данном случае это участки 1, 2 и 3 (рис. 3.2 и 3.3, а). Сопротивление всего фрагмента конструкции определяется в этом случае по формуле:

(3.1)

где F₁, F₂, F₃ − площади участков 1, 2 и 3 соответственно; R₁, R₂, R₃ − термические сопротивления участков 1, 2 и 3.

Рис. 3.1. Модель фрагмента неоднородной конструкции

Из рисунка 3.1 видно, что

F₀ = F₁ + F₂ + F₃ = H (l₁ + l₂ + l₃),

где H − высота конструкции (задавать её не обязательно).

Рис. 3.2. Схема разбиения фрагмента неоднородной конструкции

Термическое сопротивление однородного участка (слоя) определяется по формуле:

, где (не Омы).

Плоскостями, перпендикулярными к направлению потока тепла, ограждающая конструкция условно разрезается на участки, которые относительно друг друга являются соединенными последовательно. В данном случае это участки I, II и III (смотри рис. 3.2 и 3.3,б). Сопротивление всего фрагмента конструкции тогда определяется по формуле:

(3.2)

а) б)

Рис.3.3. Сопротивления и коэффициенты теплопроводности участков после разбиения конструкции.

Опыт показывает, что величина , рассчитанная по формуле (3.1), всегда меньше истинного значения сопротивления конструкции, а величина , вычисленная по формуле (3.2), соответственно больше этого значения. Поэтому так называемое приведенное термическое сопротивление конструкции рекомендуется определять по формуле:

(3.3)

При этом предполагается, что в формуле (3.1)

, на модели δ₁ = δ₃.

В работе с моделью (3.5),

где k – коэффициент геометрического подобия «Модель – конструкция»; δ₁, δ₂, δ₁ – толщины участков I, II и III на модели соответственно λ₁, λ₂ – коэффициенты теплопроводности материалов стены и включения соответственно; l₁ = l₃, l₂ − площади, на модели фрагмента стены соответственно

В формуле (3.2):

; , на модели F₁ = F₃.

В работе с моделью 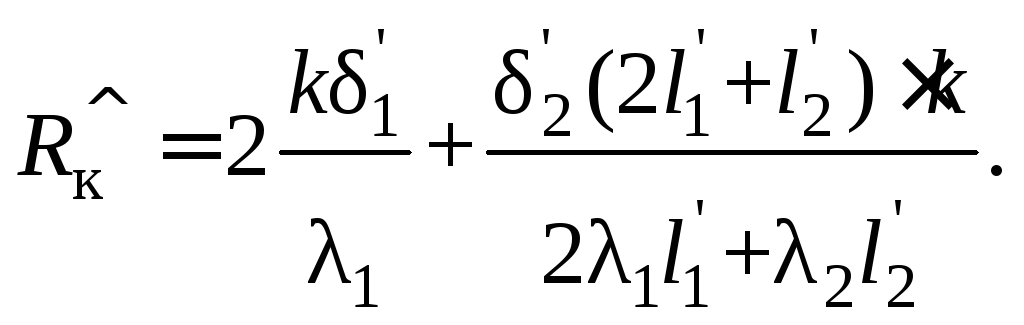(3.5) .

Общее значение термического сопротивления ограждающей конструкции определяется по формуле:

,

где пристеночные сопротивления , (работа 1).