Умови задач с.4.0.А - с.4.9.А (оцінка чотири бали)

Номер умови	Сила Н
	Точка прикладання
0	K	60	30	45
1	L	30	15	65
2	M	45	75	60
3	L	30	55	75
4	K	60	30	10
5	K	65	40	25
6	H	30	10	45
7	L	15	35	60
8	K	25	60	35
9	L	55	30	75

Таблиця 12

Умови задач с.4.0.Б - с.4.9.Б (оцінка п’ять балів)

Номер умови	Сила Н
	Точка прикладання
0	M	20	75	30
1	H	10	30	55
2	H	15	65	25
3	M	20	55	30
4	H	35	40	75
5	M	15	45	60
6	M	30	50	70
7	H	65	25	40
8	H	15	35	55
9	M	50	25	10

2. Тепер розглянемо рівновагу вузла Н.

На вузол діють задана сила і реакції стержнів (див. рис. 26.15). При цьому за законом про рівність дії та протидії реакція має напрямок, протилежний до , а за величиною . Слід зазначити, що при визначенні проекції сили на осі x i y зручніше спочатку знайти проекцію цієї сили на площину xy (за величиною ), а потім цю проекцію на площину проектувати на осі. Складемо рівняння рівноваги:

(4)

(5)

(6)

З рівняння (5) визначимо:

Н.

З рівняння (4) знайдемо:

Н.

З рівняння (6) визначимо:

Н.

Відповідь: Н; Н; Н; Н; Н; Н.

Знаки показують, що стержні 2, 4 і 5 стиснуті, а інші стержні – розтягнуті.

Приклад розв’язання задачі С.4. Другий рівень складності

Шість невагомих стержнів з’єднані своїми кінцями шарнірно один з одним у двох вузлах і прикріплені іншими кінцями, також шарнірно, до нерухомих опор А, В, С, D (рис. 26.16). Вузли розташовані у вершинах К і Н прямокутного паралелепіпеда. У першому вузлі прикладені сили і , а в другому вузлі - сила . Сила утворює з додатними напрямками координатних осей x, y, z кути , сила - кути , а сила - кути . Грані паралелепіпеда, паралельні до площини xy – квадрати. Діагоналі інших (бічних) граней утворюють з площиною xy кут , а діагональ паралелепіпеда утворює з цією площиною кут .

Дано: Н; Н; Н;

Визначити: зусилля в стержнях 1 - 6.

Розв’язання. 1. Розглянемо рівновагу вузла К, у якому сходяться стержні 1, 2, 3 (див. рис. 26.16). На вузол діють задані сили і та реакції стержнів, які покажемо вздовж стержнів від вузла, вважаючи стержні розтягнутими. Складемо рівняння рівноваги цієї просторової системи збіжних сил:

(1)

(2)

(3)

З рівняння (3) визначимо:

Н.

З рівняння (1) одержимо:

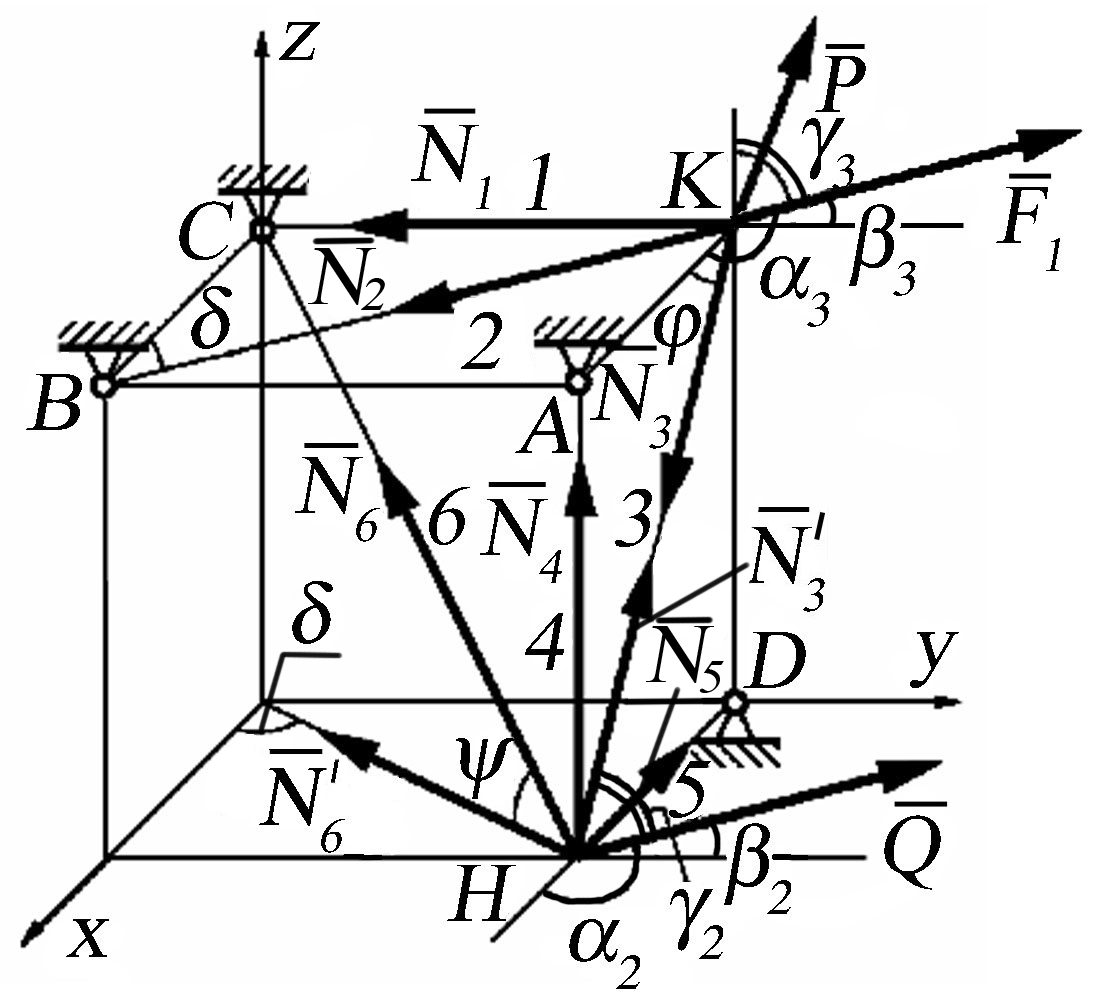
Рис. 26.16

Н.

З рівняння (2) знайдемо:

Н.

2. Тепер розглянемо рівновагу вузла Н.

На вузол діють задана сила і реакції стержнів (див. рис. 26.16). При цьому за законом про рівність дії та протидії реакція має напрямок, протилежний до , а за величиною . Слід зазначити, що при визначенні проекції сили на осі x i y зручніше спочатку знайти проекцію цієї сили на площину xy (за величиною ), а потім цю проекцію на площину проектувати на осі. Складемо рівняння рівноваги:

(4)

(5)

(6)

З рівняння (5) визначимо:

Н.

З рівняння (4) знайдемо:

Н.

З рівняння (6) одержимо:

Н.

Відповідь:Н;Н;Н;Н;Н;Н.

Знаки показують, що стержні 2, 4, 5 стиснуті, а інші стержні – розтягнуті.

Приклад розв’язання задачі С.4. Третій рівень складності

Шість невагомих стержнів з’єднані своїми кінцями шарнірно один з одним у двох вузлах і прикріплені іншими кінцями, також шарнірно, до нерухомих опор А, В, С, D (рис. 26.17). Вузли розташовані у вершинах К і Н прямокутного паралелепіпеда. У першому вузлі прикладені сили і , а в другому вузлі - сили і . Сила утворює з додатними напрямками координатних осей x, y, z кути , сила - кути , сила - кути , а сила - кути . Грані паралелепіпеда, паралельні до площини xy – квадрати. Діагоналі інших (бічних) граней утворюють з площиною xy кут , а діагональ паралелепіпеда утворює з цією площиною кут .

Дано: Н; Н; Н; Н;

Визначити: зусилля в стержнях 1 - 6.

Розв’язання. 1. Розглянемо рівновагу вузла К, у якому сходяться стержні 1, 2, 3 (див. рис. 26.17). На вузол діють задані сили і та реакції стержнів, які покажемо вздовж стержнів від вузла, вважаючи стержні розтягнутими.

Складемо рівняння рівноваги:

(1)

(2)

(3)

З рівняння (3) визначимо:

Н.

З рівняння (1) знайдемо:

Н.

З рівняння (2) одержимо:

Н.

2. Тепер розглянемо рівновагу вузла Н.

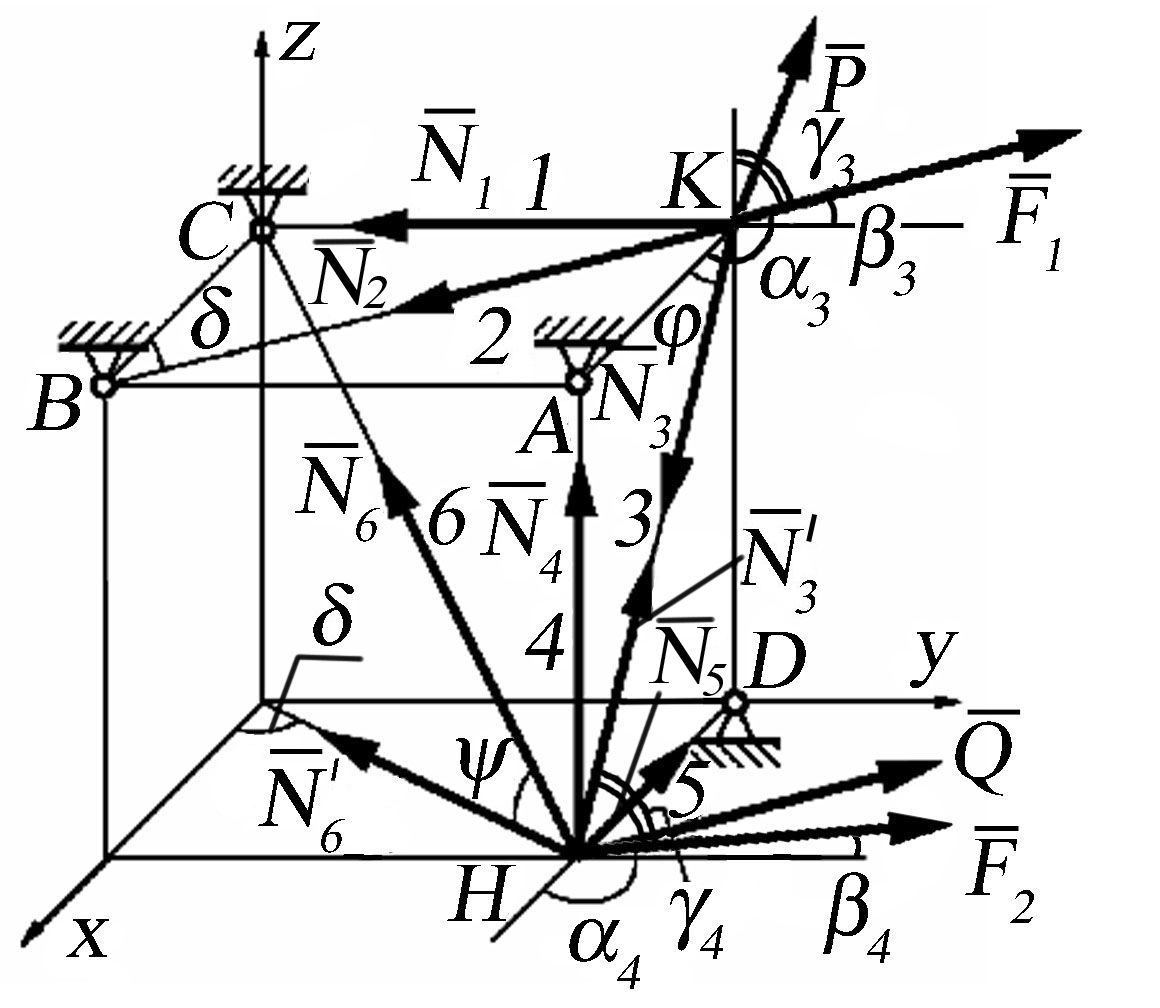
Н

Рис. 26.17

а вузол діють задані сили і та реакції стержнів (див. рис. 26.17). При цьому за законом про рівність дії та протидії реакція має напрямок, протилежний до , а за величиною . Слід зазначити, що при визначенні проекції сили на осі x i y зручніше спочатку знайти проекцію цієї сили на площину xy (за величиною ), а потім цю проекцію на площину проектувати на осі. Складемо рівняння рівноваги:

(4)

(5)

(6)

З рівняння (5) визначимо:

Н.

З рівняння (4) знайдемо:

Н.

З рівняння (6) одержимо:

Н.

Відповідь: Н;Н;Н;

Н;Н; Н.

Знаки показують, що стержні 2, 4 і 5 стиснуті, а інші – розтягнуті.

196