Рисунки до задач с.1.0 – с.1.5

Рисунки до задач с.1.6 – с.1.9

Розв’язання. Розглянемо рівновагу пластини. Проведемо координатні осі ху і покажемо діючі на пластину сили: задані сили ,і пару сил з моментомМ, натяг троса (Т=Р) та реакції в’язей ,. При цьому реакцію нерухомої шарнірної опориА зображаємо двома її складовими ; реакціюшарнірної опори на котках B направляємо перпендикулярно до опорної площини.

Рис. 26.2

Таблиця 3

Умови задач С.1.0.Б – С.1.9.Б

(оцінка п’ять балів)

З рисунка знаходимо:

Номер умови	Значення моменту кН.м
0	- 45
1	+ 40
2	- 38
3	+ 25
4	- 40
5	- 25
6	- 15
7	- 25
8	+ 35
9	- 50

кН.

На пластину діє довільна плоска система сил. Для знаходження невідомих реакцій складаємо три рівняння рівноваги:

(1)

(2)

(3)

Розв’язання системи рівнянь (1) - (3) починаємо з рівняння (3), яке містить одну невідому величину – реакцію опори В . Підставимо в (3) числові дані, одержимо:

кН.

З рівняння (1) маємо:

кН.

З рівняння (2) одержуємо:

кН.

Перевірка. Для перевірки одержаних результатів складаємо рівняння моментів сил відносно точки С, бо в це рівняння увійдуть моменти реакцій ,,:

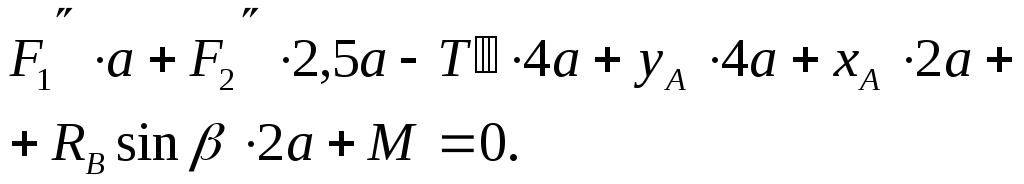
Підставимо числові дані в це рівняння та одержимо:

Результат показує, що реакції опор знайдені правильно.

Відповідь: = - 23,904 кН; = - 25,347 кН;= = - 22,396 кН.

Знаки показують, що сили ,інаправлені протилежно показаним на рис. 26.2.

Приклад розв’язання задачі С.1. Другий рівень складності

Жорстка невагома пластина АВСD (рис. 26.3) закріплена в точці А нерухомою шарнірною опорою, а в точці В - опорою на котках.

У точці D до рами прив’язано трос, перекинутий через нерухомий блок. До іншого кінця троса прикріплено тягар ваги

Р=20 кН. На раму діють: пара сил, абсолютна величина моменту якої дорівнює М=50 кН·м, сила під кутом 60⁰ до горизонту, яка прикладена в точці H, сила , прикладена в точціЕ під кутом 45⁰ до горизонтальної осі, і сила , прикладена під кутомв точціК. Задані розміри та кути показано на рис. 26.3.

Дано: F₁=25 кH;; F₂=40 кH; ;;

; M=50 кHм; P=20 кH; a =0,5 м; F₅=50 кH; .

Визначити: реакції в точках А і В, що обумовлені діючими навантаженнями.

Рис. 26.3

Розв’язання. Розглянемо рівновагу пластини. Проведемо координатні осі і покажемо діючі на пластину сили: задані силиі, пару сил з моментом, натяг троса (за модулем Т=Р) і реакції в’язей ,. При цьому реакцію нерухомої шарнірної опори А зображаємо двома її складовими ; реакціюшарнірної опори на коткахВ направляємо перпендикулярно до опорної площини.

З рисунка знаходимо:

кН;

кН;

кН;

кН;

кН; кН.

Для одержаної плоскої довільної системи сил складемо три рівняння рівноваги :

(1)

(2)

(3)

Проведемо обчислення реакцій. 3 рівняння (3) одержимо:

кН.

З рівняння (2) одержимо:

кН.

З рівняння (1) одержимо:

кН.

Перевірка. Для перевірки одержаних результатів складемо рівняння моментів сил відносно точки С.

Результат показує, що реакції опор знайдені правильно.

Відповідь: = 22,488 кН;= - 31,597 кН;

=65,179 кН.

Знаки показують, що сили інаправлені протилежно показаним на рис. 26.3.

Приклад розв’язання задачі С.1. Третій рівень складності

Жорстка невагома пластина АВСD (рис. 26.4) закріплена в точці А нерухомою шарнірною опорою, а в точці В - опорою на котках.

У точці D до рами прив’язано трос, перекинутий через нерухомий блок. До іншого кінця троса прикріплено тягар ваги

Р=20 кН. На раму діють: пара сил, абсолютна величина моменту якої дорівнює М=50 кН·м, сила під кутом 60⁰ до горизонту, яка прикладена в точці H, сила , прикладена в точціЕ під кутом 45⁰ до горизонтальної осі, і сила , прикладена під кутому точціК. Додатково до рами прикладена пара сил з моментом М₁= - 30 кН·м. Задані розміри та кути показано на рис. 26.4.

Дано : F₁=25 кH;; F₂=40 кH; ;; ; M=50 кHм; P=20 кH; a =0,5 м; F₅=50 кH; ;М₁= - 30 кН·м.

Визначити: реакції в точках А і В, що обумовлені діючими навантаженнями.

Рис. 26.4

Розв’язання. Розглянемо рівновагу пластини. Проведемо координатні осі і покажемо діючі на пластину сили: задані силиі, пари сил з моментамиі(знак моментувраховуємо напрямком дугової стрілки), натяг троса(за модулем) і реакції в’язей ,. При цьому реакцію нерухомої шарнірної опори А зображаємо двома її складовими ; реакціюшарнірної опори на коткахВ направляємо перпендикулярно до опорної площини.

З рисунка знаходимо:

кН;

кН;

кН;

кН;

кН;

кН.

Для одержаної плоскої довільної системи сил складемо три рівняння рівноваги :

(1)

(2)

(3)

Проведемо обчислення реакцій. З рівняння (3) одержимо :

кН.

З рівняння (2) одержимо :

кН.

З рівняння (1) одержимо:

кН.

Перевірка. Для перевірки одержаних результатів складемо рівняння моментів сил відносно точки С.

Результат показує, що реакції опор знайдені правильно.

Відповідь: = 31,148 кН;= - 16,597 кН;

= - 82,5 кН.

Знаки показують, що сили і направлені протилежно показаним на рис. 26.4.

140