8 Геометричні поверхні
В нарисній геометрії поверхні розглядають як результат послідовних положень однієї лінії (твірної) при її переміщенні вздовж іншої лінії (направляючої).
Лінія лежить на поверхні, якщо вона проходить через дві, або більше, точок цієї поверхні.
Точка належить поверхні, якщо вона належить лінії, що знаходиться на поверхні.
8.1 Побудувати відсутні проекції точок, які знаходяться на поверхнях.
9 Перетин поверхонь площиною та прямою
При перетині граної поверхні площиною утворюється замкнута ламана лінія. Для побудови її проекцій визначають точки перетину січної площини з кожним ребром поверхні або лінії перетину граней багатогранника з площиною.
Результатом перетину поверхні обертання площиною є замкнута крива лінія. Для її побудови використовують допоміжні січні площини (рівня або проекцюючі) або твірні (конуса, циліндра).
9.1 Побудувати проекції лінії перетину поверхонь площинами.
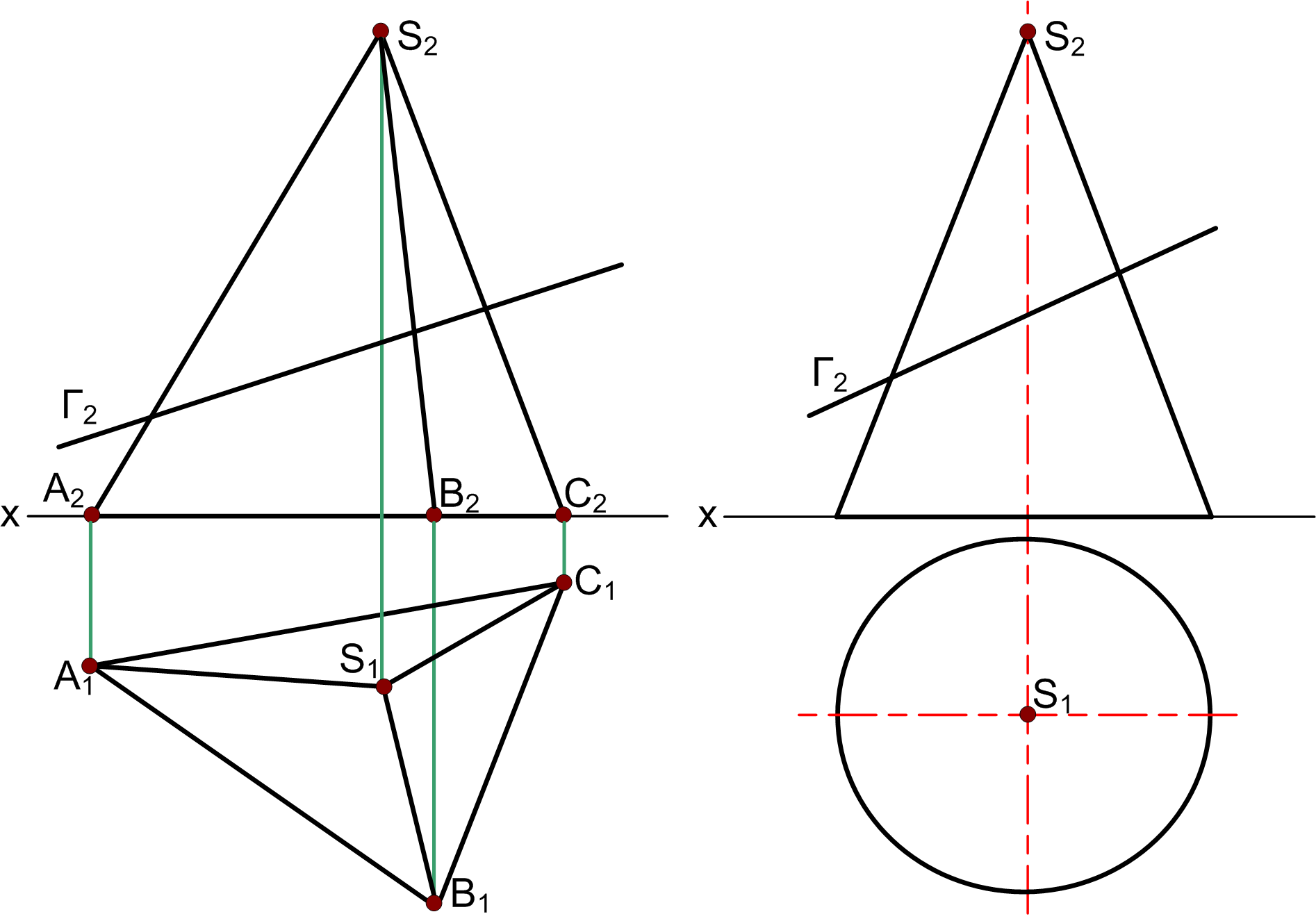
9.2 Побудувати проекції та визначити натуральну величину фігури перерізу піраміди площиною Г.
Результатом перетину прямої та поверхні є дві точки – вхідна та вихідна. Для визначення цих точок необхідно:
пряму заключити у допоміжну січну площину (проекцюючу);
визначити лінію перетину поверхні та допоміжної площини;
позначити точки перетину заданої прямої та лінії перетину.
9.3 Визначити проекції точок перетину прямої l з поверхнею. Визначити видимість.
10 Взаємний перетин поверхонь. Розгортки
Перетин граних поверхонь. При перетині граних поверхонь необхідно побудувати замкнуту ламану лінію, що належить обом поверхням. Для цього визначають точки перетину ребер одного багатогранника з гранями іншого або будують лінії перетину граней поверхонь.
Перетин поверхонь обертання. Для знаходження лінії перетину використовують два методи:
метод допоміжних січних площин рівня;
метод допоміжних січних концентричних сфер, який використовується за наступних умов:
обидві поверхні є поверхнями обертання;
осі симетрії поверхонь перетинаються;
осі, що перетинаються, утворюють площину симетрії поверхонь і паралельна одній з площин проекцій.
10.1 Побудувати проекції лінії перетину поверхонь.
Розгортка – це фігура, яка утворюється при суміщенні геометричної поверхні з площиною без складок і розривів.
10.2 Побудувати розгортки поверхонь з урахуванням фігури перерізу.
11 Зображення: види, розрізи, перерізи, виносні елементи (гост 2.305-68)
11.1 Побудувати відсутні зображення поверхонь з наскрізними призматичними отворами. Виконати необхідні розрізи.
11.2 Побудувати фронтальний (а) та горизонтальний (б) розрізи.
а) б)
11.3 Побудувати ступінчатий розріз.
11.4 Побудувати місцеві розрізи та винесені перерізи.
12 Аксонометричні проекції
Аксонометричні проекції використовують для побудови наочних (об’ємних) зображень геометричних образів та технічних деталей. Аксонометричні зображення будують на основі ортогонального креслення.
Ізометрія. Ізометричні вісі X’, Y’, Z’ розташовані під кутами 120º. Коефіцієнт спотворення лінійних розмірів за осями X’, Y’, Z’: Kx’=Ky’=Kz’.
Диметрія. Відносно лінії горизонту вісь Х’ розташована під кутом 7º10’, вісь Y’ - 41º25’. Коефіцієнт спотворення лінійних розмірів за осями X’, Y’, Z’: Kx’=Ky’=1; Kz’=0,5. тобто всі лінійні розміри за віссю Y’ необхідно зменшувати в два рази.
12.1 Побудувати ізометричну проекцію геометричних фігур.
12.2 Побудувати диметричну проекцію геометричних фігур попередньої задачі.
12.3 На основі ортогонального креслення побудувати ізометрію та диметрію з вирізом четвертої частини по осях X’, Y’.
