Умови завдання:

Визначити загальний об’єм в’їзної та розрізної траншей проведених з наступними параметрами: Н_тр – глибина траншеї; В_тр – ширина траншеї по підошві; α_тр – кут відкосу бортів траншей; і – поздовжній похил в’їзної траншеї; L_р.тр. – довжина розрізної траншеї. Навести та пояснити виведення відповідних формул. Виконати пояснювальну схему на форматі А4, аналогічну до наведеної на наступній сторінці.

варіант	Нтр, м	Втр, м	αтр, °	і, ‰	Lр.тр., м	варіант	Нтр, м	Втр, м	αтр, °	і, ‰	Lр.тр., м
1	10	20	50	35	300	14	15	20	60	90	350
2	15	22	55	28	350	15	12	22	62	95	400
3	12	24	57	45	400	16	18	24	54	45	250
4	18	28	60	40	250	17	20	28	58	60	280
5	20	26	62	42	280	18	22	26	59	43	360
6	22	20	54	36	360	19	10	20	50	58	440
7	10	22	58	44	440	20	15	22	55	69	350
8	15	24	59	48	350	21	12	24	57	80	400
9	12	28	61	50	400	22	18	28	60	100	250
10	18	26	64	55	250	23	20	26	62	39	300
11	20	26	55	70	280	24	22	26	55	59	330
12	22	20	57	45	360	25	15	20	51	60	480
13	15	22	60	85	440

Виведення формул

1. Розглянемо капітальну траншею, як сукупність простих геометричних фігур обсягами V_к.тр. = V₁ + V₂ +V₃.

Фігура обсягом V₁ являє собою призму з основою у вигляді прямокутного трикутника площею S_тр1 та висотою В_тр. Як відомо, площа прямокутного трикутника дорівнює половині добутку катетів. У даному трикутнику нам відомий поздовжній похил i, який дорівнює тангенсу куту між прилеглим катетом та гіпотенузою (у тисячних, тобто, наприклад, і=35‰=0,035), та протилежний катет, який дорівнює Н_тр.

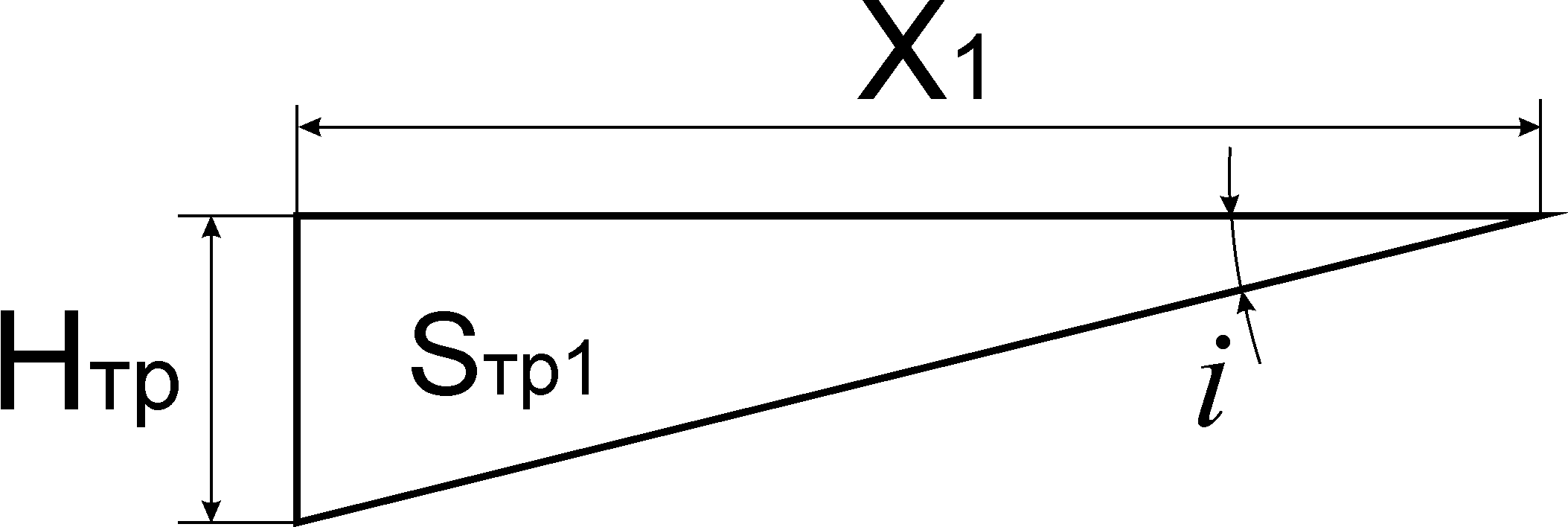Тоді прилеглий катет Х₁ знайдемо, як ,

а площу трикутника .

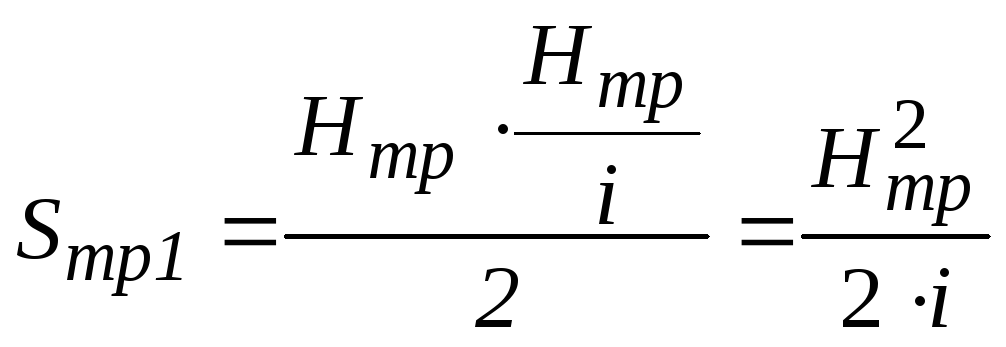Об’єм фігури

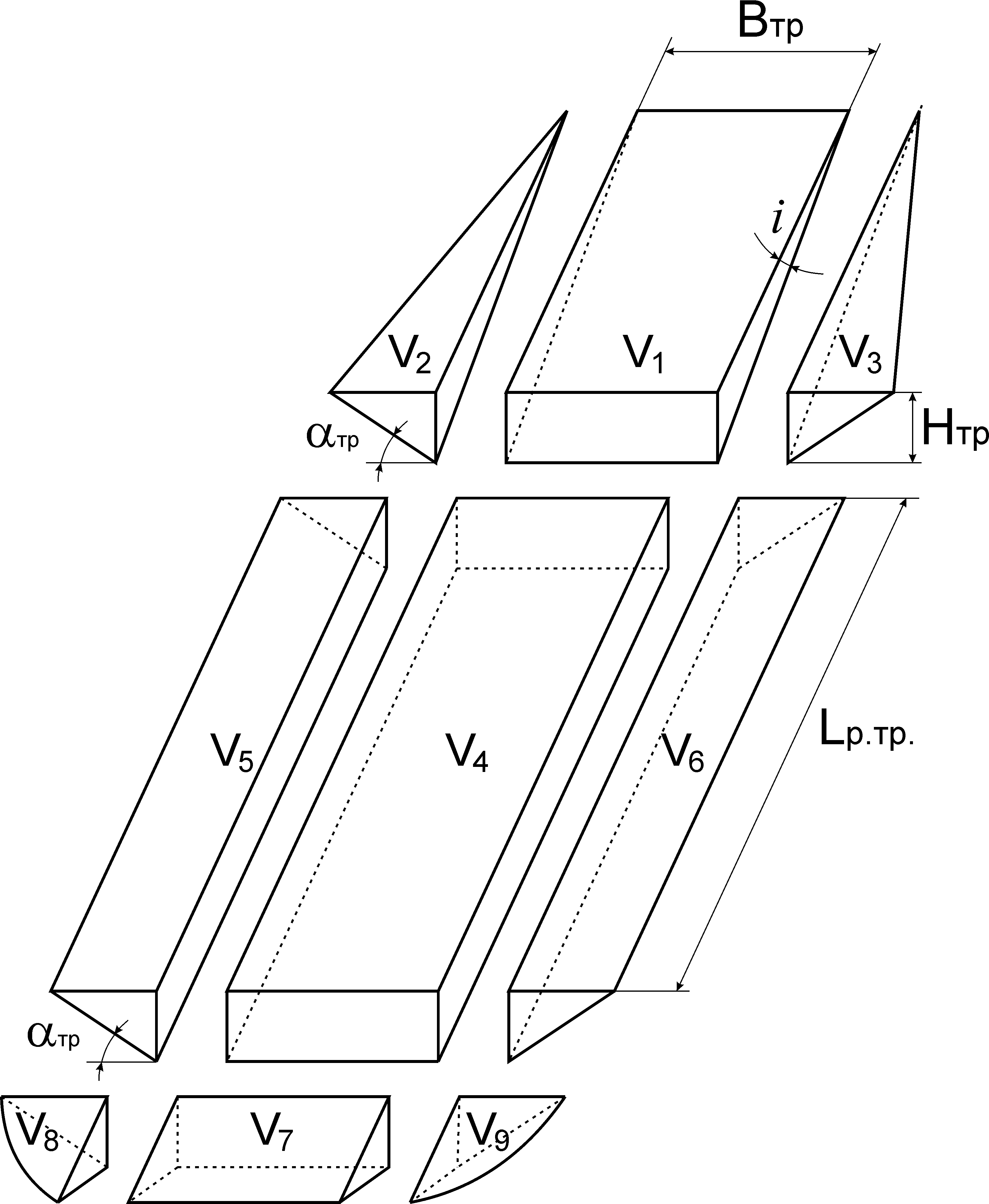
Пояснювальна схема до лабораторної роботи №8

Фігури об’ємом V₂ та V₃ – однакові та являють собою піраміду з основою у вигляді прямокутного трикутнику площею S_тр2 та висотою, якою буде вже знайдена нами раніше величина Х₁.

Р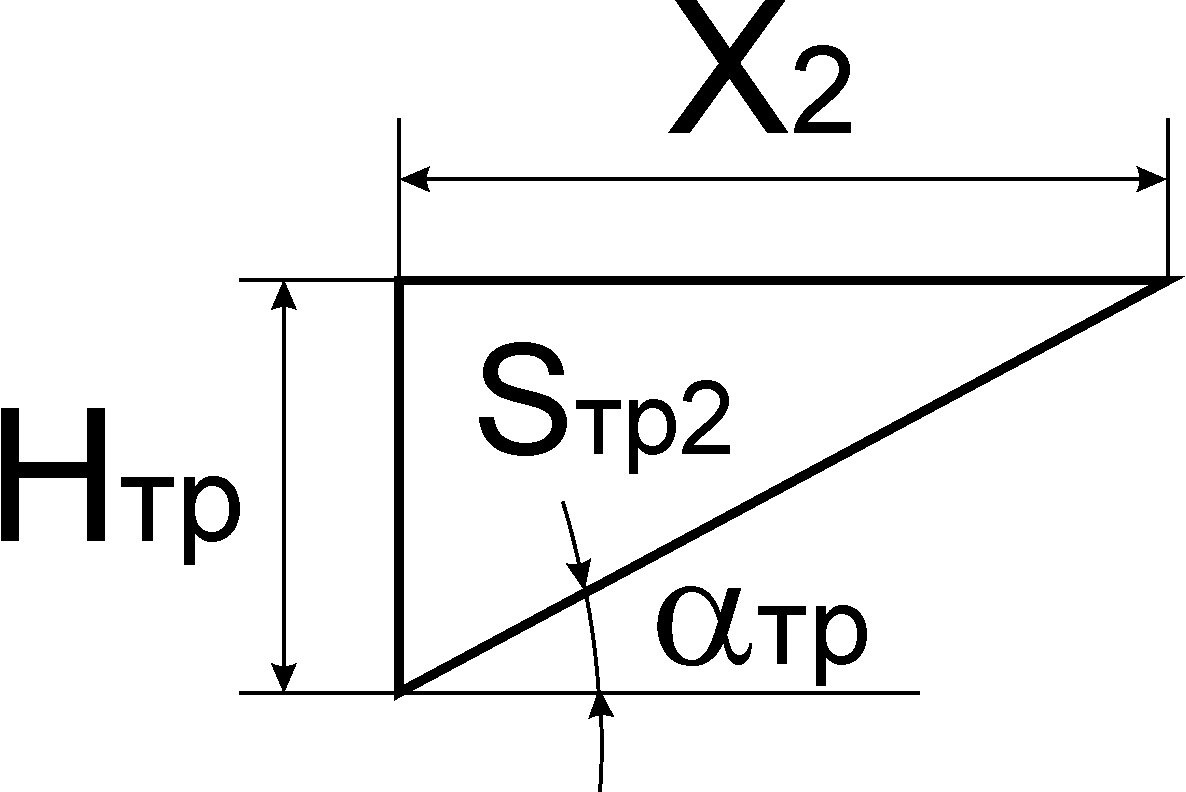озраховуємо площу трикутникуS_тр2, для якого відомо, що зовнішній кут α_тр є внутрішнім кутом, до якого протилежним буде катет Н_тр.

Тоді прилеглий катет Х₂ знайдемо, як ,

а площу трикутника .

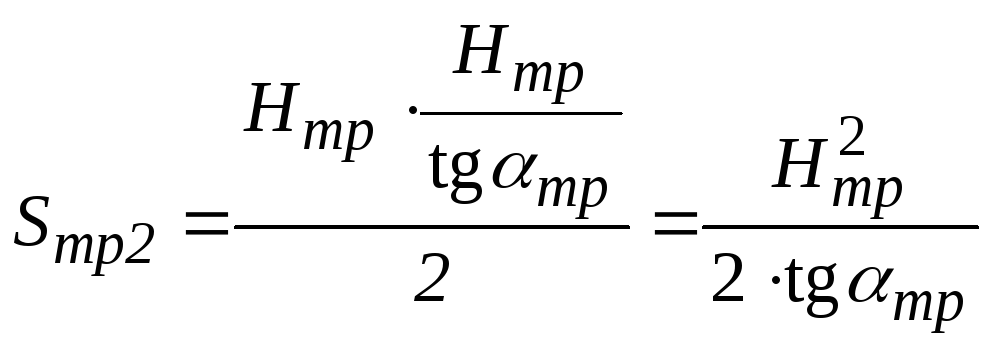Об’єм фігури

Разом об’єм капітальної траншеї:

V_к.тр.=V₁+2∙V₂=, м³.

2. Розглянемо розрізну траншею, як сукупність простих геометричних фігур обсягами V_р.тр. = V₄ + V₅ +V₆.

Фігура обсягом V₄ являє собою паралелепіпед зі сторонами В_тр, Н_тр, L_р.тр. Її об’єм визначити просто: V₄ = В_тр∙Н_тр∙L_р.тр..

Фігури об’ємом V₅ та V₆ також є однаковими та являють собою призми з основою у вигляді прямокутного трикутника площею S_тр2 та висотою L_р.тр, а їх обсяг:

.

Тоді об’єм розрізної траншеї складе:

V_р.тр. = V₄ +2∙ V₅ = В_тр∙Н_тр∙L_р.тр.+ Н_тр∙L_р.тр.∙ , м³.

3. Розглянемо торцеву частину розрізної траншеї, як сукупність простих геометричних фігур об’ємами V_тор.тр. = V₇ + V₈ +V₉.

Фігура об’ємом V₇ являє собою призму з основою у вигляді прямокутного трикутника площею S_тр2 та висотою В_тр:

Фігури об’ємом V₈ та V₉ разом являють половину конуса, основою якого є коло радіусом , а висотою є Н_тр . Тоді 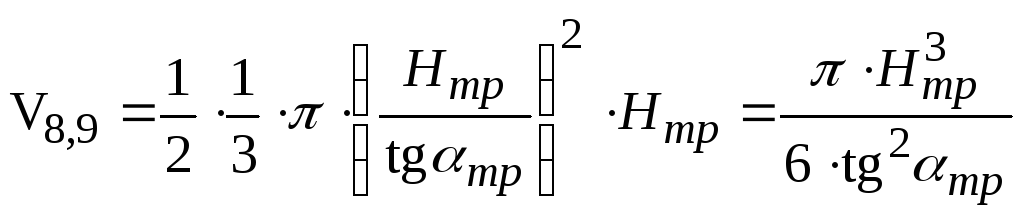,м³.

Отже, V_тор.тр.=V₇+V_8,9=, м³.