Кванти - теорія та розвязки деяких задач

ˆ

2

* d 2

2

d

2

T

dx

dx .

2m

dx2

2M

dx

n 2 , волновая функция осциллятора при

x

, где

x0

m

x0

2

x0

1

e

,

4 2 2 .

2 H

H

2

2

2

22 2!

Подставим явный вид функции в формулу

2

2

ˆ

d

2

2

T

e

4 2

dx ,

16

d

ˆ

e

2

4

6

20

4

25

2

dx .

T

4

Эти интегралы легко взять, если к интегралу Пуассона

2

e x

dx

применить интегрирование по параметру

k

2

2

1 3 ...

2k 1

x2k e x dx

e x dx

,

2k

2k 1

то

ˆ

5

E2

T

4

2

.

ˆ

5

Ответ:

T

4

.

m 2

.

p2

m 2 x2

p 2

x 2

E

2m

2

2m

2

2

2

Из соотношения неопределенностей x

4 p 2

p 2

m 2 2

.

E

2m

8 p 2

Найдем минимум энергии, как функции

p 2

:

1

m 2 2

m

2

0 , p

,

2m

2

2

2

8

p

тогда среднее значение энергии

m

2m 2

2

E

.

4m

8m

2

2

d 2 x

m 2 x2

x q x x E x .

2m dx2

2

m 2

2

2q

q

2

q2 2

U

x

x

m 2

2m 2

2

m 2

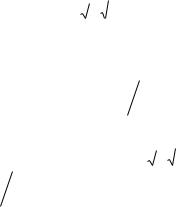
m 2

q 2

q2

2

m 2

x

2

q2 2

x

,

m 2

2m 2

2m 2

2

2

где сделана замена x x

q

, тогда уравнение с учетом заме-

m 2

ны E E

q2 2

примет вид:

2m 2

d 2 x

2

m 2 x 2

x E x ,

2m dx 2

2

решение которого известно:

x

2

E

2n 1 ,

0

e 2 H

.

n

n

n

2

4

2n n!

2n 1

q2

2

x0

2

,

Ответ: E

n

,

n

e

2 H

n

2

2m 2

4 2n n!

x

q

где

x

x0 .

x0

m 2

U

0

a;

a.

Частица не может находиться вне потенциальной ямы, следо-

вательно, волновая функция при

a равна нулю. Граничное

условие для волновой функции:

a 0 .

Уравнение Шредингера для данной частицы

ˆ

ˆ

ˆ2

Lz

H E ,

где

H

.

2m 2

Поскольку операторы

ˆ

и

ˆ

коммутируют, а от координа-

H

Lz

ты z потенциальная энергия не зависит,

то решение уравнения

Шредингера в цилиндрических координатах

2

1

1 2

2

E

2M

2

2

z

2

ищем в виде

, , z eim ,

2

1

m2

E

2M

2

или

1

m2

2

2ME

0 .

2

2

2

Решение этого уравнения CJ

2ME

– функция Бессе-

m

2

2ME

Из граничного условия J

a

0

получаем энергети-

m

2

K

L2z

,

2J

ˆ

i

,

Lz

тогда оператор Гамильтона

ˆ2

2

2

ˆ

Lz

H

.

2J

2J

2

имеет решение

Ceim ,

m

где

m2

2JE

. С

учетом периодичности функции

2

2

m 0,

1,

2, ... Тогда уровни энергии

Em

2 m2

.

2J

Все уровни, кроме основного m 0 , являются дважды вы-

m

Ceim и

m

Ce im .

Пронормируем функцию

2

2

1

1

m

2 d

C

2

2 , откуда C

d 2

C

.

2

0

0

Ответ: E

2 m2

,

e

im

.

m

m

2J

2

ˆ

1