Дослід Кулона. Закон Кулона.

З-н Кулона - основной закон электростатики, позволяющий рассчитать силу взаимодействия между двумя точечными неподвижными зарядами в вакууме. Открыт в 1785 г. французским физиком Шарлем Огюстеном Кулоном.

Опыт Кулона. Металлические шарики заряжаются и взаимодействуют. Заряд измеряется в относительных единицах. Нить закручивается. Сила упругости нити уравновешивает электрическую силу. По углу закручивания нити определяют силу взаимодействия.

1.q2=const, r=const => F ~ q1

2.q1=const, r=const=> F ~ q2

3.q1=const,q2=const=>F ~1/r²

Вывод: Сила взаимодействия двух точечных неподвижных зарядов в вакууме прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между ними.

Сила центральна. Направлена по прямой, соединяющей заряды

F=Коэффициент k зависит от выбора системы единиц.

Коэффициент k численно равен силе взаимодействия между двумя точечными неподвижными зарядами по единице заряда каждый, находящимися в вакууме на расстоянии, равном единице длины друг от друга.

В СИ удобно представить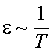

где ε₀=8,85.10^-12 Кл²/(Н*м²) - электрическая постоянная вакуума.

k=9*10⁹(H*м²/Кл²)

Поверхневі і об’ємні поляризаційні заряди, їх зв’язок із вектором поляризації.

Кількісною характеристикою явища поляризації може бути поверхнева густина зв’язаних зарядів σ’.

Знайдемо зв’язок між цими величинами.

В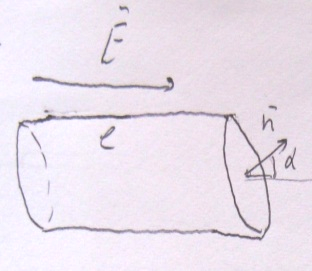ізьмемо однорідне електричне полеE і помістимо в нього діелектрик у формі циліндра, довжина твірної котрого l, площина основи S, кут між твірною і ортом нормалі до основи α. Нехай твірна циліндру паралельна вектору E.

Поляризація приводить до появи на поверхні основ зарядів  і q’= σ’S_i-q’ Циліндр має дипольний момент p=q’l= σ ‘Sl. Вектор поляризації в циліндрі буде направлений вздовж вектора E. За визначенням P маємо: p=PV, де V— об’єм циліндра.

Таким чином, σ’Sl=PSlcos α звідки σ’=Pcos α=P_n=(Pn), де де P_n —складова вектора P вздовж нормалі до поверхні.

Вже було сказано, що в об’ємі діелектрику поля диполів взаємно компенсують одне одного і можна не враховувати поляризаційні заряди. Але це справедливо тільки для однорідно поляризованих діелектриків.Нехай поле E однорідне, але густина діелектрику змінюється від точки до точки. Тоді, взявши замкнену поверхню, яка проходить через атоми або молекули речовини, ми знайдемо в ній поляризаційний заряд. Ми дійдемо висновку, що у подібних випадках треба ввести додатково поняття про об’ємну густину зв’язаних зарядів ρ’.

Знайдемо зв’язок між ρ’ і вектором P.

Візьмемо діелектрик і помістимо його в електричне поле E. Всередині діелектрика проведемо поверхню S, яка проходить через атоми речовини і відокремлює об’єм V.. Тоді в цій області зв’язаний заряд. Тепер звернемо увагу на те, що якщо атом лежить всередині відокремленого об’єму V, то ніякого вкладу в q’ він не вносить. Атом, який лежить на поверхні, посилає всередину поверхні заряд. Тому q’ можна знайти, підсумовуючи по поверхні S  величини σ’=(Pn). Необхідно тільки врахувати, що там, де (Pn)>0, всередину поверхні входить від’ємний заряд і

σ ‘>0 і навпаки, там, де (Pn)<0,тому

таким чином

Перетворюючи ,

одержимо:

звідки маємо ρ’=-divP.