Відносний характер електричних і магнітних полів

Заряд движется в вакууме магнитном поле. С точки зрения наблюдателя, неподвижного относительно поля на заряд действует сила F=q*v*B*sin(v, B). B =мю0*H индукция магнитного поля. V = скорость движения заряда относительно маг. поля, направленного по правилу буравчика.

Представим второго наблюдателя, движущегося вместе с зарядом. Заряд для него неподвижен, но на заряд действует та же сила F, но заряд неподвижен. Это значит что есть электрическое поле. Его напряженность E=F/q=v*B*sin(v,B). Если же это поле (Е) движется относительно наблюдателя, то появится еще и магнитное поле. Т.е. эл-маг поле зависит от системы отсчета. Если в одной есть магнитное поле то в другой есть и магнитное, и электрическое поле. относительный характер – для полей важна относительная скорость. Подтверждение опыт Эйхенвальда:

Рассмотрим конденсатор(??!!) неподвижный относительно земли, тогда если важно абсолютное движението в виду вращения Земли (30 км/с) вокруг конденсатора(??!!) должно образовываться магнитное поле. Оценим величину d=1cm, U = 104B, sin(v,D)=1

D*епсилон0=8,85*10-6 Кл/м2 H=

v*D=30 *103 *8.85*10-6 1/3 А/м.

Если важно относительное движение, то магнитного поля не будет. Опыт показывает отсутствие магнитного поля.

Поляризація густи газів, рідин та твердих тіл. Поле Лоренца. Формула Лоренц-Лоренца.

Для окремого атому раніше було записано дипольний момент , де  — поляризовність,  — поле в діелектрику. Простий аналіз виявляє помилку в цих міркуваннях. Поле в діелектрику є сума зовнішнього поля  і усередненого по простору і в часі поля зв’язаних зарядів, тобто поля всіх диполів, з яких складається діелектрик, включаючи і той диполь, для якого ми обчислюємо . Сам диполь на себе не діє. Замість  в формулу необхідно підставити так зване діюче або локальне поле . Це поле є векторна сума зовнішнього поля  і поля всіх інших диполів, виключаючи вибраний нами:

де  — дипольний момент i–ого диполя, а  — радіус-вектор, проведений з точки, де він знаходиться, в точку, де ми знаходимо  . Штрих в сумі показує, що поле диполя, який знаходиться в точці О, не враховується.Далі буде показано, що для густих газів, рідин та твердих тіл  і  помітно відрізняються, для розріджених газів Обчислення  є достатньо складною задачею. Лоренц запропонував метод, який дозволяє обчислити діюче поле для газів, рідин і кубічних кристалів. Для кристалів не кубічних сингоній цей метод незастосовний. Розглянемо суть методу Лоренца. Лоренц запропонував оточити точку О, в якій ми обчислюємо , сферою такого радіусу, щоб в ній знаходилося багато диполів. Вилучимо речовину діелектрика, яке знаходиться у сфері. В діелектрику утвориться порожнина. Поле всередині неї можна обчислити, вважаючи, що поля всіх диполів, які залишились в об’ємі, компенсують одне одного.Тоді поле в порожнині складається з , поля поляризаційних зарядів на поверхні діелектрика  і поля поляризаційних зарядів на поверхні сферичної порожнини :Але , де  — поле в діелектрику, , як було показано вище, тому Тепер треба врахувати ті диполі, які знаходяться всередині видаленої нами кулі, вони дають поле , яке треба обчислити. Тоді:

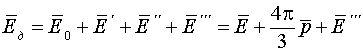
Лоренц показав, що для газів, рідин та кубічних кристалів , тому

Доведемо, що . Розглянемо кристал з кубічною граткою.

сума береться по всіх диполях в межах сфери, виключаючи диполь в точці О. Відкинемо індекс , виберемо початок координат в точці О. Тоді, взявши проекцію на вісь , маємо:

Розглянемо суму

Нехай в кубічному кристалі всередині сфери в точці  знаходиться диполь, тобто ця точка — вузол кубічної гратки. Тоді точка  також належить гратці і в ній знаходиться диполь. У вибраній нами сумі доданки, що відносяться до цих двох точок, взаємно скоротяться. Так можна поступити з усіма точками всередині сфери, в яких знаходяться диполі, і показати, що Для рідин і газів результат буде таким же, треба лише, вибравши точку , врахувати, що в точці  з тією ж імовірністю буде знаходитись диполь. Аналогічно доводиться рівність нулю всіх інших сум. Для  треба лише точці  зіставити точку , в сумі  — точку , і т.п. Показавши, що , подібним чином можна одержати  і . Отже, . Визначивши , можна записати:, ,

звідки Але , тоді

Формула Лоренц-Лоренца. Концентрація  пов’язана із середньою відстанню  між частинками співвідношенням , поляризовність , де  — радіус атому, . Для розріджених газів , тому , , , тобто ми одержали попередній результат, відповідно, . Для густих газів, рідин та твердих тіл , тому необхідно враховувати різницю між  і .