
- •Теорема Остроградського-Гаусса.
- •Скін-ефект
- •Умова виникнення самостійного газового розряду. Плазма газового розряду
- •Експериментальна перевірка закону Кулона. Теоретичне обґрунтування досліду Кавендіша.
- •Експериментальна перевірка закону Кулона. Теоретичне обґрунтування досліду Кавендіша.
- •Температурна залежність намагніченості феромагнетиків. Закон Кюрі - Вейсса.
- •Труднощі теорії Друде-Лоренца.
- •Дослід Кулона. Закон Кулона.
- •Поверхневі і об’ємні поляризаційні заряди, їх зв’язок із вектором поляризації.
- •Теорема Пойтінга.
- •Теорема Ірншоу.
- •2.Природа діамагнетизму. Теорема Лармора.
- •3.Термоелектронна, автоелектронна і фотоелектронна емісія.
- •Електростатичний Генератор Ван-де-Граафа
- •Електростатичний Генератор Ван-де-Граафа
- •Електростатичний Генератор Ван-де-Граафа
- •Теорія Ланжевена оріентаційпої поляризації газів зі сталим дипольним моментом.
- •Теорія Ланжевена оріентаційпої поляризації газів зі сталим дипольним моментом.
- •Формула Річардсона-Дешмана
- •Провідники в електростатичному полі.
- •Провідники в електростатичному полі.
- •Закон Джоуля-Ленца в інтегральній та диференціальній формі
- •Закон Джоуля-Ленца в інтегральній та диференціальній формі
- •Довести поперечність електромагнітної хвилі
- •Взаємна енергія двох диполів.
- •Вплив форми та розміру тіла ан його магнітні властивості. Поле розмагнічування.
- •Закон Джоуля-Ленца в класичній електронній теорії металів Друде-Лоренца.
- •Еквівалентність виразів для електростатичного поля для випадків її локалізації у місці знаходження розподіленого заряду та наявності електростатичного поля.
- •Вектор-потенціал магнітного поля
- •Умова виникнення самостійного газового розряду. Плазма газового розряду.
- •Класична теорія поляризації газів.
- •Закон електромагнітної індукції Фарадея. Правило Ленця.
- •Закон Відемана-Франца в класичній електронній теорії металів Друде-Лоренца.
- •Закон Відемана-Франца в класичній електронній теорії металів Друде-Лоренца.
- •Закон Відемана-Франца в класичній електронній теорії металів Друде-Лоренца.
- •Частотна залежність сумарної діелектричної проникності діелектриків
- •Закон Ампера для магнітної взаємодії струмів в інтегральній і диференціальній формі.
- •Закон Ампера для магнітної взаємодії струмів в інтегральній і диференціальній формі.
- •Закон трьох других
- •Зв'язок між напруженістю електростатичного поля та потенціалом
- •Магнітна сприйнятливість та магнітна проникність
- •Зв’язок енергії електро статичного поля з пондеромоторними силами. Абсолютний вольтметр
- •Закон Біо-Савара-Лапласа в інтегральній і диференціальній формах.
- •Формула Річардсона-Дешмана
- •Формула Клаузіуса-Моссотті. Поляризаційна катастрофа.
- •Самостійний і несамостійний газовий розряд. Основні типи самостійного газового розряду.
- •Електричний диполь. Поле диполя
- •Теорема про циркуляцію вектора напруженості магнітного поля по замкнутому контуру в інтегральній і диференціальній формі.
- •Сегнетоелектрики. Сегнетоелектричні Домени.
- •Знаходження розподілу потенціалу методом електричних зображень.
- •Умови для векторів напруженості магнітного поля і магнітної індукції на межі двох магнетиків.
- •Диференціальна форма запису теореми Остроградського-Гаусса.
- •П’єзоелектричний ефект
- •Вектор електричного зміщення . Диференціальне формулювання теореми Остроградського - Гауса для поля в діелектриках .
- •Діаграма направленості диполя Герца . Залежність потужності випромінювання від частоти .
- •Інваріантність рівнянь Максвелла відносно перетворень Лоренца.
- •Енергія електростатичного поля , її локалізація за наявності розподіленого заряду.
- •Тиск електромагнітних хвиль.
- •Природа носіїв заряду в металах. Досліди Рікке та Томлена і Стюарта.
- •Потенціальний характер електростатичного поля. Інтегральне та диференціальне формулювання потенціальності електростатичного поля.
- •Імпульс електромагнітної хвилі.
- •Вектор електричного зміщення. Диференціальне формулювання теореми Остроградського-Гаусса для поля в діелектриках. © kot
- •Діаграма направленості диполя Герца. Залежність потужності випромінювання від частоти. © kot
- •Електроємність. Конденсатори. Послідовне і паралельне з’єднання конденсаторів.
- •Абсолютна електромагнітна система одиниць та її зв’язок с абсолютною електростатичною системою одиниць. Електродинамічна стала.
- •Швидкість розповсюдження електромагнітної хвилі.
- •Енергія електростатичного поля, її локалізація за рахунок поля.
- •Струм зміщення.
- •Закон Ома в інтегральній і диференциальной формі.
- •Відносний характер електричних і магнітних полів
- •Поляризація густи газів, рідин та твердих тіл. Поле Лоренца. Формула Лоренц-Лоренца.
- •Класична теорія парамагнетизму. Формула Ланжевена і закон Кюрі.
- •Закон Ома в класичній електронній теорії металів Друде-Лоренца
- •Вплив форми та розміру тіла на його магнітні властивості. Поле розмагнічування.
- •Сила Лоренца. Рух заряду в електричному та магнітному полі. Ефект Холла
- •Повна енергія випромінювання диполя Герца. Опір випромінювання
Енергія електростатичного поля, її локалізація за рахунок поля.
Повна енергія
взаємодії с-ми зарядів ![]() ,
де
,
де ![]() потенціал створюваний зарядами в
елементі об’єму
потенціал створюваний зарядами в
елементі об’єму ![]() .
Але енергію W можна також виразити через
величину , що характеризує саме електричне
поле - напруженість Е. У випадку, якщо
діелектрик ізотропний (для якого
виконується співвідношення
.
Але енергію W можна також виразити через
величину , що характеризує саме електричне
поле - напруженість Е. У випадку, якщо
діелектрик ізотропний (для якого
виконується співвідношення ![]() ) енергія
виражається:
) енергія
виражається:

Підінтегральний
вираз має сенс енергії замкненої в
об’ємі ![]() .
Це приводить до ідеї локалізації енергії
поля в самому полі. Дана ідея дослідно
підтверджена в області змінних полів.
(саме змінні поля можуть існувати окремо
від збудивши їх ел. Зарядів і
розповсюджуватись у вигляді хвиль,
дослід показує, що хвилі переносять
енергію).
.
Це приводить до ідеї локалізації енергії
поля в самому полі. Дана ідея дослідно
підтверджена в області змінних полів.
(саме змінні поля можуть існувати окремо
від збудивши їх ел. Зарядів і
розповсюджуватись у вигляді хвиль,
дослід показує, що хвилі переносять
енергію).
Елекрична енергія розподілена в просторі з обємою густиною

Струм зміщення.
Закон збереження
заряду в випадку постійного струму має
вигляд:
 ,
або в диференціальній формі
,
або в диференціальній формі
![]() .
Закон повного в цьому випадку струму
зв’язував струм і створюване ним
магнітне поле:
.
Закон повного в цьому випадку струму
зв’язував струм і створюване ним
магнітне поле:
![]() ,
або
,
або
![]() .
Нехай електричне поле і електричний
струм будуть змінними. Можна показати
неспроможність закону повного струму
в диференціальній формі:
.
Нехай електричне поле і електричний
струм будуть змінними. Можна показати
неспроможність закону повного струму
в диференціальній формі:
![]() ,
візьмемо дивергенцію від обох частин
рівності:
,
візьмемо дивергенцію від обох частин
рівності:![]() ,
,
 Для
того щоб зберегти закон повного струму
і для змінних струмів, Максвелл
запропонував записати його у вигляді:
Для
того щоб зберегти закон повного струму
і для змінних струмів, Максвелл
запропонував записати його у вигляді:![]() де
де
![]() —
густина струму провідності, а доданок
—
густина струму провідності, а доданок
![]() одержав
назву густини струму зміщення
одержав
назву густини струму зміщення
 .
Додавання доданку
.
Додавання доданку
![]() “рятує”
закон повного струму:
“рятує”
закон повного струму:
![]() ,
але
,
але
![]() теж
може дорівнювати нулю, якщо
теж
може дорівнювати нулю, якщо
![]() .
За законом збереження заряду
.
За законом збереження заряду
 ,
тоді:
,
тоді: З
рівнянь Максвелла
З
рівнянь Максвелла
![]() ,
тому:
,
тому: Це
диференціальне рівняння допускає
множину розв’язків. З них Максвелл
вибрав найпростіший:
Це
диференціальне рівняння допускає
множину розв’язків. З них Максвелл
вибрав найпростіший: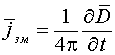
(
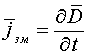 в
системі СІ).
Густина струму зміщення є швидкість
зміни вектору електричної індукції (з
точністю до множника -
в
системі СІ).
Густина струму зміщення є швидкість
зміни вектору електричної індукції (з
точністю до множника -
![]() в
CGSM).
Основним наслідком, який витікає з
гіпотези Максвелла, є те, що вихрове
магнітне поле створюється як струмами
провідності, так і струмами зміщення,
тобто змінними електричними полями.
Рівняння Максвелла, що виражає закон
повного струму, тепер виглядає так:
в
CGSM).
Основним наслідком, який витікає з
гіпотези Максвелла, є те, що вихрове
магнітне поле створюється як струмами
провідності, так і струмами зміщення,
тобто змінними електричними полями.
Рівняння Максвелла, що виражає закон
повного струму, тепер виглядає так:![]() а
в інтегральній формі:
а
в інтегральній формі:

Основна властивість
струму зміщення — створювати вихрове
магнітне поле. Струм зміщення може
існувати в провідниках, діелектриках,
у вакуумі. В тому випадку, коли
![]() ,
два рівняння Максвелла набувають
симетричної форми:
,
два рівняння Максвелла набувають
симетричної форми:![]() ,
,
![]() Змінне
магнітне поле створює вихрове електричне
поле завдяки явищу електромагнітної
індукції, а змінне електричне поле
створює вихрове магнітне.Струм зміщення,
на відміну від струму провідності, не
супроводжується виділенням тепла
Джоуля-Ленца.У випадку провідників,
вздовж яких протікає змінний струм і в
яких існує змінне електричне поле, за
звичай
Змінне
магнітне поле створює вихрове електричне
поле завдяки явищу електромагнітної
індукції, а змінне електричне поле
створює вихрове магнітне.Струм зміщення,
на відміну від струму провідності, не
супроводжується виділенням тепла
Джоуля-Ленца.У випадку провідників,
вздовж яких протікає змінний струм і в
яких існує змінне електричне поле, за
звичай
![]() .
Однак, при збільшенні частоти змінного
струму відносна роль струму зміщення
зростає,
.
Однак, при збільшенні частоти змінного
струму відносна роль струму зміщення
зростає,
![]() може
зрівнятися з густиною струму провідності
і навіть перевищити цю величину.
може
зрівнятися з густиною струму провідності
і навіть перевищити цю величину.
Закон Ома в інтегральній і диференциальной формі.
В отсутствие
электрического поля частицы в проводнике
(которые приближенно можно считать
свободными) совершают хаотическое
движение. Все направления движения
свободных частиц равноправны. Поэтому
усредненные по всему коллективу частиц
проекции скорости равны нулю. Если
проводник находится в электрическом
поле, то на частицы действуют направленные
силы. Если следить за какой-нибудь
частицей, то можно обнаружить, что на
тепловое хаотическое движение частицы
накладывается направленное движение
ее под действием силы со стороны
электрического поля. Рассмотрим движение
одной частицы. заряженная частица с
зарядом е и массой m движется в однородном
электрическом поле. Сила, действующая
на частицу со стороны поля, равна
![]() ,
где
,
где
![]() –
напряженность поля, которую можно
считать постоянной. Тогда уравнение ее
движения имеет вид:
–
напряженность поля, которую можно
считать постоянной. Тогда уравнение ее
движения имеет вид:
![]() .
Если вектор напряженности направлен
по оси Ох, то учкорение тоже направлено
по этой оси и равно
.
Если вектор напряженности направлен
по оси Ох, то учкорение тоже направлено
по этой оси и равно
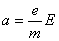 .
Если начальная скорость частицы равна
нулю, то в момент времени t
она равна
.
Если начальная скорость частицы равна
нулю, то в момент времени t
она равна
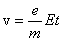 ,
а средняя скорость вдвое меньше, за
некоторый промежуток времени τ она
равна
,
а средняя скорость вдвое меньше, за
некоторый промежуток времени τ она
равна

Будем считать, что
движущиеся заряженные частицы сталкиваются
с другими частицами через одинаковое
время τ, которое можно отождествить со
средним временем между соударениями.
в среднем в результате соударения
частицы останавливаются, а после этого
они снова начинают движение в электрическом
поле с нулевой начальной скоростью. По
этой причине можно считать, что частицы
движутся в электрическом поле со средней
скоростью. Пусть частицы движутся влево
со скоростью v . За время t
они проходят путь, равный l = vt.
Таким образом, за это время сечение S
проводника пересекут только те частицы,
которые отстоят от него на расстояние,
меньшее или равное
l, т.е. те
частицы, которые находятся внутри
цилиндра высотой l = vt
и объема
V = S(vt).
Если концентрация частиц равна n,
то их число в этом объеме равно
N = nV = nS(vt).
Пусть заряд одной частицы равен q.
Тогда за время t
через сечение проводника протекает
суммарный заряд N
частиц, равный Q = qN = qnSvt.
Следовательно, сила тока через проводник
равна
![]() ,
а плотность тока –
,
а плотность тока –
![]() .
Величина j
пропорциональна средней скорости
направленного движения, а именно
j = еnavn.
Подставляя сюда avn
из формулы ускорения получим:
.
Величина j
пропорциональна средней скорости
направленного движения, а именно
j = еnavn.
Подставляя сюда avn
из формулы ускорения получим:
 .
Это выражение
называют законом
Ома в дифференциальной форме.
.
Это выражение
называют законом
Ома в дифференциальной форме.
Величина
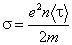 называется
коэффициентом электропроводности или
просто электропроводностью данного
проводника, а коэффициент пропорциональности
между средней скоростью направленного
движения зарядов avn
и напряженностью приложенного
электрического поля Е
называют подвижностью носителей тока.
Из формулы (2) видно, что подвижность
выражается следующим образом:
называется
коэффициентом электропроводности или
просто электропроводностью данного
проводника, а коэффициент пропорциональности
между средней скоростью направленного
движения зарядов avn
и напряженностью приложенного
электрического поля Е
называют подвижностью носителей тока.
Из формулы (2) видно, что подвижность
выражается следующим образом:
 .
Смысл закона Ома заключается в том, что
средняя скорость направленного движения
носителей тока пропорциональна
напряженности электрического поля,
т.е. пропорциональна действующей на
частицы силе. Закон Ома выполняется для
металлов, полупроводников, электролитов,
т.е. для тех веществ, в которых носители
тока испытывают большое число соударений.
При этом данный закон выполняется при
не слишком сильных полях, когда роль
соударений велика. Закон Ома не выполняется
при токах в вакууме, так как в этом случае
носители тока практически не испытывают
столкновений. Закон Ома очень ограниченно
выполняется в плазме, так как в плазме
обычно непостоянно число носителей
тока. Рассмотрим участок однородного
проводника, имеющего для простоты
цилиндрическую форму (рис. 2). Пусть
площадь поперечного сечения проводника
S, а
длина l.
К концам проводника приложена разность
потенциалов U = j1 – j2,
то есть внутри проводника действует
электрическое поле
.
Смысл закона Ома заключается в том, что
средняя скорость направленного движения
носителей тока пропорциональна
напряженности электрического поля,
т.е. пропорциональна действующей на
частицы силе. Закон Ома выполняется для
металлов, полупроводников, электролитов,
т.е. для тех веществ, в которых носители
тока испытывают большое число соударений.
При этом данный закон выполняется при
не слишком сильных полях, когда роль
соударений велика. Закон Ома не выполняется
при токах в вакууме, так как в этом случае
носители тока практически не испытывают
столкновений. Закон Ома очень ограниченно
выполняется в плазме, так как в плазме
обычно непостоянно число носителей
тока. Рассмотрим участок однородного
проводника, имеющего для простоты
цилиндрическую форму (рис. 2). Пусть
площадь поперечного сечения проводника
S, а
длина l.
К концам проводника приложена разность
потенциалов U = j1 – j2,
то есть внутри проводника действует
электрическое поле
![]() .
Поэтому в проводнике возникает
электрический ток, плотность тока,
согласно закону Ома, j = sЕ.
Если ток распределен равномерно по
сечению проводника, то сила тока
I = jS = sES.
.
Поэтому в проводнике возникает
электрический ток, плотность тока,
согласно закону Ома, j = sЕ.
Если ток распределен равномерно по
сечению проводника, то сила тока
I = jS = sES.
В случае однородного
поля напряженность поля Е
связана с
потенциалом соотношением:
![]() .
Поэтому сила тока в проводнике
.
Поэтому сила тока в проводнике
![]() ,
откуда
,
откуда
![]() .
Величина
.
Величина
![]() (удельное
сопротивление
(удельное
сопротивление
![]() )
называется сопротивлением данного
участка проводника. Тогда закон
Ома в интегральной форме
имеет вид: IR
= j1
– j2
= U
)
называется сопротивлением данного
участка проводника. Тогда закон
Ома в интегральной форме
имеет вид: IR
= j1
– j2
= U
