
- •Теорема Остроградського-Гаусса.
- •Скін-ефект
- •Умова виникнення самостійного газового розряду. Плазма газового розряду
- •Експериментальна перевірка закону Кулона. Теоретичне обґрунтування досліду Кавендіша.
- •Експериментальна перевірка закону Кулона. Теоретичне обґрунтування досліду Кавендіша.
- •Температурна залежність намагніченості феромагнетиків. Закон Кюрі - Вейсса.
- •Труднощі теорії Друде-Лоренца.
- •Дослід Кулона. Закон Кулона.
- •Поверхневі і об’ємні поляризаційні заряди, їх зв’язок із вектором поляризації.
- •Теорема Пойтінга.
- •Теорема Ірншоу.
- •2.Природа діамагнетизму. Теорема Лармора.
- •3.Термоелектронна, автоелектронна і фотоелектронна емісія.
- •Електростатичний Генератор Ван-де-Граафа
- •Електростатичний Генератор Ван-де-Граафа
- •Електростатичний Генератор Ван-де-Граафа
- •Теорія Ланжевена оріентаційпої поляризації газів зі сталим дипольним моментом.
- •Теорія Ланжевена оріентаційпої поляризації газів зі сталим дипольним моментом.
- •Формула Річардсона-Дешмана
- •Провідники в електростатичному полі.
- •Провідники в електростатичному полі.
- •Закон Джоуля-Ленца в інтегральній та диференціальній формі
- •Закон Джоуля-Ленца в інтегральній та диференціальній формі
- •Довести поперечність електромагнітної хвилі
- •Взаємна енергія двох диполів.
- •Вплив форми та розміру тіла ан його магнітні властивості. Поле розмагнічування.
- •Закон Джоуля-Ленца в класичній електронній теорії металів Друде-Лоренца.
- •Еквівалентність виразів для електростатичного поля для випадків її локалізації у місці знаходження розподіленого заряду та наявності електростатичного поля.
- •Вектор-потенціал магнітного поля
- •Умова виникнення самостійного газового розряду. Плазма газового розряду.
- •Класична теорія поляризації газів.
- •Закон електромагнітної індукції Фарадея. Правило Ленця.
- •Закон Відемана-Франца в класичній електронній теорії металів Друде-Лоренца.
- •Закон Відемана-Франца в класичній електронній теорії металів Друде-Лоренца.
- •Закон Відемана-Франца в класичній електронній теорії металів Друде-Лоренца.
- •Частотна залежність сумарної діелектричної проникності діелектриків
- •Закон Ампера для магнітної взаємодії струмів в інтегральній і диференціальній формі.
- •Закон Ампера для магнітної взаємодії струмів в інтегральній і диференціальній формі.
- •Закон трьох других
- •Зв'язок між напруженістю електростатичного поля та потенціалом
- •Магнітна сприйнятливість та магнітна проникність
- •Зв’язок енергії електро статичного поля з пондеромоторними силами. Абсолютний вольтметр
- •Закон Біо-Савара-Лапласа в інтегральній і диференціальній формах.
- •Формула Річардсона-Дешмана
- •Формула Клаузіуса-Моссотті. Поляризаційна катастрофа.
- •Самостійний і несамостійний газовий розряд. Основні типи самостійного газового розряду.
- •Електричний диполь. Поле диполя
- •Теорема про циркуляцію вектора напруженості магнітного поля по замкнутому контуру в інтегральній і диференціальній формі.
- •Сегнетоелектрики. Сегнетоелектричні Домени.
- •Знаходження розподілу потенціалу методом електричних зображень.
- •Умови для векторів напруженості магнітного поля і магнітної індукції на межі двох магнетиків.
- •Диференціальна форма запису теореми Остроградського-Гаусса.
- •П’єзоелектричний ефект
- •Вектор електричного зміщення . Диференціальне формулювання теореми Остроградського - Гауса для поля в діелектриках .
- •Діаграма направленості диполя Герца . Залежність потужності випромінювання від частоти .
- •Інваріантність рівнянь Максвелла відносно перетворень Лоренца.
- •Енергія електростатичного поля , її локалізація за наявності розподіленого заряду.
- •Тиск електромагнітних хвиль.
- •Природа носіїв заряду в металах. Досліди Рікке та Томлена і Стюарта.
- •Потенціальний характер електростатичного поля. Інтегральне та диференціальне формулювання потенціальності електростатичного поля.
- •Імпульс електромагнітної хвилі.
- •Вектор електричного зміщення. Диференціальне формулювання теореми Остроградського-Гаусса для поля в діелектриках. © kot
- •Діаграма направленості диполя Герца. Залежність потужності випромінювання від частоти. © kot
- •Електроємність. Конденсатори. Послідовне і паралельне з’єднання конденсаторів.
- •Абсолютна електромагнітна система одиниць та її зв’язок с абсолютною електростатичною системою одиниць. Електродинамічна стала.
- •Швидкість розповсюдження електромагнітної хвилі.
- •Енергія електростатичного поля, її локалізація за рахунок поля.
- •Струм зміщення.
- •Закон Ома в інтегральній і диференциальной формі.
- •Відносний характер електричних і магнітних полів
- •Поляризація густи газів, рідин та твердих тіл. Поле Лоренца. Формула Лоренц-Лоренца.
- •Класична теорія парамагнетизму. Формула Ланжевена і закон Кюрі.
- •Закон Ома в класичній електронній теорії металів Друде-Лоренца
- •Вплив форми та розміру тіла на його магнітні властивості. Поле розмагнічування.
- •Сила Лоренца. Рух заряду в електричному та магнітному полі. Ефект Холла
- •Повна енергія випромінювання диполя Герца. Опір випромінювання
Знаходження розподілу потенціалу методом електричних зображень.
Розглянемо задачу
про знаходження розподілу потенціалу
між провідниками при відсутності
об’ємного заряду, ![]() .
В загальному випадку потрібно розв’язувати
рівняння Лапласа
.
В загальному випадку потрібно розв’язувати
рівняння Лапласа ![]() ,
крайові умови при цьому частіше за все
задають потенціали на провідниках,
поверхні яких є еквіпотенціальними.
Розглянемо метод електричних зображень.
Візьмемо деяку просту електростатичну
задачу, що не потребує вирішення рівняння
Лапласа. Наприклад, це невелика кількість
точкових зарядів. Нехай розподіл
потенціалу нам відомий:
,
крайові умови при цьому частіше за все
задають потенціали на провідниках,
поверхні яких є еквіпотенціальними.
Розглянемо метод електричних зображень.
Візьмемо деяку просту електростатичну
задачу, що не потребує вирішення рівняння
Лапласа. Наприклад, це невелика кількість
точкових зарядів. Нехай розподіл
потенціалу нам відомий: ![]() .
Якщо обрати
.
Якщо обрати ![]() ,
то знайдемо рівняння еквіпотенціальної
поверхні з потенціалом C.
Обираючи різні значення С,
одержимо систему еквіпотенціальних
поверхонь. Оберемо, поверхню
,
то знайдемо рівняння еквіпотенціальної
поверхні з потенціалом C.
Обираючи різні значення С,
одержимо систему еквіпотенціальних
поверхонь. Оберемо, поверхню ![]() .
Якщо тепер взяти тонку металеву фольгу
і вигнути її так, щоб вона співпала з
еквіпотенціальною поверхнею, розмістити
на місце неї подати на фольгу потенціал
.
Якщо тепер взяти тонку металеву фольгу
і вигнути її так, щоб вона співпала з
еквіпотенціальною поверхнею, розмістити
на місце неї подати на фольгу потенціал
![]() , то поле зовні фольги не зміниться. В
той же час фольга слугуватиме екраном,
що розділяє дві сторони. Тепер можна
змінювати як завгодно умови з однієї
сторони фольги, поле з другої сторони
не зміниться. Заллємо металом одну
сторону. Тоді поле по іншу сторону не
зміниться і буде відомим. Тепер має
місце інша електростатична задача:
поверхня провідника з потенціалом C1 і
три точкові заряди над нею. Вирішити цю
нову задачу достатньо складно, тому що
на поверхні провідника є поляризаційні
заряди, розподіл яких необхідно знати.
Між тим задача спрощується, якщо видалити
провідник і в потрібних точках розташувати
три заряди, так аби на поверхні металу
після заміни була розташована
еквіпотенціальна поверхня. У
методі дзеркальних відображень, замість
вирішення задачі про розподіл потенціалу
в системі заряджених провідників і
зарядів над ними, намагаються підібрати
таке розташування точкових зарядів і
таку їх величину, щоб еквіпотенціальні
поверхні співпадали з поверхнею
провідників і мали потрібне значення
потенціалів.
, то поле зовні фольги не зміниться. В
той же час фольга слугуватиме екраном,
що розділяє дві сторони. Тепер можна
змінювати як завгодно умови з однієї
сторони фольги, поле з другої сторони
не зміниться. Заллємо металом одну
сторону. Тоді поле по іншу сторону не
зміниться і буде відомим. Тепер має
місце інша електростатична задача:
поверхня провідника з потенціалом C1 і
три точкові заряди над нею. Вирішити цю
нову задачу достатньо складно, тому що
на поверхні провідника є поляризаційні
заряди, розподіл яких необхідно знати.
Між тим задача спрощується, якщо видалити
провідник і в потрібних точках розташувати
три заряди, так аби на поверхні металу
після заміни була розташована
еквіпотенціальна поверхня. У
методі дзеркальних відображень, замість
вирішення задачі про розподіл потенціалу
в системі заряджених провідників і
зарядів над ними, намагаються підібрати
таке розташування точкових зарядів і
таку їх величину, щоб еквіпотенціальні
поверхні співпадали з поверхнею
провідників і мали потрібне значення
потенціалів.
Умови для векторів напруженості магнітного поля і магнітної індукції на межі двох магнетиків.
Р озглянемо
пласку межу поділу двох магнетиків з
магнітними проникностями
озглянемо
пласку межу поділу двох магнетиків з
магнітними проникностями![]() 1
і
1
і ![]() 2.
Нехай зовнішнє магнітне поле направлене
під кутом до нормалі, межі поділу.
Розкладемо вектори
2.
Нехай зовнішнє магнітне поле направлене
під кутом до нормалі, межі поділу.
Розкладемо вектори ![]() і
і ![]() на
нормальні (
на
нормальні (![]() і
і
![]() )
та тангенціальні (
)
та тангенціальні (![]() і
і
![]() )
складові, аналогічно
)
складові, аналогічно ![]() і
і
![]() .
На межі поділу побудуємо прямокутний
циліндр, висота якого h,
паралельна нормалі. Застосуємо
рівняння:
.
На межі поділу побудуємо прямокутний
циліндр, висота якого h,
паралельна нормалі. Застосуємо
рівняння:![]() .
Тоді:
.
Тоді: ![]() ,
де (-) з’явився тому, що нормалі направлені
протилежно,
,
де (-) з’явився тому, що нормалі направлені
протилежно, ![]() —
потік вектору
—
потік вектору ![]() через бічну
поверхню циліндра. Тепер спрямуємо
висоту циліндра h до
нуля. При цьому значення
через бічну
поверхню циліндра. Тепер спрямуємо
висоту циліндра h до
нуля. При цьому значення ![]() і
і
![]() будуть
знаходитися на самій межі поділу, а
будуть
знаходитися на самій межі поділу, а ![]() . В результаті
. В результаті ![]() —
нормальні складові вектору
—
нормальні складові вектору ![]() на
межі поділу двох магнетиків
неперервні.Оскільки
на
межі поділу двох магнетиків
неперервні.Оскільки ![]() ,
то
,
то ![]() —зв’язок
між нормальними складовими вектору
—зв’язок
між нормальними складовими вектору
![]() .
Тепер проведемо на межі поділу замкнений
контур у вигляді прямокутника зі
сторонами l і
h.
Застосуємо закон повного струму:
.
Тепер проведемо на межі поділу замкнений
контур у вигляді прямокутника зі
сторонами l і
h.
Застосуємо закон повного струму: ![]() , де I —
струм провідності, що відсутній на межі
поділу. З рівняння
, де I —
струм провідності, що відсутній на межі
поділу. З рівняння ![]() , випливає:
, випливає:
![]()
де ![]() —
значення інтеграла на ділянках h
Спрямуємо
—
значення інтеграла на ділянках h
Спрямуємо
![]() . Тоді
. Тоді ![]() і
і ![]() ,
а
,
а ![]() . З одержаних співвідношень випливає
закон заломлення силових ліній векторів
. З одержаних співвідношень випливає
закон заломлення силових ліній векторів
![]() і
і
![]()
 .
.
Диференціальна форма запису теореми Остроградського-Гаусса.
В випадку нерівномірного розподілу заряду і не симетричної конфігурації заряджених кіл зручно користуватися теоремою гауса в диференційній формі.
Нехай заряд в просторі розміщений не рівномірно const
В загальному випадку =f(x,y,z)
Для отримання . теор. Гаусса в нов. формі скористаємося . теор. Гаусса в інтегр. Та теоремою остроградського-гаусса з курсу матаналізу
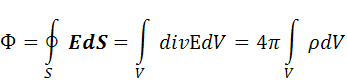
Звідси випливає що
![]() =>
=> ![]()
(Це і є теорем острог.-Гаусса в диф. Формі електростатична)
Аналогічний результат для діалектриків divD=4πρ (де ρ об’ємна густина вільних зарядів)
(
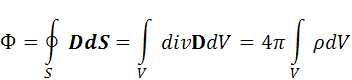
)
Для магнітного поля

divB = 0
