Частотна залежність сумарної діелектричної проникності діелектриків

Частотна залежність сумарної проникності має вигляд, зображений на малюнку. На малих частотах зміни зовнішнього поля молекули встигають орієнтуватись за полем, тому наявні всі три механізми поляризації. При подальшому зростанні частоти зникає йонний механізм поляризації. Згодом при дуже високих частотах зникає і електронний механізм поляризації. Така характеристика справедлива для полярних молекул. В області світлових хвиль (частоти 10¹⁴-10¹⁶ Гц) майже у всіх речовин проникність рівна одиниці. Якщо ж молекули неполярні, то проникність не залежить від частоти.

Закон Ампера для магнітної взаємодії струмів в інтегральній і диференціальній формі.

Закон Ампера є суто експериментальним. Він виражає силу, яка діє на провідник, зі струмом з боку зовнішнього магнітного поля

-Інтегральна форма закону

-диференціальний запис.

Ампер ввів поняття про елемент струму: на провіднику зі струмом  вибирається ділянка ,  — елемент струму, величина векторна, тому що  є вектором.

Закон взаємодії двох елементів струму  і , які знаходяться на відстані , можна в першому наближенні записати: , тобто цей закон подібний до закону Кулона із заміною величини точкових зарядів на елементи струму.

Повний запис закону Ампера має вигляд:

Тут  — сила, яка діє на елемент  з боку елементу

—константа, яка залежить від розмірності величин, що входять у формулу.

Закон Ампера для провідника в полі:

Величину назвемо вектором магнітної індукції.

Можна ввести кут  між і , тоді величина вектору може бути визначена:

Напрямок вектору визначається правилом правого гвинта.

Для вектору справедливий принцип суперпозиції .

Для замкненого струму .

Тоді сила, діюча на деякий елемент струму , що міститься в точці поля, в якій замкнений струм створює вектор , буде

Інтегральна форма

Закон Ампера для магнітної взаємодії струмів в інтегральній і диференціальній формі.

Закон Ампера є суто експериментальним. Він виражає силу, яка діє на провідник, зі струмом з боку зовнішнього магнітного поля

-Інтегральна форма закону

-диференціальний запис.

Ампер ввів поняття про елемент струму: на провіднику зі струмом  вибирається ділянка ,  — елемент струму, величина векторна, тому що  є вектором.

Закон взаємодії двох елементів струму  і , які знаходяться на відстані , можна в першому наближенні записати: 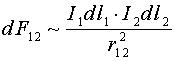, тобто цей закон подібний до закону Кулона із заміною величини точкових зарядів на елементи струму.

Повний запис закону Ампера має вигляд:

Тут  — сила, яка діє на елемент  з боку елементу

—константа, яка залежить від розмірності величин, що входять у формулу.

Закон Ампера для провідника в полі:

Величину назвемо вектором магнітної індукції.

Можна ввести кут  між і , тоді величина вектору може бути визначена:

Напрямок вектору визначається правилом правого гвинта.

Для вектору справедливий принцип суперпозиції .

Для замкненого струму .

Тоді сила, діюча на деякий елемент струму , що міститься в точці поля, в якій замкнений струм створює вектор , буде

Інтегральна форма

Закон трьох других

Закон трьох других виражає залежність сили струму термоелектронної емісії від прикладеної різниці потенціалів. Нехай маємо систему з двох електродів

Запишемо для неї рівняння Пуассона:

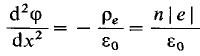n-концентртація електронів;

Запишемо також закон збереження енергії:

, тут v_d- дрейфова швидкість електронів.

Знаючи вираз для об’ємної густини струму можемо записати

Тепер перше рівняння можна переписати у вигляді:

де Домножимо рівняння на і врахувавши, що отримаємо рівняння:

Двічі проінтегрувавши спочатку від 0 до x, одержимо рівняння:

Тепер інтегруємо від 0 до d,врахувавши, що

Остаточно одержимо: