Закон Джоуля-Ленца в класичній електронній теорії металів Друде-Лоренца.

Швидкість руху електрона у провіднику : V=U+V_б, де U-швидкість дрейфу, V_б-швидкість безладного теплового руху.

Над електроном щосеундно виконується робота:

VF=(V_б+U)F

При сумуванні по всіх електронах V_бF дасть нуль. Отже, робота, яка виконується над електронами одиниці об’єму металу A==.В металах ця робота йде на приріствнутрішньої(теплової) енергії, оскільки проходження електричного струму не супроводжуеється змінами внутрішньої структури метала. Таким чином, потужність тепла, що виділяється струмом в одиниці об'єму провідника, має вигляд або, деj=neU (або )-електричний заряд, що переноситься через одиницю площі за одиницю часу; - коефіцієнт електропровідності;- час за який швидкість дрейфового руху(U) у відсутності зовнішніх регулярних сил затухає в е разів. Якщо сила, що діє на електрони в металах чисто електрична, то .

Еквівалентність виразів для електростатичного поля для випадків її локалізації у місці знаходження розподіленого заряду та наявності електростатичного поля.

Для доведеня еквівалентності скористаємося виразом для енергії електростатичного поля у випадку розподіленого заряду:

де -потенціал в точці елемента просторуdv, а - густина заряду.

Скористаємося виразом : , запишемо (1) у вигляді:

З векторного аналізу :

.

Виразимо звідси =.

Тоді представимо (2) у вигляді :

Враховуючи , що : :

.

За теоремою Гауса-Остроградського

.Якщо :

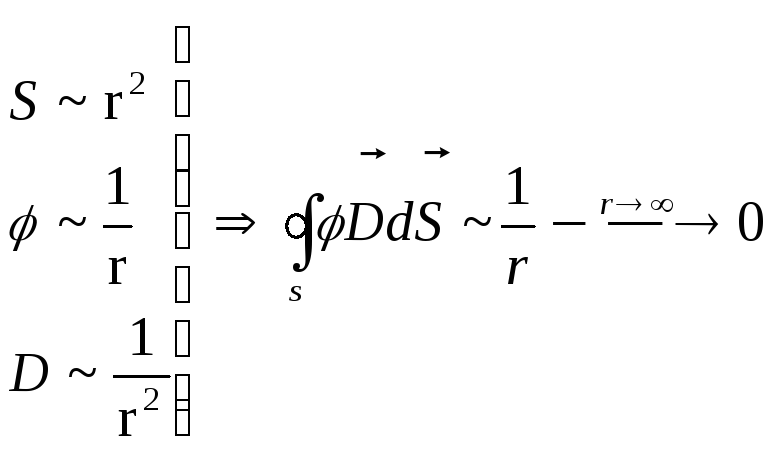. Тобто , остаточно вираз для енергії набуває вигляду: (3). Отже , цим доведене еквівалентність двох виразів для енергії електростатичного поля в залежності від її локалізації:

– енергія локалізована на зарядах , які є носіями енергії;

- енергія локалізована у всьому просторі, в якому присутнє поле, що виступає носієм енергії.

Вектор-потенціал магнітного поля

Вектор-потенціал магнітного поля позначається . Зв’язок векторів  і  задається співвідношенням . Така форма зв’язку дозволяє задовольнити одне з рівнянь Максвелла: . Подібно до скалярного потенціалу  в електростатиці, вектор-потенціал задається неоднозначно, однак, свобода вибору тут більш широка. Нехай є вектор , якому відповідає вектор . Розглянемо тепер вектор , де  — будь-яка функція, для якої визначено градієнт. Знайдемо , тому що . Таким чином,  і  дають одне і те ж значення магнітної індукції. Цією свободою вибору можна скористатися для того, щоб накласти на вектор  додаткову умову:  (тобто поле вектору  соленоїдальне).Скористаємося тепер другим рівнянням Максвелла для магнетостатики:, , Але . Ми прийшли до рівняння яке є рівнянням Пуассона, але для векторних функцій. Це рівняння можна замінити трьома скалярними: , , Розв’язками цих рівнянь будуть:

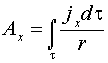
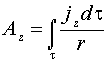
або у векторній формі:

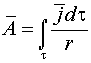
Таким чином, знаючи розподіл густини струму у просторі, можна знайти вектор , а відтак, і вектор магнітної індукції Вектор  має ще одну властивість. Нехай у магнітному полі вибрано деякий контур і натягнуто на нього довільну поверхню . Потік вектору  через цю поверхню:

тут ми скористалися формулою Стокса. Таким чином,  — потік вектору   через поверхню, натягнуту на контур, дорівнює циркуляції вектору  по цьому контуру. Це аналог закону повного струму , де роль потоку  грає  ( – також потік, але вектору ), роль вектору  грає вектор