- •«Динамика»
- •2403.309003.000Пз
- •Контрольная работа д1 Динамика материальной точки
- •Контрольная работа д2 Колебания материальной точки
- •Контрольная работа д3 Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела
- •Контрольная работа д4 Применение теоремы об изменении кинетической энергии к изучению движения механической системы
- •Контрольная работа д5 Применение общего уравнения динамики к изучению движения механической системы с одной степенью свободы
- •Контрольная работа д6 Применение уравнений Лагранжа второго рода к изучению движения механической системы с двумя степенями свободы
Контрольная работа д4 Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Механическая система, изображенная на рис.1, приводится в движение из состояния покоя. При этом колесо В катится без скольжения по плоскости.
Массы
тел:
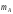 =300
кг,
=300
кг,
 =100
кг,
=100
кг, =10
кг
=10
кг
Заданная нагрузка: М=20 Н∙м и F=500 Н
Радиусы колеса В и шкива D соответственно равны RВ=0,8 м, rВ=0,5 м, RD=0,2м, радиус инерции колеса В ρВ=0,3 м
Углы имеют следующие значения: α=300, β=600
Коэффициент трения качения равен k = 0,05∙RВ; коэффициент трения скольжения тела А равен f = 0,1.
Используя теорему об изменении кинетической энергии системы, определить скорость и ускорение тела А после того, как оно переместится на расстояние SА=2м. Шкив D считать однородным сплошным диском; силами сопротивления в подшипниках, массой троса, его растяжением и проскальзыванием по ободу шкива пренебречь.
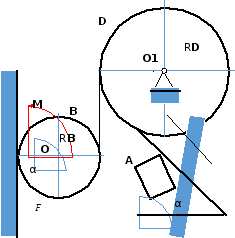
Рис.1
РЕШЕНИЕ:

Для определения скорости и ускорения груза А воспользуемся теоремой об изменении кинетической энергии:
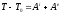 . (1)
. (1)
Где
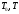 - кинетическая энергия системы в начальном
и конечном положениях
- кинетическая энергия системы в начальном
и конечном положениях
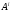 -
суммарная работа внутренних сил,
действующих на систему, при ее переходе
из начального положения в конечное.
-
суммарная работа внутренних сил,
действующих на систему, при ее переходе
из начального положения в конечное.
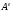 -
суммарная работа внешних сил, действующих
на систему, при ее переходе из начального
положения в конечное.
-
суммарная работа внешних сил, действующих
на систему, при ее переходе из начального
положения в конечное.
Определяем
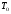 и
и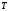 .
Так как в начальный момент система
находится в покое, то
.
Так как в начальный момент система
находится в покое, то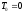 .
Величина
.
Величина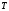 равна сумме кинетических энергий всех
тел системы:
равна сумме кинетических энергий всех
тел системы:
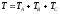 .
.
Учитываем:
1)
груз А движется поступательно со
скоростью
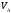 ,
следовательно
,
следовательно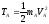
2)
Шкив D вращается вокруг неподвижной оси
с угловой скоростью
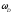 ,
следовательно
,
следовательно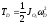 ;
;
Так
как шкив D считаем однородным цилиндром,
то его момент инерции относительно оси,
проходящей через точку О1:
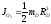 ,
то есть
,
то есть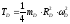 ;
;
3)
Колесо В, движется плоскопараллельно:
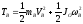 ,
где
,
где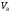 - скорость центра масс блока В,
- скорость центра масс блока В,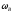 - угловая скорость колеса В.
- угловая скорость колеса В.
Момент
инерции колеса В относительно оси,
проходящей через точку О:
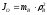 .
.
Так
как колесо В катится по плоскости без
проскальзывания, то скорость точки Р
(рис.2) колеса В равняется нулю и она
является мгновенным центром скоростей
этого тела. Тогда угловая скорость
колеса В:
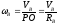 .
Следовательно,
.
Следовательно,
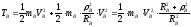 .
.
Тогда
кинетическая энергия механической
системы:
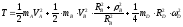 (2)
(2)
Выразим
все скорости через
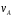 .
Так как нити нерастяжимы, то скорость
точки I диска D равна скорости центра
масс груза А
.
Так как нити нерастяжимы, то скорость
точки I диска D равна скорости центра
масс груза А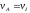 ,
но
,
но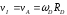
Следовательно,
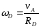 . (3)
. (3)
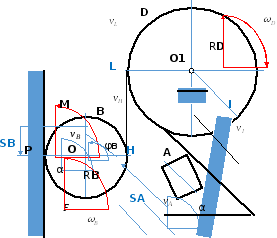
Рис.2
Скорость
точки L диска D равна скорости точки Н
колеса В
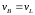 .
Так как точка Р – мгновенный центр
скоростей колеса В, то
.
Так как точка Р – мгновенный центр
скоростей колеса В, то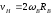 .
Учитывая, что
.
Учитывая, что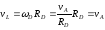 ,
получим:
,
получим:
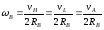
и
так как
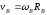 ,
то
,
то
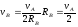 (4)
(4)
Тогда
, подставив (3) и (4) в (2), получим:
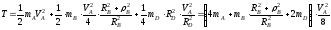 (5)
(5)
Так
как тела, образующие систему, абсолютно
твердые и трос – нерастяжимый, то
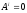 (6).
(6).
На
систему действуют внешние силы (рис.3):
силы тяжести
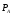 ,
,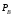 ,
,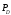 ,
реакции
,
реакции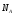 ,
,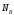 ,
,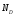 ,
сила трения скольжения
,
сила трения скольжения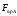 ,
действующая на груз А, сила трения
,
действующая на груз А, сила трения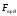 ,
действующая на колесо В и момент
,
действующая на колесо В и момент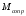 сил сопротивления качению блока В, а
так же приложенные к колесу В сила
сил сопротивления качению блока В, а
так же приложенные к колесу В сила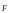 и момент пары сил М.
и момент пары сил М.
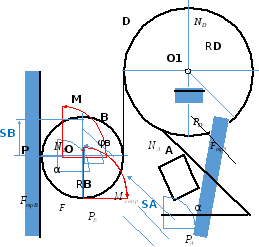
Рис. 1
Найдем
сумму работ всех действующих внешних
сил при перемещении, которое будет иметь
система, когда груз А пройдет путь
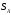 .
Обозначим:
.
Обозначим: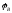 - угол поворота колеса В,
- угол поворота колеса В,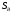 - перемещение центра масс колеса В.
- перемещение центра масс колеса В.
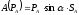 ,
,
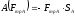 ,
,
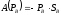 ,
,
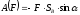 ,
,
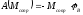 ,
,
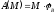
Работы
остальных сил равны нулю, так точка
приложения
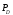 и
и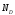 неподвижна,
неподвижна,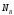 перпендикулярна перемещению колеса В,
перпендикулярна перемещению колеса В,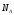 перпендикулярна перемещению груза А,
точка Р, где приложена сила
перпендикулярна перемещению груза А,
точка Р, где приложена сила – мгновенный центр скоростей колеса
В.
– мгновенный центр скоростей колеса
В.
Выразим
угол поворота колеса В и перемещение
центра масс блока В через перемещение
груза А
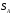 ,
учитывая что зависимость между
перемещениями такая же как и между
скоростями:
,
учитывая что зависимость между
перемещениями такая же как и между
скоростями:
Так
как
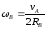 и
и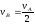 ,
то
,
то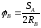 и
и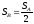
Учитывая,
что сила трения скольжения определяется
выражением:
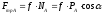 ,
,
и момент сопротивления качению:
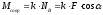
Силы тяжести тел системы:

Следовательно, работы внешних сил равны:
 ,
,
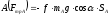 ,
,
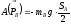 ,
,
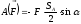 ,
,
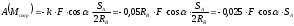 ,
,
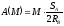

Сумма вычисленных работ равна
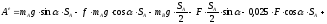
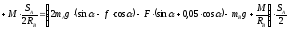 (7)
(7)
Подставляя
выражения (5),(6) и (7) в (1) получаем уравнение
для искомой величины
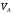 :
:
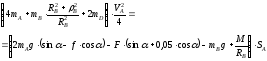 (8)
(8)
Откуда получаем:
 (9)
(9)
Продифференцируем обе части уравнения (8) по времени:
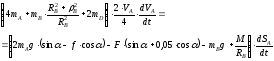
Так
как
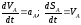 ,
то
,
то

Или
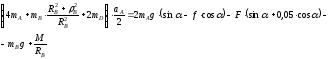
Тогда ускорение груза А:
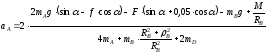 (10)
(10)
Подставляя исходные данные, получим:
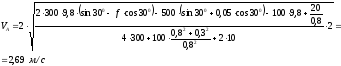
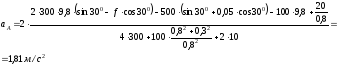
Ответ:
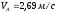 ;
;