- •«Динамика»
- •2403.309003.000Пз
- •Контрольная работа д1 Динамика материальной точки
- •Контрольная работа д2 Колебания материальной точки
- •Контрольная работа д3 Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела
- •Контрольная работа д4 Применение теоремы об изменении кинетической энергии к изучению движения механической системы
- •Контрольная работа д5 Применение общего уравнения динамики к изучению движения механической системы с одной степенью свободы
- •Контрольная работа д6 Применение уравнений Лагранжа второго рода к изучению движения механической системы с двумя степенями свободы
Контрольная работа д3 Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела
Тело
D массой m1
вращается вокруг вертикальной оси Оz
с угловой скоростью ω0
(рис.
1). При этом в точке М желоба АВ тела D на
расстоянии АМ от точки А, отсчитываемом
вдоль желоба, закреплена материальная
точка К массой m2.
В момент времени t
=
0 на систему начинает действовать пара
сил с моментом
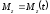 .
Приt
=
t1
действие пары сил прекращается,
одновременно точка К начинает относительное
движение по жёлобу согласно закону
.
Приt
=
t1
действие пары сил прекращается,
одновременно точка К начинает относительное
движение по жёлобу согласно закону
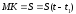 .
Определить
угловые скорости тела D в моменты времени
t
=
t1
и
t =
t2.
.
Определить
угловые скорости тела D в моменты времени
t
=
t1
и
t =
t2.
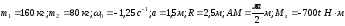
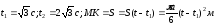
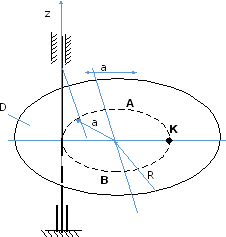
Рис.1
Решение
Рассмотрим механическую систему, состоящую из тела D и материальной точки К. Для определения угловых скоростей тела D применим теорему об
изменении
кинетического момента системы относительно
оси z:

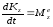 (1)
(1)
где
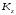 - кинетический момент системы относительно
оси z,
- кинетический момент системы относительно
оси z,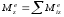 - главный момент внешних сил, приложенных
к системе относительно оси z.
- главный момент внешних сил, приложенных
к системе относительно оси z.
Рассмотрим
движение системы на отрезке времени
от t
=
0 до
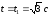 .
.
На
систему действуют внешние силы (рис.2)
: силы тяжести тела D и материальной
точки К
 и
и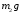 ,
реакции опор вала
,
реакции опор вала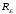 ,
,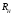 и момент
и момент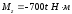 .
Т.к. силы
.
Т.к. силы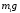 и
и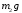 параллельны осиz,
а
реакции
параллельны осиz,
а
реакции
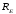 и
и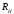 пересекают
ее, то их моменты относительно этой оси
равны нулю. Тогда
пересекают
ее, то их моменты относительно этой оси
равны нулю. Тогда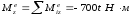 (2)
(2)
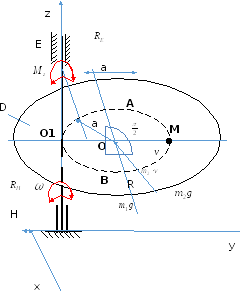

Рис.2
Для
рассматриваемой механической системы 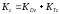 ,
где
,
где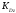 и
и – кинетические моменты относительно
оси z тела D и материальной точки К,
соответственно.
– кинетические моменты относительно
оси z тела D и материальной точки К,
соответственно.
Тело
D вращается вокруг неподвижной оси
z, следовательно
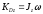 .
.
Момент
инерции тела относительно оси
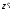 ,
параллельной оси z и проходящей через
центр масс О тела:
,
параллельной оси z и проходящей через
центр масс О тела: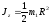
По
теореме Штейнера
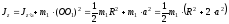 .
.
Следовательно
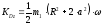 .
.
Кинетический момент материальной точки К, закрепленной в точке М:
 .
.
Так как точка К совершает вращательное движение вместе с телом D, то
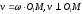
По
условию задачи
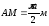 ,тогда
центральный угол АОМ, на который опирается
дуга АМ:
,тогда
центральный угол АОМ, на который опирается
дуга АМ:
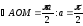
Тогда
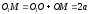
И кинетический момент материальной точки К, закрепленной в точке М:
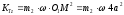
Тогда кинетический момент системы:
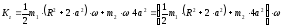 (3)
(3)
Подставив (3) и (2) в (1), получим:
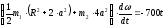
Или, учитывая начальные данные:
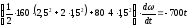

Разделяем в последнем уравнении переменные и интегрируем правую и левую части:
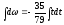
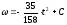
Так
как в начальный момент времени
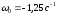 ,
то
,
то
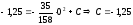
И
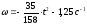 уравнение
угловой скорости тела D на отрезке
времени от t = 0 до
уравнение
угловой скорости тела D на отрезке
времени от t = 0 до
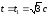
При
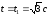
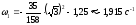
Рассмотрим
теперь движение системы на отрезке
времени от
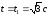 до
до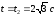 .
.
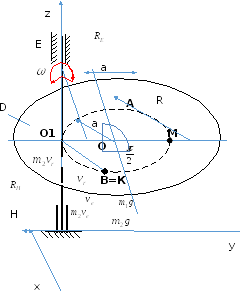

Рис.3
На
систему действуют те же внешние силы
(рис.3), за исключением момента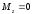 .
Тогда
.
Тогда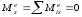 (4)
(4)
Тогда
уравнение (1) можно записать в виде:
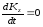 ,
то есть
,
то есть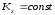 .
.
В
момент времени
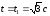 кинетический момент системы:
кинетический момент системы:
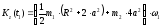 (5)
(5)
В
момент времени
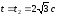 материальная точка находится в точке
В, так как длина дуги МК:
материальная точка находится в точке
В, так как длина дуги МК:
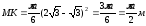 и
центральный угол МОК, на который опирается
дуга МК:
и
центральный угол МОК, на который опирается
дуга МК:
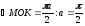
В
момент времени
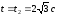 кинетический момент тела D:
кинетический момент тела D:
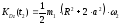
Для
определения кинетического момента
материальной точки К рассмотрим движение
точки К как сложное, считая ее движение
по желобу относительным, а вращение
самого тела D – переносным движением.
Тогда
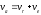 .
.
Следовательно,
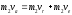
И
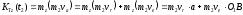
Так
как
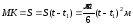 ,
то
,
то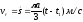 .
.
При
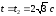
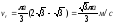
Переносная
скорость
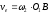
Из прямоугольного треугольника О1ОВ получим:
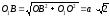
И
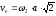
Тогда
кинетический момент материальной точки
К при
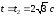 :
:
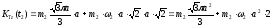
И
кинетический момент системы при
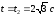 :
:
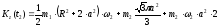 (6).
(6).
Так
как
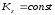 ,
то приравнивая (5) и (6), получим:
,
то приравнивая (5) и (6), получим:
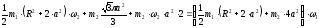
или
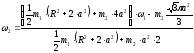
Откуда находим: