МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«Уфимский государственный авиационный технический университет»

ФИЛИАЛ В ГОРОДЕ СТЕРЛИТАМАКЕ

КАФЕДРА ЕСТЕСТВЕННО-НАУЧНЫХ И ОБЩЕПРОФЕССИОНАЛЬНЫХ ДИСЦИПЛИН

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

по дисциплине «Теоретическая механика»

«Динамика»

2403.309003.000Пз

(обозначение документа)

Группа КТОС-105сф	Фамилия И.О.	Подпись	Дата	Оценка
Студент	Моргунов М.В.
Проверил	Салихов Р.Ф.

Стерлитамак 2016 г.

Содержание

Контрольная работа Д1 4

Контрольная работа Д2 9

Контрольная работа Д3 14

Контрольная работа Д4 20

Контрольная работа Д5 27

Контрольная работа Д6 33

Литература 39

Контрольная работа д1 Динамика материальной точки

Груз D массой m=5кг, получив в точке А начальную скорость V₀=2м/с, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости. На участке АВ на груз кроме силы тяжести 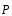действует сила сопротивления среды 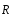, зависящая от скорости 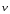груза,R=0,1V².

В точке В груз, изменив направление приобретенной скорости, но сохранив при этом ее величину, переходит на участок ВС трубы, где на него кроме силы тяжести действует сила трения (коэффициент трения груза о трубу f = 0,2) и переменная по величине сила 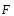, направленная вдоль участка ВС, проекция которой на осьВх: F_x =0,5cos²(πt).

Считая груз материальной точкой и зная расстояние АВ=l=3м движения груза от точки А до точки В, найти уравнение х=х(t) движения груза на участке ВС.

α=90⁰

Рис.1

Решение:

Считаем груз материальной точкой.

Рассмотрим движение груза D на участке АВ трубы. Изображаем груз (в произвольном положении) и действующие на него силы ,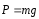(рис.1).

Проводим ось Ах₁ и составляем дифференциальное уравнение в проекции на эту ось:

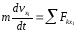
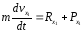
Учитывая, что 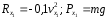, получим :

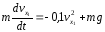
Учитывая, что

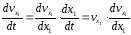
Запишем уравнение в виде :

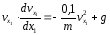
Учитывая исходные данные и считая 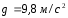, получим:

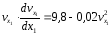
Разделяем переменные и интегрируем уравнение :

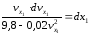
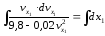
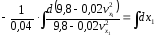
или

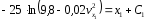
Для нахождения постоянной интегрирования С₁ используем начальные условия: 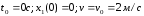. Получим:

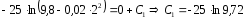
Тогда

Преобразуем уравнение

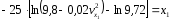
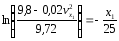
Потенциируем:

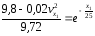
Окончательно получаем:

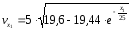
Найдем скорость тела в точке В, при АВ=l=3м:

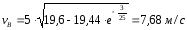
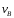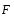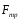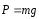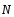Рассмотрим движение груза на участке ВС, найденная скорость будет для движения на этом участке начальной скоростью. Изображаем действующие на груз силы ,,, реакцию трубы_. Проведем из точки В оси Вx и Ву (рис.1) и дифференциальные уравнения движения груза в проекциях на оси координат примут вид:

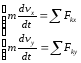
Так как тело движется вдоль оси х, то :

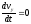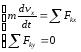
Из второго уравнения системы получаем:

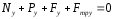
Или

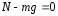
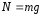
Тогда

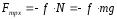
Учитывая, что 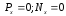; 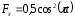из первого уравнения получим:

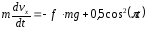
Или

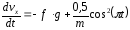
Учитывая исходные данные, получим:

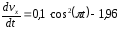
Для упрощения дальнейших вычислений используем формулу косинуса двойного угла:

:

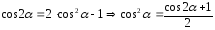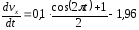
Или

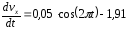
Разделяем переменные и интегрируем:

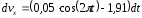
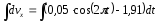
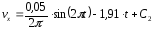
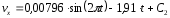
Для нахождения С₂ используем начальные условия:

t=t₀=0, v_x(0)=.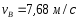

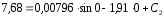, следовательно,

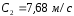
Тогда,

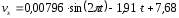
Так как 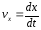, то получим дифференциальное уравнение для нахождения закона движения груза на участке ВС:

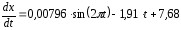
Разделяем переменные и интегрируем:

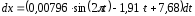
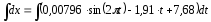
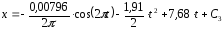
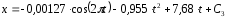
Так как t=t₀=0, x=x₀=0, то

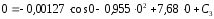
и окончательно искомый закон движения груза будет иметь вид:

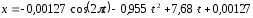, где х – в метрах, t – в секундах.