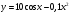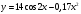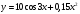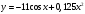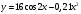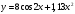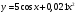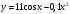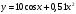Для БПМ13 / Численные методы лаб / 2.Решение нелинейных уравнений
.docxЗадание
-
найти корень уравнения y=f(x) с заданной точностью методом Ньютона, секущих, хорд и комбинированным методом, используя функции MathCAD;
-
исследовать обусловленность методов и зависимость числа итераций от точности числа eps, при изменении Eps от 0,1 до 0,000001;
-
графически и аналитически отделить корень уравнения - найти отрезки на которых функция удовлетворяет условиям применимости методов;
-
выполнить вычисления по программе MathCAD;
-
теоретически и экспериментально сравнить методы по скорости сходности и степени обусловленности;
-
результаты оформить в виде отчета, содержащего постановку задачи, тексты программ;
-
результаты теоретического и экспериментального анализа в виде таблиц и графиков;
-
выводы.
|
Вар. |
y=f(x) |
Вар. |
y=f(x) |
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
Решение нелинейных уравнений
Метод Ньютона (метод касательных)
Пусть
корень
 уравнения
уравнения
 отделен на отрезке
отделен на отрезке
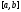 .
Предположим мы нашли
.
Предположим мы нашли
 -ое
приближение корня
-ое
приближение корня
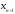 .
Тогда
.
Тогда
 -ое
приближение
-ое
приближение
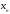 мы можем получить следующим образом.
Положим
мы можем получить следующим образом.
Положим
 .
(1)
.
(1)
Раскладывая
в ряд
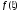 в точке
в точке
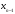 ,
получим
,
получим
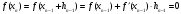 .
.
Отсюда следует
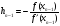 .
(2)
.
(2)
Подставим (2) в формулу (1), получим
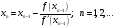 (3)
(3)
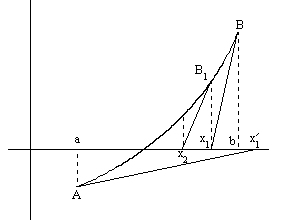
Рисунок 1 - Геометрическая интерпретация метода Ньютона
Геометрически
метод Ньютона эквивалентен замене дуги
кривой
 касательной, проведенной в некоторой
точке кривой (см. рис.1).
касательной, проведенной в некоторой
точке кривой (см. рис.1).
В
точке
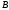 имеем
имеем
 .
Здесь
.
Здесь
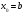 .
Проведем касательную в точке
.
Проведем касательную в точке
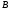 ,
получим на пересечении касательной
осью
,
получим на пересечении касательной
осью
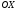 точку
точку
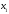 .
Далее проводим касательную в точке
.
Далее проводим касательную в точке
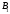 ,
получим точку
,
получим точку
 и т.д.
и т.д.
Если
положить
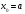 ,
то в точке
,
то в точке
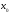 будем иметь
будем иметь
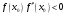 .
Тогда касательная в точке
.
Тогда касательная в точке
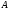 пересекла бы ось
пересекла бы ось
 в точке
в точке
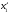 ,
лежащей вне отрезка
,
лежащей вне отрезка
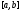 ,
то есть при таком выборе начальной
точки, метод Ньютона оказывается
расходящимся. Достаточные условия
сходимости метода Ньютона определяются
следующей теоремой.
,
то есть при таком выборе начальной
точки, метод Ньютона оказывается
расходящимся. Достаточные условия
сходимости метода Ньютона определяются
следующей теоремой.
Теорема.
Если
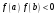 ,
причем
,
причем
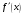 и
и
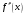 отличны от нуля и сохраняют определенные
знаки при
отличны от нуля и сохраняют определенные
знаки при
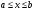 ,
то исходя из начального приближения
,
то исходя из начального приближения
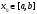 ,
удовлетворяющего неравенству
,
удовлетворяющего неравенству
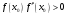 можно вычислить методом Ньютона
единственный корень
можно вычислить методом Ньютона
единственный корень
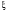 уравнения
уравнения
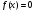 с любой степенью точности.
с любой степенью точности.
Критерий завершения итерационного процесса имеет вид
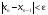 .
.
Метод секущих
Если
итерации
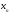 и
и
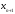 расположены достаточно близко друг к
другу, то производную
расположены достаточно близко друг к
другу, то производную
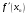 в алгоритме Ньютона можно заменить ее
приближенным значением
в алгоритме Ньютона можно заменить ее
приближенным значением
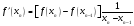 .
.
Таким образом, из формулы метода Ньютона получим формулу секущих
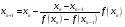 .
.
Геометрический
смысл такого изменения алгоритма Ньютона
состоит в том, что от аппроксимации
 касательной мы переходим к секущей (см.
рис.2).
касательной мы переходим к секущей (см.
рис.2).
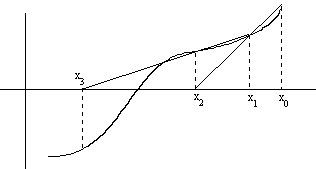
Рисунок
2 - Здесь задаются в начале итерационного
процесса две точки
 и
и
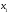 .
.
Останов:
 где
где
 - заданная точность.
- заданная точность.
Метод
секущих уступает методу Ньютона в
скорости сходимости, однако не требует
вычисления производной функции
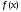 .
.
Метод хорд
Рассмотрим
более быстрый способ нахождения корня
на интервале [a,b],
в предположении, что
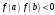 .
.
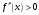
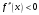
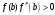
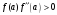
Рис.3(а) Рис. 3(б)
Рассмотрим рис.3а. Проведем через точки А и В хорду. Уравнение хорды
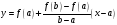 .
.
В
точке
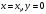 ,
в результате получим первое приближение
корня
,
в результате получим первое приближение
корня
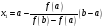 .
(4)
.
(4)
Проверяем условия
(а)
 ,
,
(б)
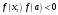 .
.
Если
выполняется условие (а), то в формуле
(4) точку
 заменяем на
заменяем на
 ,
получим
,
получим
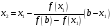 .
.
Продолжая этот процесс, получим для n-го приближения
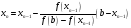 .
(5)
.
(5)
Здесь
подвижен конец
 ,
то есть
,
то есть
 .
Аналогичная ситуация на рис 3а.
.
Аналогичная ситуация на рис 3а.
Рассмотрим
случай, когда неподвижен конец
 .
.
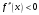
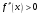
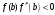
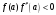
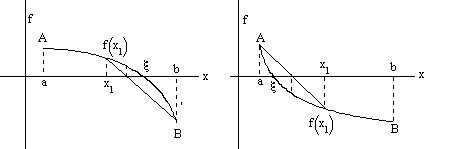
Рисунок 4(а) Рисунок 4(б)
На
рис 4а,4б выполняется
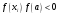 .
Записав уравнение хорды, мы на первом
шаге итерационного процесса получим
.
Записав уравнение хорды, мы на первом
шаге итерационного процесса получим
 . Здесь выполняется
. Здесь выполняется
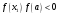 .
Затем вводим
.
Затем вводим
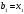 , точку
, точку
 заменяем на
заменяем на
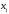 ),
получим
),
получим
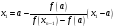 .
.
Продолжая процесс, придем к формуле
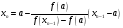 .
.
Останов процесса
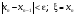
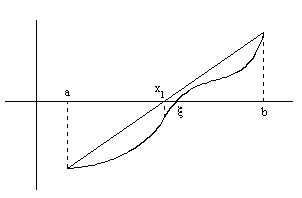
Рисунок 5
На
рис. 5
 меняет знак, поэтому подвижными будут
оба конца.
меняет знак, поэтому подвижными будут
оба конца.
Теорема.
Пусть задана непрерывная: дважды
дифференцируемая функция
 на
на
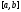 и пусть
и пусть
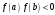 ,
а
,
а
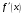 и
и
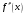 сохраняют свои знаки на
сохраняют свои знаки на
 .
Тогда итерационный процесс метода хорд
сходится к корню
.
Тогда итерационный процесс метода хорд
сходится к корню
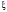 с любой наперед заданной точностью
с любой наперед заданной точностью
 .
.
Комбинированный метод
Пусть
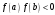 ,
а
,
а
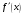 и
и
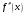 сохраняют знаки на
сохраняют знаки на
 .
Объединяя метод хорд и метод Ньютона,
можно ускорить сходимость итерационного
процесса поиска корня. В результате мы
получаем комбинированный метод, на
каждом шаге которого находим значение
обоих границ интервалов, внутри которых
содержится корень. Также как и в методе
хорд, рассмотрим следующие ситуации
.
Объединяя метод хорд и метод Ньютона,
можно ускорить сходимость итерационного
процесса поиска корня. В результате мы
получаем комбинированный метод, на
каждом шаге которого находим значение
обоих границ интервалов, внутри которых
содержится корень. Также как и в методе
хорд, рассмотрим следующие ситуации
Если
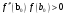 (то есть
(то есть
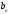 - неподвижен, рис.4) то
- неподвижен, рис.4) то
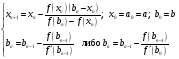 (6)
(6)
Здесь
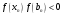
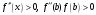
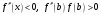
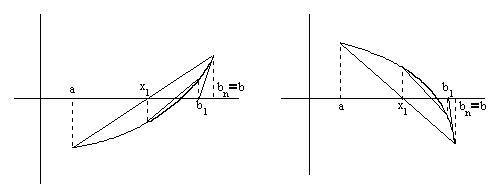 Рисунок
6(а) Рисунок
6(б)
Рисунок
6(а) Рисунок
6(б)
2)
Если
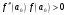 (
(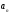 - неподвижен, см.рис. 6), то
- неподвижен, см.рис. 6), то
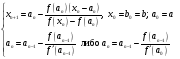 (7)
(7)
Здесь
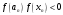 .
.
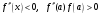
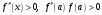
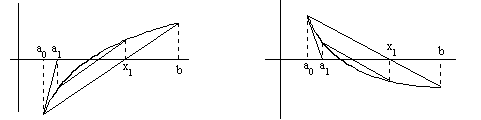
Рисунок 7(а) Рисунок 7(б)