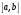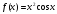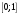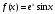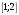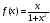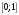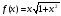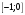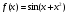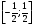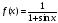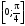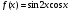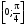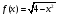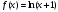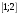Для БПМ13 / Численные методы лаб / 4.Численное дифференцирование
.docxЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
-
Некорректность операции численного дифференцирования
Задача
численного дифференцирования состоит
в приближенном вычислении производных
функции
 по заданным в конечном числе точек
значениям этой функции. Разобьем отрезок
по заданным в конечном числе точек
значениям этой функции. Разобьем отрезок
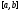 на
на
 одинаковых частей
одинаковых частей
 где
где
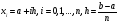 .
Пусть определены значения
.
Пусть определены значения
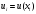 функции
функции
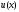 .
В качестве приближенного значения
.
В качестве приближенного значения
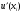 можно взять любое из следующих разностных
отношений
можно взять любое из следующих разностных
отношений
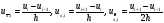 ,
,
называемых, соответственно, левой, правой и центральной разностными производными. Возникающая в результате такой замены погрешность, называемая погрешностью аппроксимации, характеризуется оценками
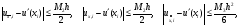
где
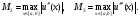 Таким образом, погрешность аппроксимации
Таким образом, погрешность аппроксимации
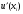 левой и правой разностными производными
является величиной
левой и правой разностными производными
является величиной
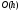 при
при
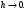 В этом случае говорят, что имеет место
аппроксимация первого порядка. Центральная
разностная производная аппроксимирует
В этом случае говорят, что имеет место
аппроксимация первого порядка. Центральная
разностная производная аппроксимирует
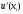 со вторым порядком и, следовательно,
является более точным приближением к
со вторым порядком и, следовательно,
является более точным приближением к
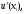 чем левая или правая разностные
производные.
чем левая или правая разностные
производные.
Вторую
производную в точке
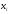 можно заменить второй разностной
производной
можно заменить второй разностной
производной
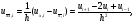 при этом
при этом
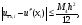 где
где
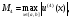 т.е. имеет место аппроксимация второго
порядка.
т.е. имеет место аппроксимация второго
порядка.
Как
правило, значения функции
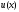 в точках
в точках
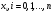 вычисляются не точно, а с каким-то
приближением. Например, элементарные
трансцендентные функции вычисляются
с помощью рядов, причем ряды заменяются
конечными суммами. Другим источником
погрешностей являются погрешности
округления. Оказывается, что погрешность,
возникающая при вычислении разностных
отношений, намного превосходит погрешность
в задании значений функции
вычисляются не точно, а с каким-то
приближением. Например, элементарные
трансцендентные функции вычисляются
с помощью рядов, причем ряды заменяются
конечными суммами. Другим источником
погрешностей являются погрешности
округления. Оказывается, что погрешность,
возникающая при вычислении разностных
отношений, намного превосходит погрешность
в задании значений функции
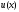 и даже может неограниченно возрастать
при стремлении шага
и даже может неограниченно возрастать
при стремлении шага
 к нулю. Поэтому операцию вычисления
разностных отношений называют
некорректной. Поясним причину
некорректности на примере вычисления
разностного отношения
к нулю. Поэтому операцию вычисления
разностных отношений называют
некорректной. Поясним причину
некорректности на примере вычисления
разностного отношения
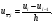
Разностное
отношение
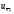 хорошо приближает
хорошо приближает
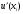 только в том случае, когда шаг
только в том случае, когда шаг
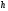 достаточно мал. Требование малости
величины
достаточно мал. Требование малости
величины
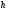 ,
находящейся в знаменателе разностного
отношения, как раз и является причиной
некорректности операции численного
дифференцирования. Действительно, пусть
вместо точного значения
,
находящейся в знаменателе разностного
отношения, как раз и является причиной
некорректности операции численного
дифференцирования. Действительно, пусть
вместо точного значения
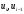 вычислены приближенные значения
вычислены приближенные значения
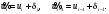 Тогда вместо
Тогда вместо
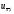 будет вычислена величина
будет вычислена величина
 Следовательно, погрешность в вычислении
первой разностной производной окажется
равной
Следовательно, погрешность в вычислении
первой разностной производной окажется
равной
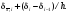 Пусть
Пусть
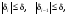 тогда
тогда
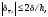 причем эта оценка достигается при
причем эта оценка достигается при
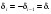 Из этой оценки видно, что вследствие
малости
Из этой оценки видно, что вследствие
малости
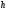 погрешность, возникающая при вычислении
первой разностной производной, значительно
превосходит погрешность вычисления
самой функции
погрешность, возникающая при вычислении
первой разностной производной, значительно
превосходит погрешность вычисления
самой функции
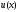 .
Если
.
Если
 не зависит от
не зависит от
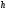 ,
то погрешность
,
то погрешность

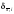 неограниченно возрастает при
неограниченно возрастает при
 Далее погрешность такого рода будем
называть погрешностью округления.
Далее погрешность такого рода будем
называть погрешностью округления.
Сказанное
не означает, что нельзя пользоваться
формулами численного дифференцирования.
Чтобы не происходило существенного
понижения точности, надо следить за
тем, чтобы погрешность округления имела
тот же порядок, что и погрешность
аппроксимации. Например, погрешность
аппроксимации при замене
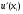 отношением
отношением
 не превосходит величины
не превосходит величины
 где
где
 Естественно потребовать, чтобы и
погрешность округления
Естественно потребовать, чтобы и
погрешность округления
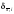 была бы сравнима с погрешностью
аппроксимации, например,
была бы сравнима с погрешностью
аппроксимации, например,
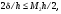 где
где
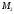 не зависит от
не зависит от
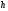 .
Это означает, что погрешность
.
Это означает, что погрешность
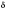 при вычислении значений функции
при вычислении значений функции
 должна быть величиной
должна быть величиной
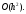 С другой стороны, это неравенство
показывает, что если величина
С другой стороны, это неравенство
показывает, что если величина
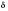 задана, и мы не можем ее менять, то
вычисления надо проводить не с произвольно
малым шагом
задана, и мы не можем ее менять, то
вычисления надо проводить не с произвольно
малым шагом
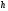 ,
а с шагом, удовлетворяющим условию
,
а с шагом, удовлетворяющим условию
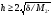 Например, если
Например, если
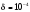 ,
то шаг
,
то шаг
 надо брать примерно равным 0,01. При этом
погрешность аппроксимации и погрешность
округления будут примерно равными
надо брать примерно равным 0,01. При этом
погрешность аппроксимации и погрешность
округления будут примерно равными
 .
.
Вычисление
производной
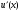 по заданной функции
по заданной функции
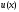 также является некорректной операцией
в том смысле, что для ограниченной
функции
также является некорректной операцией
в том смысле, что для ограниченной
функции
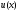 производная
производная
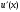 может быть сколь угодно большой. Например,
для
может быть сколь угодно большой. Например,
для
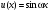 имеем
имеем
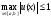 и
и
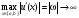 при
при

-
Применение интерполирования
Многие
формулы численного дифференцирования
можно получить как следствие
интерполяционных формул. Для этого
достаточно заменить функцию
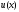 ее интерполяционным многочленом
ее интерполяционным многочленом
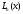 и вычислить производные многочлена
и вычислить производные многочлена
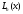 ,
используя его явное представление.
Рассмотрим разбиение отрезка
,
используя его явное представление.
Рассмотрим разбиение отрезка
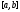 на
на
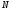 частей:
частей:
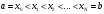 и обозначим через
и обозначим через
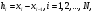 шаги этого разбиения. В качестве примера
получим формулы численного дифференцирования,
основанные на использовании многочлена
Лагранжа
шаги этого разбиения. В качестве примера
получим формулы численного дифференцирования,
основанные на использовании многочлена
Лагранжа
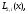 построенного для функции
построенного для функции
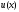 по трем точкам
по трем точкам
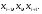 Многочлен
Многочлен
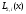 имеет вид
имеет вид
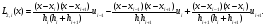
Отсюда получим
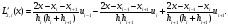
Это
выражение можно принять за приближенное
значение
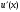 в любой точке
в любой точке
 Его удобнее записать в виде
Его удобнее записать в виде

где
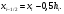 В частности, при
В частности, при
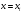 получим
получим
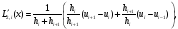
и
если разбиение равномерное,
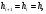 то приходим к центральной разностной
производной,
то приходим к центральной разностной
производной,
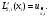 При использовании интерполяционного
многочлена первой степени точно таким
же образом можно получить односторонние
разностные производные
При использовании интерполяционного
многочлена первой степени точно таким
же образом можно получить односторонние
разностные производные
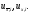 Далее, вычисляя вторую производную
многочлена
Далее, вычисляя вторую производную
многочлена
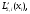 получим приближенное выражение для
получим приближенное выражение для
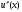 при
при
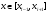
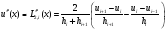
При
равномерном разбиении это выражение
совпадает со второй разностной производной
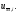 Для приближенного вычисления дальнейших
производных уже недостаточно многочлена
Для приближенного вычисления дальнейших
производных уже недостаточно многочлена
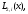 надо привлекать многочлены более
высокого порядка и тем самым увеличивать
число узлов, участвующих в аппроксимации.
Порядок погрешности аппроксимации
зависит как от порядка интерполяционного
многочлена, так и от расположения узлов
интерполяции. Приведем выражение для
погрешности аппроксимации, возникающей
при замене
надо привлекать многочлены более
высокого порядка и тем самым увеличивать
число узлов, участвующих в аппроксимации.
Порядок погрешности аппроксимации
зависит как от порядка интерполяционного
многочлена, так и от расположения узлов
интерполяции. Приведем выражение для
погрешности аппроксимации, возникающей
при замене
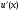 выражением
выражением
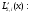

где
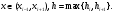
Отсюда
видно, что
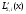 аппроксимирует
аппроксимирует
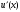 со вторым порядком. Хуже обстоит дело
с аппроксимацией второй производной:
со вторым порядком. Хуже обстоит дело
с аппроксимацией второй производной:
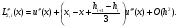
Здесь
даже при равномерном разбиении второй
порядок аппроксимации имеет место лишь
в точке
 а относительно других точек (например,
точек
а относительно других точек (например,
точек
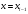 и
и
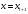 )
выполняется аппроксимация только
первого порядка.
)
выполняется аппроксимация только
первого порядка.
Задание
1.
Вычислить производную заданной функции
на отрезке
 с точностью
с точностью
 .
Сравнить точность полученных результатов
с точными значениями производной .
.
Сравнить точность полученных результатов
с точными значениями производной .
2.Вычислить производную заданной функции используя интерполяционный многочлен. Сравнить с точными значениями производной.
|
Вариант |
Функция |
Отрезок
|
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|