m08-37

Подставляем полученные данные в формулу расчета коэффициента корреляции Спирмена:

По табл. VIII приложения 1 определяем критические значения коэффициента ранговой корреляции для числа испытуемых n = 11.

rкр = 0,61 для α ≤ 0,05; rкр = 0,76 для α ≤ 0,01.

Полученное эмпирическое значение коэффициента корреляции совпало с критическим значением для уровня значимости α ≤ 0,01.

Ответ: Гипотеза Н0 отвергается, принимается гипотеза Н1. Иными словами, можно утверждать, что показатели психологической готовности к школе и оценки успеваемости первоклассников положительно связаны между собой – чем выше уровень готовности к школе, тем выше показатели школьной успеваемости первоклассников.

Коэффициент корреляции Кендалла τ

Назначение

Коэффициент корреляции Кендалла позволяет определить силу и направление корреляционной связи между двумя признаками или двумя профилями (иерархиями) признаков.

Описание метода

Коэффициент корреляции «τ» (тау) Кендалла относится к числу непараметрических, т. е. при вычислении этого коэффициента не играет роли характер распределения сравниваемых переменных. Как и коэффициент корреляции Спирмена, коэффициент «τ» предназначен для работы с данными, полученными по ранговой шкале. Иногда этот коэффициент можно использовать вместо коэффициента корреляции Спирмена, поскольку способ его вычисления более прост. Он основан на вычислении суммы инверсий и совпадений. В общем виде формула для подсчета рангового коэффициента корреляции Кендалла такова:

где P – число совпадений,

Q – число инверсий,

n – число ранжируемых признаков (черт).

Гипотезы

Н0: Корреляция между переменными (иерархиями) X и Y не отличается от нуля.

Н1: Корреляция между переменными (иерархиями) X и Y достоверно отличается от нуля.

51

Ограничения коэффициента корреляции Кендалла

1.Сравниваемые признаки должны быть измерены в порядковой

шкале.

2.Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.

3.При расчетах этого коэффициента не допускается использование одинаковых рангов.

4.Для оценки уровня достоверности коэффициента «τ» следует пользоваться формулой расчета и таблицей критических значений для t- критерия Стьюдента при df = n – 2.

Алгоритм расчета коэффициента корреляции Кендалла τ

1.Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные X и Y.

2.Проранжировать значения переменной X, начисляя ранг 1 наименьшему значению, в соответствии с правилами ранжирования. То же выполнить для переменной Y.

3.Упорядочить значения рангов переменной Х по возрастанию, соответственно поменяются местами и соответствующие ранги переменной Y. Занести ранги Х в первый столбец таблицы по порядку номеров испытуемых или признаков.

4.Занести ранги переменной Y в соответствующие ячейки второго столбца таблицы.

5.Подсчитать количество совпадений (P) и инверсий (Q). Для этого потребуется тольковторойстолбецтаблицы(порядокранговпеременнойY).

Подсчет совпадений происходит следующим образом: берем самое

верхнее число второго столбца – y1. Подсчитываем, сколько всего чисел, больших y1, встречаются ниже в этом же столбце. Ставим соответствующее значение в соседнюю ячейку в столбце «Совпадения». Затем берем сле-

дующее число y2 – проделываем те же действия и ставим соответствующее значение ниже в соседнюю ячейку в столбце «Совпадения». И так далее.

Для определения количества инверсий опять берем самое верхнее

число второго столбца – y1. Подсчитываем, сколько всего чисел встречаются ниже по столбцу, меньших, чем y1. Ставим соответствующее значение напротив числа y1 в столбце «Инверсия». Берем следующее число y2 – проделываем те же действия и ставим соответствующее значение ниже в соседнюю ячейку в столбце «Совпадения». И так далее.

6.Для проверки правильности подсчета числа инверсий и совпадений используется следующая формула:

52

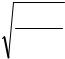
7. Подсчет коэффициента Кендалла может осуществляться по трем тождественным формулам. Первая формула приведена выше. В двух других формулах используются либо Р, либо Q:

8. Проверка уровня значимости коэффициента корреляции с помощью t-критерия Стьюдента по формуле:

где τ – полученное эмпирическое значение коэффициента корреляции. Значение t сопоставляется с критическими значениями t-критерия Стьюдента (tкр) по Табл. X Приложения 1 (число степеней свободы df определяется как df = n – 2). Если выполняется неравенство t ≥ tкр, Н0 отклоняется.

Пример

Психолог предложил супружеским парам проранжировать семь личностных черт, имеющих определяющее значение для семейного благополучия. Необходимо определить, в какой степени совпадают оценки супругов в отношении ранжируемых качеств. Полученные данные приведены в таблице.

Сформулируем гипотезы:

Н0: корреляция между показателями ранжирования обозначенных качеств у супругов не отличается от нуля.

Н1: корреляция между показателями ранжирования обозначенных качеств у супругов статистически значимо отличается от нуля.

Для подсчета коэффициента корреляции «τ» необходимо упорядочить значения второго столбца таблицы (оценки мужа) по возрастанию рангов, в нашем случае от 1 до 7. Соответственно этому поменяются местами как сами черты, так и соответствующие ранги третьего ряда. Оформим эти преобразования в новую таблицу:

53

Рассмотрим, как следует заполнять последние два столбца таблицы. Теперь для работы нам нужен только столбец с рангами, проставленными женой. На его основе заполним последние два столбца таблицы, подсчитав сначала число совпадений.

Подсчет совпадений Р происходит следующим образом: берем самое верхнее число третьего столбца – 5. Подсчитываем, сколько всего чисел, больших 5, встречаются ниже в этом же столбце. Находим их – это 6 и 7. Их всего два. Двойку ставим напротив числа 5 в колонке «Совпадения». Берем затем следующее число 6 – ниже по столбцу и больше его, так же ниже по столбцу, встречается только одно число 7. Ставим напротив 6 в столбце «Совпадения» значение 1. Берем следующее число 7 – больше по величине не может встретиться ни одно число, поскольку 7 – это максимальный ранг. Ставим напротив 7 в столбце «Совпадения» – 0. И т. д.

Для определения количества инверсий Q опять берем самое верхнее число третьего столбца – 5. Подсчитываем, сколько всего чисел встречаются ниже по столбцу, меньших, чем 5. Это числа 4, 3, 2 и 1. Их 4. Ставим напротив числа 5 в столбце «Инверсия» число 4. Берем следующее число 6 – ниже по столбцу и меньше, чем 6, встречаются те же числа, что и для 5. Ставим напротив 6 в столбце «Инверсия» число 4. То же верно и для числа 7. Меньше числа 3 ниже по столбцу встречаются числа 2 и 1. Ставим напротив 3 в столбце «Инверсия» число 2. И так далее.

Проверим правильность подсчета: P +Q = 4 +17 = 21 ;

Следовательно, подсчет числа инверсий и совпадений был произведен правильно.

Проведем подсчет коэффициента корреляции:

Проверим уровень значимости коэффициента корреляции τ с помощью t-критерия Стьюдента по соответствующей формуле:

54

Число степеней свободы в нашем случае будет df = n – 2 = 7 – 2 = 5. По табл. X приложения 1 для df = 5 находим критические значения t-критерия:

tкр = 2,57 для α ≤ 0,05, tкр = 4,03 для α ≤ 0,01.

Неравенство t ≥ tкр не выполняется, соответственно Н0 принимается: коэффициент корреляции «τ» Кендалла достоверно не отличается от нуля. Иными словами, согласованности между супругами в оценке значимых для семейного благополучия личностных черт не обнаружено.

3.5. Параметрические методы сравнения двух выборок

Сравнение двух выборок по признаку, измеренному в метрической шкале, обычно предполагает сравнение средних значений с использованием параметрического t-критерия Стъюдента. Следует различать три ситуа-

ции по соотношению выборок между собой: случай независимых и зависимых выборок (измерений признака) и дополнительно – случай сравнения одного среднего значения с заданной величиной (t-критерий Стьюдента

для одной выборки).

К параметрическим методам относится и сравнение дисперсий двух выборок по F-критерию Фишера. Иногда этот метод приводит к ценным содержательным выводам, а в случае сравнения средних для независимых выборок сравнение дисперсий является обязательной процедурой.

При сравнении средних или дисперсии двух выборок проверяется

ненаправленная статистическая гипотеза о равенстве средних (диспер-

сий) в генеральной совокупности. Соответственно, при ее отклонении допустимо принятие двусторонней альтернативы о конкретном направлении различий в соответствии с соотношением выборочных средних (дисперсий). Для принятия статистического решения в таких случаях применяются двусторонние критерии и, соответственно, критические значения для проверки ненаправленных альтернатив.

Сравнение дисперсий с помощью F-критерия Фишера

Назначение критерия

Метод позволяет проверить гипотезу о том, что дисперсии двух генеральных совокупностей, из которых извлечены сравниваемые выборки, отличаются друг от друга.

55

Описание критерия

Из двух генеральных совокупностей случайно извлекаются две независимые выборки объемами n1 и n 2 с нормальным распределением изучаемого признака. По результатам исследования подсчитываются оценки дисперсий S12 и S 22 . Требуется сравнить эти дисперсии.

Гипотезы

Н0: Выборки 1 и 2 принадлежат генеральным совокупностям с одинаковыми генеральными дисперсиями: S12 = S 22 = S 2 .

H1: Выборки 1 и 2 принадлежат генеральным совокупностям с разными дисперсиями: S12 ≠ S 22 .

Ограничения

Распределения признака и в той, и в другой выборке существенно не отличаются от нормального. Критерий Фишера очень чувствителен к отклонениям распределения данных от нормального. Если вид распределения неизвестен, или проводились порядковые измерения, результаты могут оказаться ошибочными.

Алгоритм расчета F-критерия Фишера3

1.Вычислить значения дисперсий S12 и S 22 для выборок n1 и n 2 .

2.Вычислить эмпирическое значение F – отношение большей дисперсии к меньшей:

F = SБ2 . Sм2

3. Определить критические значения распределения Фишера Fα (df1; df2) для чисел степеней свободы df1 = n Б −1; df2 = n М −1. На первом месте в

Fα (df1; df2) всегда стоит число степеней свободы для большей выборочной дисперсии.

4. Сравнить эмпирическое значение F с критическими значениями по табл. IX приложения 1.

Если Fэмп < Fα (df1; df2), то нулевая гипотеза о равенстве двух генеральных дисперсий принимается. В этом случае обе выборки могут быть объединены в одну, и по двум выборочным дисперсиям можно оценить генеральную дисперсию S 2 :

Если эмпирические значения критерия попадают в критическую область критерия, т. е. если Fэмп ≥ Fα (df1; df2), нулевая гипотеза (Н0) отвергается и принимается альтернативная (Н1).

3 Перед применением критерия необходимо проверить нормальность распределения данных, рассчитав эмпирические и критические значения асимметрии и эксцесса (см. п. 2.2).

56

Метод может применяться для проверки предположения о равенстве (гомогенности) дисперсий перед проверкой достоверности различия средних по t-критерию Стьюдента для независимых выборок разной численности. Однако содержательная интерпретация статистически достоверного различия дисперсий может иметь и самостоятельную ценность.

Пример

Детям предлагались обычные арифметические задания, после чего одной случайно выбранной половине учащихся сообщали, что они не выдержали испытания, а остальным – обратное. Затем у каждого ребенка спрашивали, сколько секунд ему потребовалось бы для решения аналогичной задачи. Экспериментатор вычислял разность между называемым ребенком временем и результатом выполненного задания (в секундах). Ожидалось, что сообщение о неудаче вызовет некоторую неадекватность самооценки ребенка. Проверяемая гипотеза состояла в том, что дисперсия совокупности самооценок не зависит от сообщений об удаче или неудаче

(H0 : S12 = S 22 ).

Получены следующие данные:

2. Определим критические значения распределения Фишера Fα (df1; df2) для чисел степеней свободы: df1 = n Б −1 = 12 – 1; df2 = n М −1 = 12 – 1.

2,97 (α ≤ 0,05)

Fкр = ( )

4,85 α ≤ 0,01

3. Для принятия статистического решения сравним эмпирическое и критическое значения критерия: Fэмп > Fкр (α < 0,01)

Ответ: H0 отвергается; принимается Н1: дисперсия в группе 1 превышает дисперсию в группе 2 (α < 0,01). Следовательно, после сообщения о неудаче неадекватность самооценки выше, чем после сообщения об удаче.

57

Сравнение средних значений с помощью t-критерия Стьюдента

Назначение критерия

Параметрический критерий Стьюдента позволяет сравнить два выборочных средних значения.

Описание критерия

Из двух нормальных генеральных совокупностей извлекаются независимые выборки объемами n1 и n 2 с нормальным распределением изучаемого признака. По результатам исследования подсчитываются выборочные средние значения и дисперсии: М1 , М2 и S12 , S 22 . Требуется сравнить средние значения.

Гипотезы

Н0: Математическое ожидание (среднее значение) в выборке 1 не превышает математического ожидания в выборке 2 (М1 = М2 ).

H1: Математическое ожидание в выборке 1 превышает математическое ожидание в выборке 2 (М1 > М2 ).

Ограничения критерия t

Нормальное распределение признака в исследуемой выборке. В противном случае следует применить непараметрические критерии (G- критерий знаков, U-критерий Манна – Уитни).

Алгоритм расчета t-критерия Стьюдента 4

1.Вычислить дисперсии с помощью критерия Фишера.

2.В случае равенства дисперсий (S12 = S 22 ) для проверки нулевой ги-

потезы эмпирическое значение t вычисляется по формуле:

где М1 – математическое ожидание выборки 1; М2 – математическое ожидание выборки 2;

S – среднеквадратическое отклонение, взвешенное по числам степеней свободы dfi = ni −1:

В случае если дисперсии не равны (S12 ≠ S 22 ), эмпирическое значение критерия Стьюдента вычисляется по формуле:

4 Перед применением критерия необходимо проверить нормальность распределения данных, рассчитав эмпирические и критические значения асимметрии и эксцесса (см. п. 2.2).

58

3. Вычисленное эмпирическое значение сопоставляется с критическим значением, определяемым в зависимости от уровня значимости α и числа степеней свободы df =df1+ df2 = n1 + n2 – 2, по табл. X приложения 1.

Если эмпирическое значение критерия меньше критического (׀t׀ < tкр), принимается нулевая гипотеза (H0). Если эмпирическое значение равно или превышает критическое (׀t׀ ≥ tкр), H0 отвергается и принимается альтернативная гипотеза Н1.

Пример

Для выявления различий в уровне интеллекта студентов 1-го и 5-го курсов случайным образом были отобраны 30 студентов 1 курса и 28 студентов 5 курса, у которых интеллект определялся с помощью одной и той же методики. Полученные результаты представлены в таблице.

Сопоставив эмпирическое и критические значения дисперсии для чисел степеней свободы df1 = n Б −1 = 28 – 1 = 27; df2 = n М −1 = 30 – 1 = 29, делаем вывод о равенстве дисперсий (Fэмп < Fкр (α < 0,05)).

2. Определяем значение S – среднеквадратического отклонения:

3. ВычисляемэмпирическоезначениекритерияСтьюдентапоформуле:

4. Определяем критическое значение критерия Стьюдента для числа степеней свободы df =df1+ df2 = 29 + 27 = 56:

59

2,003(α ≤ 0,05) tкр = 2,667(α ≤ 0,01).

Принимаем статистическое решение и формулируем вывод. Сопоставив эмпирическое и критическое значения критерия, получаем: ׀t׀ > tкр (α < 0,01). Соответственно, нулевая гипотеза отвергается, принимается альтернативная Н1. Уровень интеллекта у студентов 5-го курса статистически достоверно выше, чемустудентов1-гокурса(α< 0,01).

60