m08-37

Проверим это. Поскольку нас интересует факт решения задачи, будем считать «эффектом» успех в решении экспериментальной задачи, а отсутствием эффекта – неудачу в ее решении.

Сформулируем гипотезы.

H0: Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй группе.

Н1: Доля лиц, справившихся с задачей, в первой группе больше, чем во второй группе.

Теперь построим так называемую четырехклеточную, или четырехпольную таблицу, которая фактически представляет собой таблицу эмпирических частотподвумзначениямпризнака: «естьэффект» – «нетэффекта».

Четырехклеточная таблица для расчета критерия при сопоставлении двух групп испытуемых по процентной доле решивших задачу

В четырехклеточной таблице, как правило, сверху размечаются столбцы «Есть эффект» и «Нет эффекта», а слева – строки «1 группа» и «2 группа». Участвуют в сопоставлениях, собственно, только процентные доли по столбцу «Есть эффект».

По Табл. V Приложения 1 определяем величины φ, соответствующие процентным долям в каждой из групп.

φ1 (60 %) = 1,772

φ2 (40 %) = 1,369

Теперь подсчитаем эмпирическое значение φ* по формуле:

где φ1 – угол, соответствующий большей % доле; φ2 – угол, соответствующий меньшей % доле; n1 – количество наблюдений в выборке 1;

n 2 – количество наблюдений в выборке 2. В данном случае:

По табл. VI приложения 1 определяем, какому уровню значимости соответствует φ*эмп = 1,34; ρ = 0,09.

41

Можно установить и критические значения φ*, соответствующие принятым в психологии уровням статистической значимости:

1,64 (ρ ≤ 0,05 ) φ*кр = 2,31(ρ ≤ 0,01)

φ*эмп = 1,34; φ*эмп < φ*кр

Полученное эмпирическое значение φ* находится в зоне незначимости. Ответ: H0 принимается. Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй группе.

3.4. Корреляционный анализ

Исследователя в области психологии и педагогики нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых группах. Например, могут ли учащиеся с высоким уровнем тревожности демонстрировать стабильные академические достижения, или связана ли продолжительность работы социального педагога в школе с уровнем его профессионального выгорания, или с чем больше связан уровень умственного развития учащихся – с их успеваемостью по математике или по литературе и т. п.? Для решения подобного рода задач применяется корреляционный анализ.

Корреляционный анализ – комплекс методов статистического исследования взаимозависимости между переменными, связанными корреляционными отношениями.

Корреляционная связь (лат. correlatio – связь, зависимость) – это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого.

Корреляционная связь между двумя признаками может свидетельствовать не о зависимости их между собой, а о зависимости обоих этих признаков от какого-то третьего признака или сочетания признаков, не рассматриваемых в исследовании. Корреляционные связи свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого.

Виды корреляционных связей между измеренными признаками могут быть различны: так, корреляция бывает линейной и нелинейной, положительной и отрицательной. Она линейна, если с увеличением или уменьшением одной переменной X, вторая переменная Y в среднем либо также растет, либо убывает. Она нелинейна, если при увеличении одной величины характер изменения второй не линеен, а описывается другими законами.

Корреляция будет положительной, если с увеличением переменной X переменная Y в среднем также увеличивается, а если с увеличением X переменная Y имеет в среднем тенденцию к уменьшению, то говорят о наличии отрицательной корреляции. Возможна ситуация, когда между переменными

42

невозможно установить какую-либо связь. В этом случае говорят об отсутствии корреляционной связи. При положительной корреляции коэффициент корреляции имеет положительный знак (например, r = 0,207), при отрицательной корреляции – отрицательный знак (например, r = −0,207). Знак ко-

эффициента корреляции очень важен для интерпретации полученной связи. Если знак коэффициента линейной корреляции – «плюс», то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует бóльшая величина другого признака (другой переменной). Иными словами, если один показатель увеличивается, то соответственно увеличивается и другой показатель. Такая связь носит название прямо пропорциональной. Если же получен знак «минус», то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака «минус», увеличению одной переменной соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости.

Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции. Максимальное возможное абсолютное значение коэффициента корреляции r = 1,00; минимальное – r = 0. Используются две системы классификации корреляционной связи по их силе: общая и частная. Общая классификация корреляционных связей (по Э.В. Ивантер, А.В. Коросову):

Частная классификация корреляционных связей ориентируется на объем выборки и уровень статистической значимости:

Обычно принято ориентироваться на вторую классификацию. Она определяет, какого уровня значимости достигает данная величина коэффициента корреляции при данном объеме выборки. Чем больше объем выборки, тем меньшей величины коэффициента корреляции оказывается достаточно, чтобы корреляция была признана достоверной.

Переменные X и Y могут быть измерены в разных шкалах, именно это определяет выбор соответствующего коэффициента корреляции. Пред-

43

ставим соотношения между типами шкал, в которых могут быть измерены переменные X и Y и соответствующими мерами связи в виде таблицы:

Коэффициент корреляции Пирсона rxy

Назначение

Коэффициент корреляции Пирсона позволяет определить силу и направление корреляционной связи между двумя признаками.

Описание метода

Для подсчета коэффициента корреляции Пирсона необходимо располагать двумя рядами значений. Такими рядами значений могут быть:

–два признака, измеренные в одной и той же группе испытуемых;

–два ряда значений по одному и тому же признаку, полученные в двух группах испытуемых.

Расчет коэффициента корреляции Пирсона предполагает, что переменные Х и Y измерены в интервальной шкале и распределены нормально.

В общем виде формула для подсчета коэффициента корреляции такова:

=) (yi − y−)y)2 , (1)rxy ∑(xi − x∑(xi − x )2 ∑(yi

где xi – значения, принимаемые переменной X, yi – значения, принимаемые переменной Y,

x– среднее значение по Х,

y– среднее значение по Y.

Для удобства расчетов данная формула может быть преобразована в следующий вид:

44

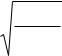
где xi – значения, принимаемые переменной X, yi – значения, принимаемые переменной Y,

n – количество пар сопоставляемых признаков.

Гипотезы

Н0: Корреляция между переменными X и Y не отличается от нуля. Н1: Корреляция между переменными X и Y достоверно отличается от

нуля.

Ограничения коэффициента корреляции Пирсона

1.Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.

2.Распределения переменных X и Y должны быть близки к нормальному.

3.Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.

4.По каждой переменной должно быть представлено не менее 5 наблюдений. Верхняя граница выборки определяется имеющимися таблицами критических значений, а именно n ≤ 5000.

Алгоритм расчета коэффициента корреляции Пирсона rxy

1.Определить, какие два признака будут участвовать в сопоставлении как переменные X и Y.

2.Занести значения переменных X и Y в таблицу.

3.Рассчитать произведение переменных X и Y и занести в соответствующий столбец.

4.Подсчитать значение каждой переменной (отдельно X и Y) в квадрате и занести в таблицу.

5.Подсчитать в нижней строке таблицы сумму каждой переменной, сумму квадратов каждой переменной и сумму последовательных произведений переменных друг на друга в соответствующих ячейках.

6.Подставить полученные значения в формулу (2).

7.Определить статистическую значимость полученного коэффициента корреляции. Для этого необходимо установить по табл. VII приложе-

ния 1 критические значения rxy для данного n. Если rxy превышает критическое значение или по крайней мере равен ему, корреляция достоверно

отличается от нуля (Н0 отвергается).

Статистическая значимость коэффициента rxy может также рассчитываться с помощью критерия Стьюдента (t):

гдеrxy – полученноеэмпирическоезначениекоэффициентакорреляции.

45

Значение t сопоставляется с критическими значениями t-критерия Стьюдента по соответствующей таблице (число степеней свободы df определяется как df = n – 2). Если выполняется неравенство t ≥ tкр, Н0 отклоняется.

Пример

20 школьникам предлагались тесты, направленные на изучение на- глядно-образного и вербального мышления. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли связь между временем решения задач на наглядно-образное и вербальное мышление? Переменная X обозначает среднее время решения на- глядно-образных, а переменная Y – среднее время решения вербальных заданий тестов. Данные представлены в таблице.

Сформулируем гипотезы:

Н0: корреляция между временем решения задач на нагляднообразное и вербальное мышление не отличается от нуля.

Н1: корреляция между временем решения задач на наглядно-образное и вербальное мышление статистически значимо отличается от нуля.

Произведем необходимые расчеты согласно алгоритму. В таблице даны индивидуальные значения переменных X и Y, построчные произведения переменных Х и Y, квадраты переменных всех индивидуальных значений переменных X и Y, а также суммы всех вышеперечисленных величин.

46

Рассчитываем эмпирическую величину коэффициента корреляции по формуле, подставляя соответствующие значения:

Определяем критические значения коэффициента линейной корреляции Пирсона по Табл. VII Приложения 1. Особо отметим, что в табл. VII величины критических значений даны по абсолютной величине. Следовательно, оценка уровня значимости коэффициента проводится без учета знака, полученного при расчете эмпирического значения, а знак добавляется для дальнейшей интерпретации характера связи между переменными X и Y.

Итак, критические значения коэффициента корреляции Пирсона для n = 20 составляют:

rкр = 0,44 для α ≤ 0,05; rкр = 0,56 для α ≤ 0,01.

Рассчитаем также статистическую значимость полученного эмпирического значения коэффициента корреляции с помощью t-критерия Стьюдента:

По табл. X приложения 1 находим критические значения в соответствии с числом степеней свободы df = 20 – 1 = 18:

tкр = 2,101 для α ≤ 0,05; tкр = 2,878 для α ≤ 0,01.

Неравенство t ≥ tкр выполняется при α ≤ 0,01, соответственно гипотеза Н0 отклоняется и принимается Н1.

Ответ: Связь между временем решения наглядно-образных и вербальных задач статистически значима (α ≤ 0,01) и является положительной: чем выше среднее время решения наглядно-образных задач, тем выше среднее время решения вербальных, и наоборот.

47

Коэффициент корреляции Спирмена rs

Назначение

Коэффициент корреляции Спирмена позволяет определить силу и направление корреляционной связи между двумя признаками или двумя профилями (иерархиями) признаков.

Описание метода

Коэффициент ранговой корреляции универсален: он применим к любым количественно измеренным или ранжированным данным. Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин.

Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы. Такими рядами значений могут быть:

1)два признака, измеренные в одной и той же группе испытуемых;

2)две индивидуальные иерархии признаков, выявленные у двух ис-

пытуемых по одному и тому же набору признаков (например, личностные профили по 16-факторному опроснику Р.Б. Кеттелла, последовательности предпочтений в выборе из нескольких альтернатив и др.);

3)две групповые иерархии признаков;

4)индивидуальная и групповая иерархии признаков.

Вначале показатели ранжируются отдельно по каждому из признаков. Как правило, меньшему значению признака начисляется меньший ранг.

Формула для подсчета рангового коэффициента корреляции Спирмена:

∑(d 2 )

rs =1−6 n (n2 −1),

где n – количество ранжируемых признаков,

d – разность между рангами по двум переменным для каждого испытуемого,

∑(d 2 ) – сумма квадратов разностей между рангами.

Гипотезы

Возможны два варианта гипотез. Первый относится к случаю 1, второй – к трем остальным случаям.

Первый вариант гипотез:

Н0: Корреляция между переменными X и Y не отличается от нуля. Н1: Корреляция между переменными X и Y достоверно отличается от

нуля.

48

Второй вариант гипотез:

Н0: Корреляция между иерархиями X и Y не отличается от нуля. Н1: Корреляция между иерархиями X и Y достоверно отличается от

нуля.

Ограничения коэффициента корреляции Спирмена

1.По каждой переменной должно быть представлено не менее 5 наблюдений. Верхняя граница выборки определяется имеющимися таблицами критических значений, а именно n ≤ 40. В случае использования большего, чем 40, числа ранжируемых признаков, уровень значимости коэффициента корреляции следует определять по табл. VII приложения 1 для коэффициента корреляции Пирсона.

2.Коэффициент ранговой корреляции Спирмена rs, при большом количестве одинаковых рангов по одной или обеим сопоставляемым переменным дает огрубленные значения. В идеале оба коррелируемых ряда должны

представлять собой две последовательности несовпадающих значений. В случае, если это условие не соблюдается, необходимо вносить поправку на одинаковые ранги.

Алгоритм расчета коэффициента корреляции Спирмена rs

1.Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные X и Y.

2.Проранжировать значения переменной X, начисляя ранг 1 наи-

меньшему значению, в соответствии с правилами ранжирования (см. п. 3.1). Занести ранги в первую графу таблицы по порядку номеров испытуемых или признаков.

3.Проранжировать значения переменной Y, в соответствии с теми же правилами. Занести ранги во вторую графу таблицы по порядку номеров испытуемых или признаков.

4.Подсчитать разности d между рангами X и Y по каждой строке таблицы и занести в третий столбец таблицы.

5.Возвести каждую разность в квадрат: d2. Эти значения занести в четвертый столбец таблицы.

6.Подсчитать сумму квадратов Σ(d²).

7.При наличии одинаковых рангов рассчитать поправки:

Tx = ∑(x3 − x)12 ,

Ty = ∑(y3 − y)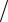12 ,

где x – объем каждой группы одинаковых рангов в ранговом ряду X, y – объем каждой группы одинаковых рангов в ранговом ряду Y.

8. Рассчитать коэффициент ранговой корреляции rs при отсутствии одинаковых рангов по формуле, приведенной выше.

49

При наличии одинаковых рангов формула расчета коэффициента ранговой корреляции Спирмена будет несколько иной:

rs =1−6 ∑(d 2()+2 T−x +)Ty , n n 1

где ∑(d 2 ) – сумма квадратов разностей между рангами,

Тx и Тy – поправки на одинаковые ранги,

n – количество испытуемых или признаков, участвовавших в ранжировании.

9. Определить по табл. VIII приложения критические значения rs для данного n. Если rs превышает критическое значение или по крайней мере равен ему, корреляция достоверно отличается от нуля (Н0 отклоняется).

Пример

Психолог выясняет, как связаны между собой индивидуальные показатели психологической готовности к школе, полученные вначале обучения в школе у одиннадцати первоклассников, и их средняя успеваемость в конце первого учебного года.

Сформулируем гипотезы:

Н0: корреляция между показателями готовности к школе и средней успеваемостью не отличается от нуля.

Н1: корреляция между показателями готовности к школе и средней успеваемостью статистически значимо отличается от нуля.

Для решения этой задачи были проранжированы значения показателей школьной готовности, полученные при поступлении в школу, и средние значения итоговых показателей успеваемости в конце года у этих же учащихся. Результаты представим в таблице.

50