Методика работы над заданиями стохастического характера

В содержании стохастической содержательно-методической линии выделяются (Г.С. Евдокимова, А. Плоцки, В.Д. Селютин, С.А. Самсонова и др.) три взаимосвязанных направления, методикой работы над которыми должен владеть будущий учитель:

 подготовка младших школьников в области комбинаторики, с целью создания в дальнейшем аппарата для решения вероятностных задач и логического развития учащихся;

 формирование первоначальных представлений о случайных событиях, о вероятностях событий;

 подготовка в области математической статистики: формирование умений, связанных с представлением, сбором данных и их интерпретацией.

Методика работы над заданиями вероятностного характера

Если умение решать простейшие комбинаторные задачи является требованием Государственного образовательного стандарта основного общего образования к уровню подготовки младшего школьника, то основные понятия теории вероятностей и математической статистики являются пропедевтическими.

Знакомство с элементами теории вероятностей в начальной школе начинается с формирования на интуитивном уровне представлений об опыте и понятий случайного события и его вероятности. Такой подход не требует введения в программное содержание этих новых понятий. Они связываются с известными из жизни словами – часто, редко, всегда, никогда, «это случится наверняка», «это невозможно», «ни в коем случае», «возможно да, возможно нет» и другими, определяющими частоту наступления случайных событий.

На первом этапе формирования первоначальных стохастических преставлений целесообразно обратить внимание младших школьников на неоднозначность и изменчивость многих явлений, познакомить учащихся со случайными явлениями, научить интуитивно отличать их от строго детерминированных, различать достоверные и невозможные события, «более возможные», и «менее возможные» события.

Методисты (А. Плоцки, В.Д. Селютин, С.А. Самсонова) подчеркивают, что только наблюдений и интуитивных представлений оказывается недостаточно для изучения вероятностных понятий. Чтобы сформировать у школьников первоначальные вероятностно-статистические представления, необходимо не только знакомить их с самими реальными явлениями стохастической структуры, но и организовать изучение свойств этих явлений. Это послужит основой для дальнейшего обобщения и систематизации первоначальных стохастических представлений, создаст благоприятные условия для успешного изучения в дальнейшем математических моделей случайных явлений и процессов, для приобретения умений использования вероятностных методов при решении практических задач. Поэтому первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании, то есть в проведении многочисленных опытов с разнородными предметами (игральными костями, волчками, монетами, шарами и т. д.).

Эксперимент повторяется много раз при одних и тех же условиях, а учащимся предлагают пытаться угадывать результат.

Рассмотрим некоторые задания, которые могут быть предложены младшим школьникам на данном этапе.

Задание. Подбросим игральный кубик. Как вы думаете, какое событие никогда не произойдёт: а) выпадет число меньшее 6; б) выпадет число 4; в) выпадет число большее 6?

После нескольких раз повторения данного эксперимента учащиеся пытаются ответить на поставленный вопрос. Эксперимент повторяется много раз при одних и тех же условиях, а младшим школьникам предлагают угадывать результат. В результате эксперимента происходит событие (выпадение определенного числа), причем учащиеся участвуют в этом непосредственно.

Задание. Соня написала слова: математика, лабиринт, диаграмма, линия. Посчитай число букв в словах. Какая буква встречается чаще, реже?

В этом задании можно вести речь о гласных и согласных буквах, либо обо всех буквах, используемых в этих словах.

Задание. В мешке имеется 2 белых и 1 черный шар. Извлечем из мешка, два шара. Как вы думаете, какое событие никогда не произойдёт: а) извлеченные шары белые; б) извлеченные шары черные; в) извлеченные шары разного цвета; г) извлечены шары зеленого цвета?

Приведем пример «вероятностной» задачи из учебника «Моя математика» для 2-го класса, часть 3, авторского коллектива Т.Е. Демидовой, С.А. Козловой, А.П. Тонких.

Задание. (Задача № 8, стр.3) «Положи в мешочек из непрозрачного материала три одинаковых шарика: 2 белых и 1 черный. Достань, не глядя, один шарик. Запомни его цвет и положи обратно. Проведи этот опыт 10 раз. Сделай вывод о том, шарик какого цвета ты доставал чаще».

Работа может быть организована следующим образом. Опыт состоит в том, что нужно достать, не глядя (то есть случайным образом), из мешочка, содержащего три шара, один шар, запомнить его цвет и вернуть обратно. Повторить этот опыт 10 раз. Условия, в которых необходимо провести опыт:

 шары должны быть по размеру одинаковыми;

 выбирать нужно один шар, не глядя внутрь мешочка;

 мешочек должен быть из непрозрачного материала, чтобы цвет вынимаемого шара от экспериментатора был скрыт.

В процессе работы с элементами теории вероятностей появляется такое понятие, как «неразличимые объекты». Вопрос о том, когда два предмета следует считать «неразличимыми» достаточно сложен. Например, при игре в карты мы можем рассматривать как «неразличимые» или «сходные» две карты масти «пик» (туз и семерка) или два туза (туз пик и туз треф). Опыт показывает, что учащиеся лучше схватывают эту идею, если условлено, что два объекта являются неразличимыми, несмотря на то, что они таковыми совсем не являются.

Следует добиться от учащихся четкого понимания того, что им предстоит делать и в каких условиях. После этого можно предложить младшим школьникам спрогнозировать ответ предлагаемого опыта: «Можно ли предсказать, какого цвета шар будет выниматься чаще?» При ответах учащихся следует обратить внимание на приводимую ими аргументацию. Обсудив гипотезы, предложенные младшими школьниками, учитель делает обобщение: «Мы обсудили шансы более частого появления белого (черного) шара, но лишь по окончании опыта станет ясно, шар какого цвета появлялся чаще и насколько верны наши прогнозы».

Далее проводим опыт, не забывая каждый раз фиксировать, какого цвета был вынутый шар. После завершения опыта на основе полученных данных учащиеся делают вывод о том, шар какого цвета они доставали чаще. Важно вернуться к тем аргументам, которые были высказаны на этапе прогноза, выделить те, которые были вполне логичны и разумны и соответствуют полученному результату. Такое интуитивное предвидение результата испытания может лишь подтвердить понимание смысла случайных событий.

В ходе обсуждения различных аналогичных задач учащиеся убеждаются в том, что в мире случайных событий можно найти некоторые закономерности и оценить шансы наступления различных событий.

Второй этап состоит в том, что младшим школьникам предлагают игры, в которых можно качественным образом сравнивать вероятности некоторых событий.

Следующий эксперимент можно использовать при знакомстве с понятиями: равновозможные события, более вероятное событие, менее вероятное событие.

Задание. В мешке имеется 2 белых и 1 черный шар. Извлечем из мешка, два шара. Как вы думаете, каким может быть результат такого опыта?

Обнаруживается, что может быть 3 случая:

С помощью эксперимента необходимо выяснить, какой из этих случаев более возможен, менее возможен или, может быть, среди них имеются равновозможные случаи. Затем полученные экспериментальные выводы необходимо обосновать, рассмотрев все возможные комбинации выбора двух шаров из имеющихся трех.

Целесообразно задать вопрос: сколько шаров нужно вытянуть из мешка, чтобы наверняка иметь шары двух цветов?

Учащимися могут быть предложены различные значения, но им необходимо обосновать свой выбор. В результате проведения экспериментов необходимо подвести их к следующим выводам:

 если вынуть 3 шара, наверняка будет шары двух цветов;

 если вынуть 2 шара, то возможно, но необязательно будут шары двух цветов;

 если вынуть 1 шар, то невозможно получить шары двух цветов.

Задание. В мешке имеется 3 красных, 3 белых и 3 зелёных шара. Сколько шаров нужно вытянуть из мешка, чтобы наверняка иметь шары трёх цветов?

Проводя эксперименты, учащиеся должны прийти к следующим выводам:

 если вынуть 7,8,9 шаров, наверняка будут шары трёх цветов;

 если вынуть 3,4,5 или 6 шаров, то возможно, но необязательно будут шары трёх цветов;

 если вынуть 1 или 2 шара, то невозможно получить шары трёх цветов.

Разумно исследовать, в каком из случаев имеется наибольшая возможность получить шары трёх цветов  если вытащить 3, или 4, или 5, или 6 шаров. Можно ввести и термины «более вероятно», «менее вероятно».

Следующие задания предложены студентами нашего факультета для проведения игрового урока с элементами стохастики.

Задание. Лев Алекс, зебра Марти, жираф Мелман и гиппопотам Глория попадают на остров Мадагаскар. Перед ними открывается таинственный мир дикой природы. Друзья решили обследовать остров. Пробираясь сквозь джунгли, жираф Мелман «наткнулся» на цветочную поляну и решил сделать сюрприз для Глории, зная, что ей нравятся цветы синего цвета.

На поляне растут 5 желтых, 3 красных и 4 синих цветка. Сколько цветков нужно сорвать Мелману, чтобы наверняка иметь синий цветок, если он не различает цвета?

Работа над заданием.

− Прочитайте задачу. Какие цветы растут на поляне? (На поляне растут желтые, красные и синие цветы.)

− Сколько желтых цветов растет на поляне? (На поляне растет 5 желтых цветов.)

− Сколько красных цветов растет на поляне? (На поляне растет 3 красных цветка.)

− Сколько цветов синего цвета растет на поляне? (На поляне растет 4 цветка синего цвета.)

− Что еще говорится в задаче? (Мелман не различает цвета.)

− Что требуется узнать в задаче? (Сколько цветков нужно сорвать Мелману, чтобы наверняка иметь синий цветок?)

− Если Мелман возьмет один цветок, обязательно ли он будет иметь синий цветок? Почему? (Нет, необязательно, так как он может взять красный или желтый цветок.)

− Если Мелман возьмет два цветка, обязательно ли среди них окажется синий цветок? Почему? (Синий цветок может оказаться у Мелмана, но не обязательно, так как у него может быть и 1 красный, а 1 желтый, и 2 красных, и 2 желтых цветы, а синего не быть вовсе.)

Аналогичны рассуждения с 3, 4, 5, 6, 7 и 8 цветками.

− Если Мелман возьмет 9 цветков, может ли среди них наверняка оказаться синий цветок? (Если Мелман возьмет 9 цветков, то среди них наверняка окажется синий цветок. Например, у него из 9 цветков могут оказаться 3 красных и 5 желтых цветков, тогда 1 цветок будет наверняка синим.)

Аналогично, если взять 10, 11 и 12 цветков.

− Так какой же ответ мы предложим Мелману?

Ответ. Чтобы у Мелмана наверняка оказался синий цветок, он должен взять либо 9, либо 10, либо 11, либо 12 цветков.

− А какое минимальное количество цветов должно быть у Мелмана, чтобы среди них наверняка был синий цветок? ( Чтобы у Мелмана наверняка оказался цветок синего цвета, он должен взять минимум 9 цветков.)

Задание. У гиппопотама Глории в кошельке 2 монеты по 1 рублю, 3 монеты по 2 рубля и 3 монеты по 5 рублей. Сколько минимум монет ей нужно вынуть, не глядя в кошелек, чтобы наверняка хватило оплатить проезд за троих, если стоимость проезда 5 рублей?

Работа над заданием.

− Прочитайте задачу еще раз. Сколько монет было в кошельке Глории? (В кошельке Глории было 2 монеты по 1 рублю, 3 монеты по 2 рубля и 3 монеты по 5 рублей.)

− Каким образом она должна достать монеты? (Она должна достать монеты, не глядя в кошелек.)

−Что нужно узнать в задаче? (Сколько минимум монет ей нужно вынуть, чтобы наверняка хватило оплатить проезд за троих?)

− Сколько рублей должно оказаться у Глории? (Не известно, но известно количество пассажиров и стоимость проезда одного пассажира.)

− Как найти стоимость проезда троих пассажиров? (Стоимость проезда одного пассажира умножим на количество пассажиров. (3∙5=15) Стоимость проезда троих пассажиров равна 15 рублям.)

− Какое минимальное количество рублей должна взять, не глядя в кошелек, Глория? (Глория должна взять 15 рублей.)

− Решим нашу задачу, осуществляя систематический перебор. Если Глория вынет одну монету, сколько рублей может у нее оказаться? (1 рубль, или 2 рубля, или 5 рублей.)

− Хватит ей денег, чтобы оплатить проезд? (Нет, так как ей нужно 15 рублей.)

− Сколько рублей может оказаться у Глории, если она возьмет 2 монеты? (2 рубля (1+1=2) или 3 рубля (1+2=3), или 6 рублей (1+5=6), или 4 рубля (2+2=4), или 7 рублей (2+5=7), или 10 рублей (5+5=10).)

− Хватит ли Глории денег, чтобы оплатить проезд? ( Нет.)

− Если Глория вынет три монеты, сколько денег может у нее оказаться? (У Глории может оказаться 4 рубля (1+1+2=4) или 7 рублей (1+1+5=7), или 5 рублей (1+2+2=5), или 11 рублей (1+5+5=11), или 6 рублей (2+2+2=6), или 9 рублей (2+2+5=9), или 12 рублей (2+5+5=12), или 15 рублей (5+5+5=15).)

−Хватит Глории денег оплатить проезд? ( Может быть хватит, а может и нет.)

−Обязательно ли Глория, взяв 3 монеты, оплатит проезд? Почему? (Нет, потому что она может взять меньше 15 рублей.)

Аналогично, если вынуть 4, 5 и 6 монет.

− Вынув 7 монет, сколько денег может иметь Глория? (18 рублей (1+1+2+2+2+5+5=18).)

− Если Глория вынет такое количество монет, обязательно ли у нее окажется нужная сумма? (Да, так как, вынув 7 монет, Глория будет иметь 18 рублей, а этого достаточно, чтобы оплатить проезд.)

− Значит, сколько монет должна взять Глория из кошелька, чтобы ей наверняка хватило оплатить проезд? (7 монет.)

Ответ. 7 монет.

При сравнении вероятностей наступления событий, с увеличением числа объектов в задачах, целесообразно использовать таблицы и графы, позволяющие упросить рассуждения.

Дерево возможных вариантов (дерево возможностей) при необходимости легко преобразуется в стохастическое дерево. Граф-дерево используют для упорядочения вариантов при решении комбинаторных задач. Стохастическое дерево является связующим элементом между комбинаторной и вероятностной составляющими новой содержательно-методической линии А. Плоцки обращает внимание на важную роль стохастического графа как особенного средства математизации и построения умозаключений¹².

Приведем примеры.

Задание. В мешке имеется 2 белых и 1 черный шар. Какое событие более вероятно «оба вынутых шара одинакового цвета» или «вынутые шары разных цветов»?

Определим, сколько шаров нужно вытянуть из мешка, чтобы наверняка иметь шары двух цветов, с помощью дерева возможностей. Два последовательных извлечения могут привести к следующим исходам:

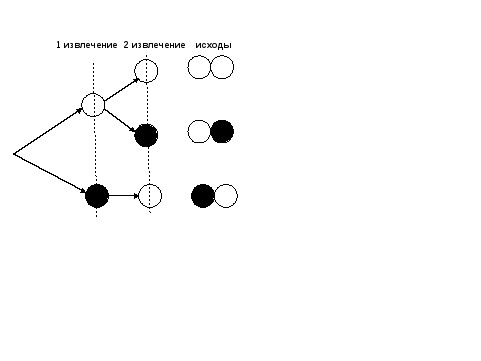Рис.7

В данном случае событие «оба вынутых шара одинакового цвета», менее вероятно, чем событие «вынутые шары разных цветов».

Заметим, что на данной стадии младшие школьники уже могут проводить сравнение вероятностей. Вопрос о числовой характеристике вероятности является целью третьего этапа.

Формирование у школьников представления о вероятности осуществляется аналогично знакомству учащихся с понятием «дробь». Сначала определим общее количество шаров (2+1=3). Допустим, необходимо найти вероятность того, что извлеченный шар будет белым. Количество белых шаров равно 2, общее количество шаров − 3, тогда вероятность того, что извлеченный шар будет белым равна 2/3. Аналогично проводится вычисление вероятности того, что извлеченный шар будет черного цвета. Затем можно сравнить эти вероятности, то есть 2/3>1/3, и продемонстрировать это экспериментально.

Рассмотрим, как изменится ситуация, если извлеченный шар возвращать в мешок.

Задание. В мешке имеется 2 белых и 1 черный шар. Какое событие более вероятно «оба вынутых шара одинакового цвета» или «вынутые шары разных цветов»?

Используя дерево возможностей, видим, что в этом случае, 2 последовательных извлечения могут привести к следующим исходам:

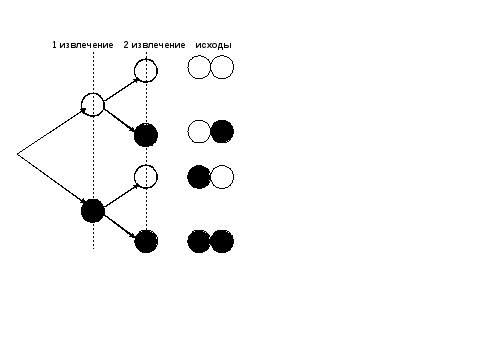Рис.8

В данном случае события: «оба вынутых шара одинакового цвета» и «вынутые шары разных цветов» − равновероятны.

Одним из средств систематизации полученных в наблюдениях данных являются таблицы, позволяющие без дополнительных расчетов сопоставить различные показатели выявить характерные особенности изучаемых явлений. Сведения располагаются в таблице рядами и столбцами, что дает возможность легко охватить их взглядом и сравнить между собой.

Когда материал приведен в систему, определено относительное значение каждого признака, тогда уже можно выяснить, какие признаки совпадают, что именно характеризуют те или иные из них, тогда-то возможно определить, есть или нет порядок и последовательность между явлениями, сопровождается ли один признак другим, и если да, то каким, какая связь существует между различными явлениями, наблюдается ли существование или последовательность, и каких именно явлений¹³.

Таблица может составляться учащимися по ходу наблюдения, когда результаты записываются в том порядке, в котором они поступают. Эта первичная таблица может дать некоторое представление о связях, общих чертах и различиях получаемых данных.

Приведем примеры.

Задание. Вспомним главных героев мультфильма «Алеша Попович и Тугарин змей». Богатырский конь Юлий и Алеша оказались у камня, указывающего три дороги: они не могут решить куда идти. Тогда они решили, что их судьбу определит случай. Юлий и Алеша по очереди подбрасывают по две монеты. Если обе монеты упадут гербами вверх, то выигрывает Юлий, если одна монета упадёт вверх гербом, а вторая – решкой, то выигрывает Алеша, а если обе монеты упадут решками вверх, то – ничья. Для того чтобы выяснить, справедлива ли эта игра, сыграй в неё 20 партий со своим одноклассником. При этом учащимся предлагают заполнить следующую таблицу:

Исход партии	Выиграл Юлий	Выиграл Алеша
Число исходов

Пользуясь таблицей, подсчитаем количество событий, при которых выигрывает Юлий, и количество событий, при которых выигрывает Алеша. Делаем выводы у кого же больше шансов выиграть.

Задание. Лев Алекс и зебра Марти подбрасывают 2 игральных кубика. Если сумма выпавших очков будет четной, выигрывает лев и друзья остаются жить в зоопарке. Если же сумма выпавших очков окажется нечетной, выигрывает зебра и друзья уходят из зоопарка на волю. Кубики решили подбросить 11 раз. У кого шансов выиграть больше?

Рассмотрим, как может происходить работа над заданием.

− Прочитайте задачу еще раз. Чем занимались лев Алекс и зебра Марти? (Они подбрасывали два игральных кубика и подсчитывали сумму выпавших очков.)

−Для чего они это делали? (Чтобы выявить победителя: льва Алекса или зебру Марти.)

− В каком случае победит лев Алекс? (Лев Алекс победит, если сумма выпавших очков будет четной.)

− При каких условиях победителем становится зебра Марти? (Победителем становится зебра Марти, если количество очков будет нечетным.)

− Что требуется узнать в задаче? (У кого больше шансов выиграть.)

− Чтобы ответить на вопрос задачи, что нам нужно знать? (Число событий, удовлетворяющих условиям, при которых выигрывает лев Алекс и зебра Марти.)

− Когда количество выигрышных вариантов будет известно, как узнаем, у кого больше шансов выиграть? (Шансов больше у того, у кого количество выигрышных вариантов будет больше.)

− Чему может равняться сумма выпавших очков? (Сумма выпавших очков может быть равной 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.)

− Почему мы не включаем единицу? (Так как подбрасывают два игральных кубика. На каждом кубике самое меньшее количество очков – 1. Если на каждом кубике выпадет по 1, их сумма будет равна 2. Значит, наименьшее количество очков в сумме равно 2, а 1 подбрасывая два игральных кубика получить нельзя.)

− Каким будет событие «сумма выпавших очков равна 1» достоверным или невозможным? (Событие «сумма выпавших очков равна 1» является невозможным.)

− Какие еще события невозможны при подбрасывании двух игральных кубиков? Почему? (Количество выпавших очков больше 12. Это событие невозможно, потому что 12 – это наибольшее количество очков, которые могут выпасть при подбрасывании двух игральных кубиков.)

− Подсчитаем количество событий, при которых выиграет лев Алекс. Какое условие должно выполняться? (Количество выпавших очков будет четным.)

− Какое количество очков удовлетворяет этому условию? (2, 4, 6, 8, 10, 12.)

− Подсчитаем количество способов, которыми можно получить четную сумму очков. Заполним таблицу на доске.

Сумма выпавших очков

2

4

6

8

10

12

Количество способов

1К

2К

1К

2К

1К

2К

1К

2К

1К

2К

1К

2К

1

1 и 1

1 и 3

1 и 5

2 и 6

4 и 6

6 и 6

2

2 и 2

2 и 4

3 и 5

5 и 5

3

3 и 1

3 и 3

4 и 4

6 и 4

4

4 и 2

5 и 3

5

5 и 1

6 и 2

− Какими могут быть варианты выпадения очков на кубиках, чтобы сумма была равна 2? (1 и 1.)

− Какие еще варианты могут быть? (Больше нет вариантов, этот вариант единственный.)

− Какое количество очков может выпасть на кубиках, чтобы сумма была равна 4? (1 и 3.)

− Это единственный способ? (Нет, еще могут быть варианты: 2 и 2, и 1.)

Рассуждая аналогично, заполняем остальные ячейки таблицы.

− Подсчитаем число событий, при которых выиграет лев Алекс. Чему оно равно? (Пользуясь таблицей, получаем ответ – 18.)

− Итак, существует 18 выигрышных комбинаций для льва Алекса. Подсчитаем количество событий, при которых победителем окажется зебра Марти. Какое условие должно выполняться? (Сумма выпавших очков должна быть нечетной.)

− Какие значения суммы удовлетворяют заданному условию? (3, 5, 7, 9, 11.)

Таблица заполняется аналогично предыдущей.

Сумма выпавших очков	3		5		7		9		11
Количество способов	1К	2К	1К	2К	1К	2К	1К	2К	1К	2К
1	1 и 2		1 и 4		1 и 6		3 и 6		5 и 6
2	2 и 1		2 и 3		2 и 5		4 и 5		6 и 5
3			3 и 2		3 и 4		5 и 4
4			4 и 1		4 и 3		6 и 3
5					5 и 2
6					6 и 1

− Пользуясь таблицей, подсчитаем количество событий, при которых выигрывает зебра Марти. Чему оно равно? (18 способов.)

− Итак, количество выигрышных комбинаций для зебры Марти равно 18, и для льва Алекса тоже 18. У кого же больше шансов выиграть? Почему? (Шансы на выигрыш у них равны, потому что количество выигрышных комбинаций равно.)

Ответ. Шансы равны.