
dopdf7
.pdf
δ(t)
b
a
t
Рис. 1.5. Імпульсне збурення
Величина імпульсного збурення характеризується площею, що обмежена амплітудним значенням імпульса.
Якщо площа дорівнює логічній одиниці, то збурення одиничне. Функція δ(t) називається дельта-функцією.
δ(t) = 0 → t ≠ 0 ,
(t)dt 1.
Перехідний процес, який виникає у системі в результаті імпульсного упливу називають імпульсною характеристикою.
Сигнал f(t), що упливає на динамічну систему, завжди може бути представлений у вигляді ряду Фур’є:
|
A |
|
k |
||
f (t) |
0 |
|
(Ak cosk t Bk sink t), |
||
|
|||||
|
2 |
k 1 |
|||
де А0 – амплітуда початкового упливу, |
|||||
|
|
|
|
k 1,2, , , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bk |
|
f (t)sin k tdt . |
||
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо амплітудно-частотна характеристика лінійної системи А(ω), а фазочастотна – φ(ω), то реакція х(t) на сигнал
N
f (t) Bk sin k t
k 1
матиме вигляд:
21
N
x(t) Bk A(k )sin[k t (k )],
k 1
де А(kω) – AЧХ на частоті ω; φ(kω) – ФЧХ на частоті ω. Ідеальні лінійні динамічні ланки при ω від 0 до ∞.
Реальні завжди мають нелінійності, які служать діапазоном пропускання. Частоту, що обмежує зверху область, при якій сигнали ще проходять,
називають частотою зрізу:
A ( |
|
|
|
|
|
|
Amax |
|
|
|||
|
) |
W(i |
|
|
) |
|
||||||
|
|
|
|
|||||||||
зр |
зр |
|
2 , |
|||||||||
y |
|
|
|
|
x |
|||||||
де Ay ( зр )– амплітуда коливань на вході, |
|
W(i зр) |
|
|
||||||||
|
|
– модуль АФХ об’єкта; ε – |
||||||||||
|
||||||||||||
зона нечутливості.
За відомою ωзр можна визначити величину інтервалу часу Δtmax між дискретними вимірюваннями.
Досліджуваний об’єкт представляють у вигляді структурної ланки, виділяють у ньому регулюючі і збурюючі упливи, а також вихідні величини та характер внутрішніх зв’язків.
х1 
 у1 х2
у1 х2
х3 |
у2 |
|
|
х4 |
у3 |
Рис. 1.6. Структурна схема з кількома вхідними упливами
 у1
у1
х 
 у2
у2
у3
Рис. 1.7. Структурна схема з одним вхідним упливом
Пунктиром позначені канали упливу вхідних параметрів на виході.
х1(t) → y1(t), y2(t), y3(t) х2(t) → y1(t), y2(t), y3(t) х3(t) → y1(t), y2(t), y3(t) х4(t) → y1(t), y2(t), y3(t)
Експериментальне дослідження статичних характеристик проводять за каналом x(t) → y(t). Переважно статичні залежності, визначені в достатньо широкому інтервалі зміни x(t), є нелінійними. Для визначення величин малих збурень x(t), при яких експериментальна статична характеристика y=f(t) відрізняється не більше, ніж на у від прямої лінії, необхідно проводити лінію
22

y = f(х) в області точок робочого режиму роботи (х0 ; у0).
При проведенні експерименту бажано використовувати давачі, передавальні функції яких близькі до одиниці в області низьких частот. Це означає, що в зоні пропускаючих об’єктами частот прилади повинні бути за своїми динамічними властивостями близькими до ідеальної ланки.
Пасивні методи побудовані на статичному аналізі властивостей об’єкта. Визначення характеристик при цьому зводиться до знаходження зв’язку між випадковими величинами і оцінювання правильності цього зв’язку. Величину, яка в результаті досліду може прийняти одне із ряду можливих значень і яку, знаючи умови досліду, неможливо передбачити наперед, називають випадковою. Найбільш загальними характеристиками випадкових процесів, які встановлюють їх ймовірнісні властивості, є закони розподілу. Закони розподілу можуть бути одномірними і багатомірними.
Нехай спостерігається реалізація x1(t), x2(t), … , x4(t) випадкової функції в m однакових процесах. Для деякого фіксованого моменту часу t=t1, випадкова функція характеризується значенням випадкових величин x1(t), ... , x4(t). Тоді функцію розподілу визначають ймовірністю того, що значення функції x(t) в момент часу t =t1 не перевищить деякої заданої величини х1. F1(x,t)=P[x(t)<x1].
Функція F1(x,t) не є спадною, яка зменшується до нуля при зменшенні х і до при зростанні х.
Якщо F1(x,t1) має похідну, то величину
f1 (x,t1 ) F(x,t1) називають одномірною густиною розподілу.
x
Якщо x(t1), x(t2) відносять до часу t1, t2 то ймовірність того, що x(t) буде не більше х1 при t=t1, і не більше х2 при t=t2, визначають двомірною функцією розподілу.
1.2.2. Математичні моделі механічних процесів
Сировинні транспортні потоки займають одне із центральних місць у ряді виробництв харчової промисловості, а необхідність раціонального керування ними є досить актуальною задачею. Потік може бути суцільним, розривним (перервним), періодично змінним відносно свого середнього значення або взагалі мати випадкові відхилення. Середня величина потоку матеріалів G(t) – це кількість матеріалу на конвеєрах, в трубопроводах.
Запас і утримуюча здатність характеризують накопичення матеріалу при виконанні певних оперецій і перед подаванням на наступну операцію.
Запас матеріалів допомагає компенсувати наслідки збурення в потоках. Припустимо, що в проміжній стадії виробничого циклу накопичено G(t)
матеріалу. Якщо витрата нового матеріалу що надходить – Gпост(t), а споживання із запасу – Gспож(t), то зростання запасу буде проходити при Gпост(t) > Gспож(t), а зменшення при Gпост(t) < Gспож(t).
Рівняння, що характеризує швидкість зміни запасу матеріалу:
23
dG(t)
dt G Gпост(t)
Gспож(t). |
(1.1) |
Залежність між текучим запасом G(t) і результуючою масовою швидкістю може бути отримана із рівняння (1.1):
G(t) [Gпост (t) Gспож (t)]dt Gdt.
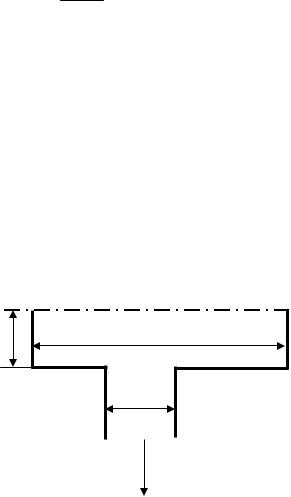
Найпростішим прикладом транспортних операцій є висипання сипучих матеріалів із отворів. Вивантаження матеріалу із ємності проходить через днище з випускними патрубками, до якого кріплять завантажувальний пристрій
– затвор або живильник.
Витрата сипучого матеріалу:
G = kDn
де D – діаметр отвору, k – коефіцієнт, який залежить від властивостей матеріалу, n – коефіцієнт, який залежить від форми отвору.
І |
І |
h |
Dбун |
D
ІІ  ІІ
ІІ
G
Рис. 1.8. Параметри для розрахунку
Незважаючи на те, що в зоні самого отвору і під ним сипучі тіла і рідини поводять себе однаково, різниця в поведінці сипучих тіл і рідин проє в зоні над отвором в ємності, причому чим вище над отвором, тим сильніше.
За аналогією з рідиною, використаємо рівняння Бернуллі для перерізів І-І і ІІ-ІІ (рис.1.8).
p |
1 |
|
2 |
p |
2 |
|
2 |
||
|
|
1 |
|
|
|
2 |
, |
||
1 |
|
2 |
|
||||||
|
2g |
|
2g |
||||||
де р1, р2 – псевдотиски або тиск на активний шар при основі ємності у відповідних перерізах; ρ1, ρ2, υ1, υ2, – густини і швидкості виходу штучного матеріалу, ξ – гідростатичні втрати на тертя.
Відомо, що статична густина матеріалу відрізняється від динамічної і її можна вважати змінною. Проте в момент початку руху статична густина переходить у динамічну, яка постійна для даного матеріалу і називається
критичною:
ρ1 = ρ2 = ρкр .
Тоді
υ1D2бун = υ2D2 .
24

за умови _Dбун > 3D→ G = F[2g ρкр(p1 – p2)].
Природа р1 із сипучими матеріалами відрізняється від природи тиску рідини (газу), тому вводять поняття “псевдотиску”. Його знаходять шляхом аналізу діючих сил у момент початку руху матеріалу.
Максимальне значення “псевдотиску” на дні ємності відповідає максимальному значенню горизонтальної сили, що діє на бічну поверхню, яка, в свою чергу, залежить від тангенса кута нахилу площини максимально зрізуючої напруги.
Для глибоких бункерів величина р1 стає незалежною від висоти насипного шару. Для круглих (квадратних) бункерів μ = μ’ отримаємо р1 = рmax при
h |
|
(3 5 2) |
, |
D |
h |
||
бун |
|
|
|
де μ – коефіцієнт внутрішнього тертя штучного матеріалу.
У зв’язку з тим, що частинки штучного матеріалу стають активними тільки в зоні над отвором, то “псевдотиски” на активний шар при основі ємності, обумовленої стовпцем частинок діаметром D і обмеженої зонами, для яких μ = μ’. Тоді р1 досягає максимального значення при
h (3 5 2)
D h
і становить
p1max hкрD 1 3 2 .
Витрата сипучого матеріалу
G h 2g 1 3 2 .
25
1.3.Типові ланки та їх характеристики. Поняття про передавальну функцію
До основних типових елементарних ланок як елементів САР, властивості яких дозволяють отримати динамічну характеристику системи, відносять:
-безінерційну нульового порядку (підсилююча);
-статичну першого порядку (аперіодична);
-статичну другого порядку (інерційна і коливна);
-астатичну першого порядку (інтегруюча);
-диференційну реальна;
-диференційну ідеальна;
-інтегродиференціюючу;
-ланку запізнення.
Елементарні ланки відрізняються порядком і характером диференціального рівняння (розглядаються ланки першого і другого порядку).
Таблиця 1.1. Безінерційна ланка нульового порядку (підсилювальна)
Рівняння |
Рівняння |
перехідного |
Передавальна |
Частотні |
ланки |
процесу |
|
функція |
характеристики |
|
|
|
|
W( j ) k |
y k x |
При t 0; |
y 0 |
W(p) k |
A( ) k |
При t 0; |
y(t) k |
( ) 0, приk 0 |
||
|
|
|
|
( ) , приk 0 |
Рівняння безінерційної ланки характеризується значенням коефіцієнта передавання k, який, як правило, називають коефіцієнтом підсилення. Дана ланка володіє властивістю статичності, коли у встановленому стані рівноваги (при цьому похідні вихідної величини дорівнюють нулю) існує однозначна залежність між значеннями вихідної і вхідної величин. Враховуючи, що час перехідного процесу дорівнюють нулю, безінерційна ланка нульового порядку є ідеалізованою, тому що в реальних ланках перехідний процес не може протікати миттєво.
Проте реальні ланки в окремих випадках описуванняють рівняннями нульового порядку, якщо тривалість їх перехідного процесу досить мала в порівнянні з тривалістю перехідних процесів інших ланок системи.
Якщо передавальний коефіцієнт ланки додатний, то фазовий зсув дорівнює нулю, якщо передавальний коефіцієнт від’ємний - фазовий зсув дорівнює (-π), тобто ланка є інерційною.
Важливою властивістю ланки нульового порядку є її здатність пропускати через себе вхідний сигнал без зміни його форми, а лише із зміною масштабу.
26
Логарифмічна амплітудна характеристика являє собою пряму, паралельну осі абсцис, яка проходить по відстані 20lgk, а ЛФЧХ показує відсутність фазового зсуву.
Таблиця 1.2. Статична ланка першого порядку (аперіодична)
Рівняння ланки |
Рівняння |
Передавальна |
Частотні |
|
перехідного |
||||
функція |
характеристики |
|||
|
процесу |
|||
|
|
|
|
|
|
|
|
|
|
|
|
W( j ) |
|
k |
|
|
|
|
dy |
|
t |
|
k |
Tj 1 |
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
k |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
W(p) Tp 1 |
|
|
|
||||||
T y k x |
y(t) k x(1 e T ) |
A( ) |
|
|
|
|
|
|||||||
|
|
|
|
|
||||||||||
1 ( t)2 |
|
|||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
||||
( ) arctg( T )
Рівняння статичної ланки першого порядку характеризується як коефіцієнтом передавання k, так і постійною часу ланки Т.
У зв’язку з тим, що перехідний процес протікає в часі, теоретично він дорівнює безкінечності, тому дана ланка є інерційною.
Перехідна функція представлена експоненціально, дотична до кривої перехідного процесу в довільній точці дорівнює значенню постійної часу
(рис.1.9).
h
T
k
0  t
t
Рис. 1.9. Перехідна характерисика аперіодичної ланки
Вигляд перехідної функції визначає аперіодичні властивості ланки. Ланка є релаксаційною, тому що швидкість зміни вихідної величини в початковий момент максимальна і далі зменшується, наближаючись до нуля, тобто уплив збурення поступово послаблюється. Ланка володіє властивістю самовирівнювання, тому сама прагне до нового встановленого стану і значення рівноваги вихідної величини. Власивість самовирівнювання визначають коефіцієнтом самовирівнювання :
1 . k
27
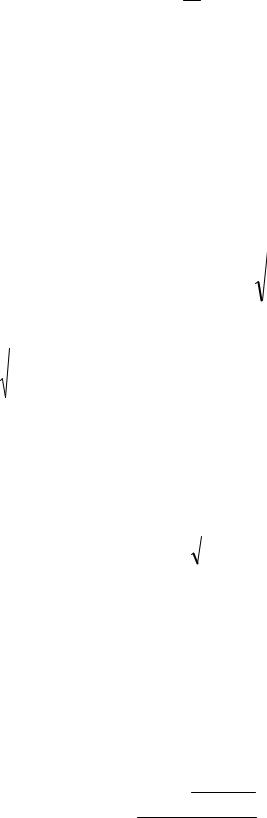
Частотні властивості ланки при k >0 характеризуються фазовим зсувом з
відставанням, яке змінюється від 0 до при зміні ω від 0 до +∞.
2
ЛАЧХ для ланки є сумою двох складових, перша із яких є постійна величина, що залежить від k. Тому форма ЛАЧХ для даної ланки не залежить від k. У зв’язку з цим для визначення виду характеристики, можна прийняти k=1 . При цьому перша складова дорівнює нулю.
При низьких частотах L(ω) ≈ 0, при високих L(ω) ≈ -20lgTω.
Таблиця 1.3. Статична ланка другого порядку
Рівняння ланки |
|
|
|
|
|
|
Рівняння перехідного процесу |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 d2 y |
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||
T1 |
|
|
|
T2 |
|
|
y k x |
|
|
|
y(t) k x [1 |
1 |
|
|
|
|
|
|
e t sin( t |
|||||||||||||
dt2 |
dt |
|
||||||||||||||||||||||||||||||
|
|
|
2 |
|||||||||||||||||||||||||||||
Корені: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
r j |
|
|
|
arctg |
)] |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
, |
1 |
1 ( |
T22 |
) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2T 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
T |
|
|
4T |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Передавальна функція |
|
|
|
Частотні характеристики |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W(j ) |
|
|
|
|
k |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T2(j )2 |
T j 1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|||||||
W(p) |
|
|
|
k |
|
|
|
|
|
|
|
A( ) |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
(1 2T12) 2T22 |
||||||||||||||||||||||||
T12p2 T2p 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) arctg ( |
|
|
T2 |
|
|
) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 T 2 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Статична ланка другого порядку (інерційна)
Така ланка містить дві постійних часу Т2 і Т1. При співведенняношенні: T22 4T12 0, характеристичне рівняння системи має дійсні корені, які отримуємо із виразу
r1,2 T2 
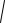 T22 4T12 .
T22 4T12 .
2T1
Перехідний процес має вигляд аперіодичної S-подібної кривої, яка являє спряження двох експоненціальних аперіодичних інерційних процесів, тобто дана ланка другого порядку може бути представлена як дві послідовно
28

ввімкнені аперіодичні ланки першого порядку. Аперіодичні затухаючі процеси мають різні знаки. Точка спряження двох аперіодичних процесів є точкою перетину кривої перехідного процесу або кривих розгону.
Статична ланка другого порядку (коливна).
При співведенняношенні T22 4T12 0 корені характеристичного рівняння будуть комплексними з від’ємною дійсною частиною і перехідний процес буде мати коливний затухаючий вигляд.
Постійні часу ланки зв’язані співведенняношенням
T2 ,
2T1
де ξ – коефіцієнт демпфування або декремент затухання.
Для замкненого перехідного коливного процесу 0<ξ<1; при ξ=0 корені чисто уявні й перехідний процес є коливним гармонічним (в такому випадку ланку називають консервативною); при ξ≥1 корені дійсні, рівні або нерівні, процес переходить в аперіодичний; при ξ<0 ланка постійна.
Постійна часу Т1 характеризує інерційність коливної ланки; Т2 – вказує характер затухання коливань.
Коливна ланка характеризується наявністю двох ємностей, що нагромаджують кінетичну або потенційну енергію і обмінюються ними.
При затухаючих коливаннях запас енергії, отриманий при збуренні, зменшується.
АФХ коливальної ланки характеризує фазовий зсув з відставанням на кут від 0 до (-π) при зміні частоти ω від 0 до +∞. Модуль АФХ змінюється від значення k (при одиничному вхідному збурені g=1) до деякого максимуму при резонансній частоті і далі зменшується до 0.
Резонансне значення модуля:
k A( )p 2 
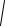 1 2 .
1 2 .
Резонансна частота:
1 2 2
p T .
ЛАЧХ і ЛФЧХ змінюють свій характер залежно від значення ξ. Затухання коливань практично можна оцінити двома методами:
- ступінь затухання, який виражається різницею двох сусідніх амплітуд одного знака у відсотках;
- логарифмічний декремент затухання у вигляді натурального логарифма відношення двох сусідніх амплітуд.
29

Таблиця 1.4. Астатична ланка першого порядку (інтегруюча)
|
|
|
Рівняння |
Передавальна |
Частотні |
|
||||||||||
Рівняння ланки |
перехідного |
|
||||||||||||||
|
|
|
процесу |
|
функція |
характеристики |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
W(j ) |
k |
; |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dy |
|
|
k |
|
t |
|
|
|
|
Tj |
|
||||
|
|
|
|
|
k |
|
|
k |
|
|
||||||
T |
k x |
y(t) |
|
xdt |
W(p) |
|
A( ) |
|
||||||||
|
dt |
|
T |
0 |
|
Tp |
|
T |
|
|||||||
|
|
|
|
|
|
|
|
|
|
( ) arctg( ) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
Із рівняння астатичної ланки бачимо, що в ній немає однозначної залежності між вхідною і вихідною величинами. Тут важливим є те, щоб швидкість зміни вихідної величини була пропорційна вхідній. Це випливає із характеру перехідної функції, де одному певному значенню вхідної величини відповідає множина значень вихідної величини. В цьому полягає астатизм.
Ланка є інтегруючою, тому що вихідна величина пропорційна інтеграла від вхідної величини.
В інтегруючій ланці немає самовирівнювання, тобто ρ=0.
Частотні властивості ланки такі, що ланка при всіх додатних частотах
створює постійне відставання по фазі на кут ( |
). АЧХ ланки має форму |
2 |
|
гіперболи. Амплітуда вихідної величини тим менша, чим більша частота. ЛАЧХ являє собою нахилену до осі частот пряму з нахилом 20 дБ або 6 дБ .
Диференціальні ланки можуть бути ідеальними і реальними. Ідеaльною ланкою є математична абстракція. В такій ланці в момент стрибкоподібного збурення на вході вихідна величина змінюється у вигляді миттєвого імпульсу нескінченно великої амплітуди при t=0 і падає до нуля при t ≠ 0. Імпульсна функція ідеальної диференціальної ланки подібна дельта функції.
Ланка створює постійне випередження по фазі на + 2 .
Реальну диференціюючу ланку можна навести у вигляді послідовного з’єднання статичної ланки першого порядку та ідеальної диференціюючої ланки.
Перехідна функція такої ланки може також починатися з миттєвого зростання вихідної величини, але на кінцеву величину, що визначається
відношенням kT . Чим менша постійна часу Т, тим більша вихідна величина в
ланці збурення на вході. Щоб запобігти різкій дії вихідного сигналу, слід збільшувати коефіцієнт передавання ланки.
30
