1.4. Економіко-математичні методи прогнозування збуту

Управління розвитком підприємства можна розглядати як циклічний процес, що складається із п'яти основних блоків:

— діагностичний аналіз, під час якого вивчається стан підприємства внаслідок впливу внутрішніх та зовнішніх, контрольованих та неконтрольованих чинників;

— підготовка, прийняття та реалізація ділових настанов, цілей діяльності;

— стратегічне планування, яке передбачає формування відповідно до намічених цілей ієрархії стратегій і побудову обґрунтованої системи прогнозів і довгострокових планів розвитку підприємства;

— тактичне планування, яке передбачає розробку та реалізацію оперативних дій;

— управлінський контроль, що включає збір та оцінку даних щодо діяльності підприємства, рішення про проведення ревізії знову діагностичного аналізу.

Реалізація стратегії розвитку підприємства передбачає побудову збалансованої системи прогнозів і планів на довго-, середньо- і короткострокову перспективу. Розвиток підприємства має бути прогнозованим і керованим. Персонал має знати, до яких цілей прагне підприємство, якими шляхами може відбуватися досягнення встановлених цілей, які завдання в загальній системі має виконувати кожен підрозділ і конкретний працівник [46, с. 618].

Прогноз – науково обґрунтоване судження про можливий стан об'єкта (підприємства) в майбутньому і (або) альтернативні шляхи і строки їх реалізації [9, с. 98].

Прогноз – являє собою спеціальне наукове судження конкретних перспектив розвитку якого-небудь явища [37, с. 187]

Прогноз – це результат процесу прогнозування, виражений у текстовій, математичній, графічній або іншій формі судження про можливий стан об'єкта в майбутньому [39, с. 72]

Прогнозування розвитку підприємства – процес розробки прогнозів, що ґрунтується на наукових методах пізнання економічних явищ, наукове обґрунтування можливих якісних і кількісних змін стану підприємства в майбутньому, а також альтернативних способів і строків досягнення очікуваного стану.

Сучасні методи прогнозування дають можливість зробити прогноз будь-якого показника який має історію розвитку. На даний момент існує велика кількість методів які дають змогу передбачити розвиток певного показника у майбутньому. Наведемо декілька із них.

1. Методи експертних оцінок (Метод Дельфі)

Спосіб прогнозування та оцінки майбутніх результатів дій на основі прогнозів фахівців.

При застосуванні методу експертних оцінок проводиться опитування спеціальної групи експертів (5–7 осіб) з метою визначення певних змінних величин, необхідних для оцінки досліджуваного питання. До складу експертів слід включати людей з різними типами мислення – образне і словесно-логічне, що сприяє успішному розв'язанню проблеми.

Необхідною умовою ефективного застосування методів експертної оцінки є достатня обізнаність експерта з досліджуваної проблеми, високий рівень ерудиції, здатність його давати чіткі вичерпні відповіді. Крім того, експерт не повинен бути зацікавленим в тому чи іншому варіанті вирішення поставленої перед ним проблеми. Експерти підбираються за ознакою їх формального професійного статусу – посади, наукового ступеня, стажу роботи та ін. Такий підбір сприяє тому, що в число експертів потрапляють високопрофесійні, з великим практичним досвідом у даній галузі спеціалісти.

Метод експертних оцінок – це фактично метод прогнозування, основоположним критерієм якого є досягнення згоди серед усіх учасників експертної групи. Організаційно це виглядає так. Експерти, обізнані у взаємопов'язаних сферах діяльності, детально відповідають на питання анкети, пов'язаної з досліджуваною проблемою. Кожен з них фіксує свою думку про проблему, а потім повідомляє про відповідь своїм колегам. У випадку розбіжності його прогнозу з думкою інших, експерт зобов'язаний пояснити причину такої невідповідності. Далі процедура повторюється до тих пір, поки думки експертів не збіжаться. При цьому потрібно дотримуватися анонімності, що допомагає уникнути можливості групових роздумів над проблемною ситуацією.

Для оцінки узагальненої міри узгодженості думок по всім напрямкам (факторам, параметрам) використовується коефіцієнт конкордації W.

Коефіцієнт конкордації може приймати значення від 0 до 1. Якщо W = 1, то думки експертів співпадають, якщо W = 0, то думки неузгоджені.

Якщо значення коефіцієнта конкордації w невелике, спостерігається незначна узгодженість поглядів експертів. Причини тут можуть бути різні: або в досліджуваній сукупності експертів справді немає спільності поглядів, або серед сукупності експертів існують групи з великою узгодженістю поглядів, однак їхні узагальнені думки протилежні.

Отже, метод експертних оцінок відіграє важливу роль в економічних дослідженнях, особливо у проведенні стратегічного і функціонально-вартісного аналізу [9, с. 76-77].

2. Методи ковзного середнього

  Основним твердженням, що лежить в основі даного методу, є те, що більш точний прогноз можна отримати, якщо застосовувати останні спостереження, до того ж, чим „новіші” дані, тим їх вага для прогнозу повинна бути більшою.

    2.1. Прогнозування на основі простого ковзного середнього.

  Із групи методів ковзного середнього найпростішим є метод ковзного середнього по n вузлах. В цьому методі середнє фіксованого числа n останніх спостережень використовується для оцінки наступного значення у.

В загальному випадку ковзне середнє для n вузлів матиме вигляд:

(1.22)

Недоліком методу простого ковзного середнього є те, що при обрахунку прогнозного значення останнє спостереження має таку ж вагу, як і попередні. Це пояснюється тим, що вага всіх n останніх спостережень, що беруть участь у визначенні ковзного середнього рівна 1/n. В багатьох випадках останні дані можуть більше сказати про те, що відбудеться в майбутньому, ніж попередні.

2.2  Зважене ковзне середнє.

      В основі даного методу лежить гіпотеза про те, що більш нові дані важливіші за старіші. Цей метод є узагальненням методу простого ковзного середнього.

  Якщо при застосування простого методу ковзного середнього кожний вузол мав вагу 1/n, то, наприклад, при зважене середнє визначається за формулою:

Yt+1=a0Yt+ a1Yt-1+…+ an-1Yt-n-1 (1.23)

причому

Можна приймати значення  експертним шляхом або з використанням вкладки „Поиск решения” пакету прикладних програм Excel.

2.3 Експоненційне згладжування.

    Очевидно, що в методі зваженого ковзного середнього існує безліч способів задати значення вагових коефіцієнтів так, щоб їх сума була рівною 1.

    Один з таких методів називається експоненційним згладжуванням. За методом експонеційного згладжування  для будь-якого t ≥ 1  прогнозоване значення визначається за формулою:

Yt+1=aYt+(1-a)Yt (1.24)

де α - визначена константа (параметр згладжування), причому 0≤ α ≤1. Значення константи  визначає ваговий коефіцієнт, який має останнє спостереження при обрахуванні прогнозного значення на наступний період. Якщо значення α буде близьке до 1, то практично прогнозне значення Yt+1 буде повністю залежати від Yt.

    Якщо t=1, Y2визначається за формулою Y2=aY1+(1-a)Y1. В даній формулі Y1 являє собою початкове прогнозне значення у₁. Отже, щоб зробити прогноз методом експоненційного згладжування потрібно знати прогноз Y1. В деяких випадках за Y1 беруть середнє значення всіх доступних значень Y, або середнє декількох останніх спостережень.

    Значення α можна приймати експертним шляхом або з використанням вкладки „Поиск решения” пакету прикладних програм Excel [39, 86].

3. Метод кореляційно-регресійного аналізу

Кореляційні моделі є одними з найважливіших у групі економіко-статистичних моделей.

Побудова кореляційної моделі здійснюється в кілька етапів:

1. Постановка задачі.

2. Збір статистичних даних.

3. Визначення виду функції (рівняння регресії).

4. Визначення тісноти зв’язку.

5. Установлення чисельного значення параметрів рівняння регресії.

6. Висновок про адекватність моделі.

На постановці задачі вважається, що зв’язок між аргументами і результативним показником може існувати і характеризується функцією .

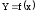Збір статистичних даних здійснюється на основі первинних документів, звітних даних. Деякі показники можуть бути отримані тільки після попередньої обробки зібраних даних.

Після збору даних здійснюється кореляційно-регресійний аналіз, що включає такі етапи:

1. Встановлення форми зв’язку між у та .

2. Визначення параметрів рівняння зв’язку (рівняння регресії).

3. Розрахунок параметрів тісноти зв’язку.

Розглянемо послідовність кожного етапу кореляційно-регресійного аналізу.

1. Установлення форми зв’язку. Для встановлення форми зв’язку між та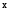будується кореляційне поле й по розташуванню точок на графіку обирається аналітичне рівняння зв’язку.

2. Визначення параметрів рівняння зв’язку. Визначити рівняння зв’язку (регресії) – значить, знайти його параметри. При цьому звичайно застосовують правило найменших квадратів (НМК), згідно з яким сума квадратів відхилень фактичних значень результативної ознаки (у) від його значень, знайдених за рівнянням регресії (у_х), має бути мінімальною:

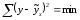(1.25)

За методом найменших квадратів параметри а₀ та а₁ знаходяться наступним чином:

, (1.26)

(1.27)

У цій функції за змінні приймаються послідовно а₀ та а₁. Екстремум функції двох змінних визначаються, якщо часткові похідні по цим змінним к 0.

, , (1.28)

(1.29)

(1.30)

Після перетворень останньої системи рівнянь, отримуємо систему нормальних рівнянь:

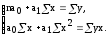(1.31)

Параметр а₀ рівняння регресії відображає усереднений вплив на результативну ознаку неврахованих (не виділених для дослідження) факторів.

Параметр називається коефіцієнтом регресії. У рівнянні прямої він показує, наскільки зміниться в середньому значення результативної ознаки при збільшенні факторної на одиницю.

3. Розрахунок показників тісноти зв’язку. Оцінка тісноти зв’язку між результативним і факторним ознаками здійснюється за допомогою спеціальних показників.

Для лінійної залежності застосовується лінійний коефіцієнт кореляції (або просто коефіцієнт кореляції). Для парного зв’язку він розраховується за формулою:

(1.32)

Коефіцієнт кореляції характеризує тісноту та напрям зв’язку, змінюється від -1 до +1. Якщо , то зв'язок між та функціональний; при – зв'язок відсутній; при – зв'язок прямий; при – зворотний.

Для якісної оцінки сили зв’язку можна скористатися шкалою Чеддока.

Таблиця 1.2 – Шкала сили зв’язку Чеддока

Тіснота зв’язку	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,99
Характеристика зв’язку	Слабкий	Помірний	Помітний	Високий (тісний)	Доволі високий (дуже високий)

Чим більше значення коефіцієнта кореляції тим тісніший зв'язок [12, с. 189-192].

4.1 Метод екстраполяції (трендового аналізу)

Термін «екстраполяція» має кілька тлумачень. У широкому значенні екстраполяція – метод наукового дослідження, що полягає в поширенні висновків, отриманих зі спостережень за однією частиною явища, на іншу його частину. У вузькому значенні - це визначення по ряду даних функції інших її значень поза цим рядом.

Екстраполяція полягає у вивченні сформованих у минулому і сьогоденні стійких тенденцій економічного розвитку і перенесення їх на майбутнє.

Мета такого прогнозу – показати, до яких результатів можна дійти в майбутньому, якщо рухатися до нього з тією самою швидкістю або прискоренням, що й у минулому.

Прогноз визначає очікувані варіанти економічного розвитку виходячи з гіпотези, що основні фактори і тенденції минулого періоду збережуться на період прогнозу або що можна обґрунтувати і врахувати напрямок їхніх змін у розглянутій перспективі.

Тренд являє собою тенденцію зміни певного показника в часі. 

Особливості прогнозування за трендом:

— прогнозування за трендом припустиме зі збереженням основної тенденції та умов розвитку і неприпустиме в разі настання стрибкоподібних, революційних змін;

— прогноз на основі трендів охоплює всі фактори в неявному й узагальненому вигляді (на відміну від багатофакторної регресійної моделі, де кожен фактор має числову характеристику міри свого власного впливу).

За даними ряду динаміки будується функція у = t(і), яка аналітично виражає залежність значень досліджуваної величини У від часу t і називається трендовою кривою або лінією тренда. Існує багато різних типів кривих, які використовуються на практиці як лінії тренда.

Рівняння тренда може бути описане такими залежностями:

а) лінійна:

y=a₀+a₁t (1.33)

б) степенева:

y=a₀t^a1 (1.34)

в) експоненціальна:

y=a₀e^t (1.35)

г) показникова:

y=a₀a₁^t (1.36)

д) логарифмічна:

y=a₀+a₁lnt (1.37)

де a₀, a₁  — константи;

t — порядковий номер періоду.

Після побудови кривої, лінію тренду перевіряють на адекватність за допомогою коефіцієнта детермінації.

Коефіцієнт детермінації (позначається як R² — R-квадра ) – це статистичний показник, що використовується в статистичних моделях як міра залежності варіації залежної змінної від варіації незалежних змінних. Вказує наскільки отримані спостереження підтверджують модель. Іншими словами, за допомогою коефіцієнта детермінації перевіряється модель на адекватність.

R² = 1 – (1.38)

де yі – значення у;

ŷ – теоретичне значення у, знайдене за рівнянням регресії;

ӯ – середнє значення у;

n – кількість спостережень.

Значення коефіцієнта детермінації змінюється від 0 до 1. Якщо значення цього показника ≥ 0,7 то модель є адекватною [29, с. 158-160].

Сьогодні науці відомо більше 150 методів і прийомів, які використовуються або запропоновані до використання у прогнозуванні. Кожен метод має свої особливості залежно від мети його використання і рівня проведених досліджень.

РОЗДІЛ 2 ОЦІНКА ТА АНАЛІЗ ЗБУТОВОЇ ДІЯЛЬНОСТІ ТОВ «БУЧАЦЬКИЙ СИРЗАВОД»