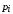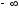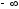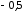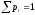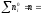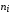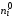рабочая тетрадь по МС
.docx
РАБОЧАЯ ТЕТРАДЬ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Заполнил (а) студент (ка) ___ группы ______факультета ветеринарной медицины и биотехнологии, специальности (направления подготовки)_________________________
___________________________ (Ф.И.О.)
Вариант № ____
Задание № 1. Группировка и статистический анализ выборки для случайной величины Х непрерывного типа.
Замечание. Случайная величина Х в «Математической статистике» называется чаще признаком Х генеральной совокупности.
Условие задания № 1. По выборке объёма n = __ исследуется случайная величина непрерывного типа Х – ________________________________________
____________________________________________________________________.
Выборочные данные помещены в таблицу 1 на следующей странице.
ТРЕБУЕТСЯ:
1. Сгруппировать выборочные данные в интервальный вариационный ряд частот. Изобразить вариационный ряд графически, построив гистограмму частот.
2. Вычислить по
сгруппированным данным точечные оценки
параметров распределения: выборочную
среднюю
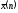 ,
выборочную дисперсию
,
выборочную дисперсию
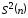 .
.
3. Проверить гипотезу
о нормальном распределении случайной
величины Х
на уровне значимости
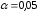 ,
применяя критерий согласия Пирсона.
,
применяя критерий согласия Пирсона.
Решение. Поместим исходные данные в таблицу 1:
Таблица 1.Исходные выборочные данные для случайной величины Х
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Для непрерывной
случайной величины Х
(для признака Х)
по результатам выборки составляется
интервальный вариационный ряд. Для
этого весь диапазон изменения выборочных
данных – размах вариации
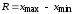 – накрывается совокупностью 5
– накрывается совокупностью 5 8
полузамкнутых интервалов
8
полузамкнутых интервалов
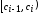 или
или
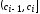 (по нашему произволу)
(по нашему произволу)
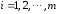 одинаковой длины h
так, чтобы значение
одинаковой длины h
так, чтобы значение
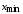 находилось приблизительно
посередине первого интервала, а значение
находилось приблизительно
посередине первого интервала, а значение
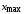 находилось в последнем интервале. Эту
длину рекомендуется вычислять по формуле
Террела-Скотта: h
находилось в последнем интервале. Эту
длину рекомендуется вычислять по формуле
Террела-Скотта: h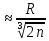 .
.
В нашей задаче
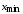 =_____,
=_____,
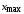 =_____,
n
= ___, поэтому, округляя результат вычислений
формулы Терелла-Скотта, возьмём h
= _____. Определяем левый конец первого
интервала
=_____,
n
= ___, поэтому, округляя результат вычислений
формулы Терелла-Скотта, возьмём h
= _____. Определяем левый конец первого
интервала
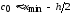 =
______________. Затем определяем границы
остальных интервалов
=
______________. Затем определяем границы
остальных интервалов
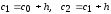 и т.д., пока значение
и т.д., пока значение
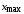 не окажется в интервале с номером
не окажется в интервале с номером
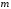 ,
являющимся последним. Для разнесения
данных из таблицы 1 по интервалам построим
таблицу 2, в которой определим частоты
,
являющимся последним. Для разнесения
данных из таблицы 1 по интервалам построим
таблицу 2, в которой определим частоты
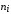 попадания выборочных данных в интервалы
(частота
попадания выборочных данных в интервалы
(частота
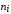 - это число значений признака Х,
попавших в интервал с номером
- это число значений признака Х,
попавших в интервал с номером
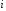 ).
Получим интервальный вариационный ряд
частот.
).
Получим интервальный вариационный ряд
частот.
Таблица 2
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Интервалы
|
|
|
|
|
|
|
|
|
Частоты
|
|
|
|
|
|
|
|
|
Относительные частоты
|
|
|
|
|
|
|
|
Количество
интервалов оказалось равным
т= ____. В
таблице 2 следует осуществить контроль
подсчёта частот:
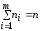 ,
где n
– объём выборки,
,
где n
– объём выборки,
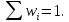
Если контроль оказался верным, переходим к следующим этапам работы, если же нет, то заполняем (исправляем) таблицу 2 повторно до выполнения контрольного равенства.
Графическим
изображением интервального вариационного
ряда, отражённого в таблице 2 служит
гистограмма
частот.
Построим гистограмму частот на рисунке
1. Для этого на оси абсцисс откладываем
отрезки, изображающие интервалы
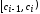 изменения значений случайной величины
Х
(признака Х).
На этих отрезках как на основаниях
строим прямоугольники с высотами,
равными частотам
изменения значений случайной величины
Х
(признака Х).
На этих отрезках как на основаниях
строим прямоугольники с высотами,
равными частотам
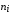 .
Полученная фигура и называется
гистограммой частот. Для наглядности
рекомендуется использовать всю плоскость
чертежа.
.
Полученная фигура и называется
гистограммой частот. Для наглядности
рекомендуется использовать всю плоскость
чертежа.
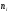
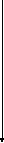
0


Рис. 1. Гистограмма частот интервального вариационного ряда.
2. Пусть случайная
величина Х
(признак Х)
имеет математическое ожидание М(X)= ,
дисперсию
,
дисперсию
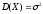 и среднеквадратичное отклонение
и среднеквадратичное отклонение
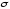 ,
при этом параметры
,
при этом параметры
 ,
,
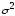 и
и
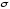 являются неизвестными. Очередной задачей
математической статистики является
точечная
оценка этих параметров. Для решения
этой задачи вычисляем середины интервалов
являются неизвестными. Очередной задачей
математической статистики является
точечная
оценка этих параметров. Для решения
этой задачи вычисляем середины интервалов
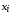 ,
придаем им соответствующие частоты
,
придаем им соответствующие частоты
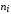 из интервального вариационного ряда
и преобразуем таблицу 2 в таблицу 3,
соединяя в ней интервальный вариационный
ряд частот( первая и третья строки) и
соответствующий ему дискретный
вариационный ряд частот ( вторая и третья
строки).
из интервального вариационного ряда
и преобразуем таблицу 2 в таблицу 3,
соединяя в ней интервальный вариационный
ряд частот( первая и третья строки) и
соответствующий ему дискретный
вариационный ряд частот ( вторая и третья
строки).
Таблица 3. Интервальный и соответствующий ему дискретный вариационный ряд частот для выборочных данных
|
Интервалы [ci-1, ci) |
|
|
|
|
|
|
|
|
|
Середины интервалов |
|
|
|
|
|
|
|
|
|
Частоты
|
|
|
|
|
|
|
|
|
По полученному
дискретному вариационному ряду частот
вычисляем точечные оценки неизвестных
параметров распределения признака
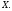
Несмещённой,
состоятельной и эффективной точечной
оценкой математического ожидания
 является выборочная
средняя
является выборочная
средняя
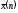 ,
которая вычисляется по формуле:
,
которая вычисляется по формуле:
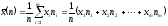 ,
,
где т равно числу интервалов. Для нашей задачи n = ___, т= ____. При этом рекомендуется ( во избежание слишком больших погрешностей округлений) в результатах промежуточных вычислений брать на 2 знака после занятой больше, чем у исходных данных. Вычисляем:
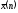 =
=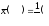
Обязательно следует
поместить значение
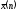 на ось абсцисс гистограммы ( на рис1.).
При этом следует помнить смысл
математического ожидания и его оценки
на ось абсцисс гистограммы ( на рис1.).
При этом следует помнить смысл
математического ожидания и его оценки
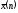 -
это среднее взвешенное значений признака
-
это среднее взвешенное значений признака
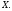 Посмотрите – является ли значение
Посмотрите – является ли значение
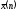 «центром тяжести» гистограммы? Если
уже визуально это не подтверждается,
то дальнейшие вычисления бессмысленны.
Рекомендуется этот этап вычислений
согласовать с преподавателем и только
после этого продолжать вычисления.
«центром тяжести» гистограммы? Если
уже визуально это не подтверждается,
то дальнейшие вычисления бессмысленны.
Рекомендуется этот этап вычислений
согласовать с преподавателем и только
после этого продолжать вычисления.
Выборочная
дисперсия
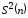 является состоятельной и эффективной,
но немного смещённой оценкой дисперсии
является состоятельной и эффективной,
но немного смещённой оценкой дисперсии
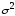 .
Впрочем, для больших выборок
.
Впрочем, для больших выборок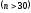 смещенность не играет роли.
смещенность не играет роли.
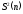 можно рассчитать
по одной из двух формул:
можно рассчитать
по одной из двух формул:
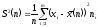 , (1)
, (1)
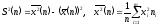 . (2)
. (2)
Для малых выборок
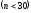 следует
пользоваться несмещённой эффективной
и состоятельной оценкой дисперсии
следует
пользоваться несмещённой эффективной
и состоятельной оценкой дисперсии
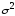 ,
каковой является исправленная
выборочная дисперсия
,
каковой является исправленная
выборочная дисперсия
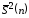 ,
связанная с выборочной дисперсией
,
связанная с выборочной дисперсией
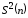 следующим образом:
следующим образом:
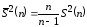 . (3)
. (3)
Несмещённой
эффективной и состоятельной оценкой
среднеквадратичного отклонения
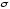 является исправленное
выборочное среднеквадратичное отклонение
является исправленное
выборочное среднеквадратичное отклонение
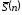 как квадратный корень из исправленной
выборочной дисперсии:
как квадратный корень из исправленной
выборочной дисперсии:
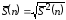 . (4)
. (4)
Рассчитываем выборочную дисперсию по формуле (2), вычисляя предварительно средний квадрат:
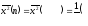

Для
визуального контроля следует учитывать
правило трех сигм нормального
распределения, т.е практически вся
гистограмма должна укладываться в
окрестности
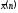 радиуса трех
радиуса трех
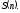 Проверьте это на рис.1.
Проверьте это на рис.1.
Итак, найдены
оценки математического ожидания
 ,
дисперсии
,
дисперсии
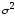 и среднеквадратичного отклонения
и среднеквадратичного отклонения
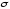 :
:
Таблица 4.
|
|
|
|
3. Если через
середины верхних оснований прямоугольников
гистограммы провести плавную линию, то
получим графический аналог плотности
вероятности признака
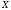 .
Далее на уровне значимости
.
Далее на уровне значимости
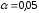 проверим гипотезу о том, что генеральная
совокупность распределена по нормальному
закону.
проверим гипотезу о том, что генеральная
совокупность распределена по нормальному
закону.
Будем опираться
на результаты группировки выборочных
данных из пункта 2, которые отражены в
таблице 3 и на рисунке 1. Проверка гипотезы
основана на сравнении эмпирических
(полученных ранее в таблице 3) частот
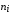 и так называемых теоретических
частот
и так называемых теоретических
частот
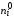 ,
которые рассчитываются в предположении
выполнения гипотезы о нормальном
распределении генеральной совокупности
с параметрами из таблицы 4:
,
которые рассчитываются в предположении
выполнения гипотезы о нормальном
распределении генеральной совокупности
с параметрами из таблицы 4:
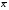 =
= _____,
_____,
 =
= _____. (5)
_____. (5)
Теоретические
частоты рассчитываются по формуле
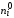 =
=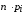 ,
где
,
где
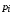 - вероятность попадания нормальной
случайной величины в интервал
- вероятность попадания нормальной
случайной величины в интервал
 ,
которая рассчитывается с помощью функции
Лапласа
,
которая рассчитывается с помощью функции
Лапласа
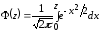 (см. таблицу ) по следующей формуле:
(см. таблицу ) по следующей формуле:
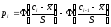 , (6)
, (6)
где
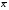 и
и
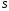 определяются выражениями (5). При этом
при вычислениях по формуле (6) левый
конец первого интервала следует
отодвинуть на минус бесконечность, а
правый конец последнего интервала
отодвинуть на плюс бесконечность,
полагая
определяются выражениями (5). При этом
при вычислениях по формуле (6) левый
конец первого интервала следует
отодвинуть на минус бесконечность, а
правый конец последнего интервала
отодвинуть на плюс бесконечность,
полагая
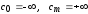 .
Процесс и результаты расчёта теоретических
частот заносятся в таблицу 5.
.
Процесс и результаты расчёта теоретических
частот заносятся в таблицу 5.
Таблица
5.Расчёт
теоретических частот
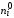 с помощью формулы (6).
с помощью формулы (6).
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|
|
|
|||
|
5 |
|
|
|
|
|
|
|
|
|||
|
6 |
|
|
|
|
|
|
|
|
|||
|
7 |
|
|
|
|
|
|
|
|
|||
|
8 |
|
|
|
|
|
|
|
|
|||
|
|
Контроль: |
|
|
||||||||
Замечание.
Левый конец первого интервала отодвинут
на минус бесконечность, т.е.
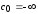 .
Не забудьте и правый конец последнего
интервала отодвинуть на плюс бесконечность,
полагая
.
Не забудьте и правый конец последнего
интервала отодвинуть на плюс бесконечность,
полагая
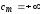 и учитывая, что
и учитывая, что
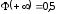 .
.
Соединим эмпирические частоты из таблицы 3 и теоретические частоты из таблицы 5 в следующей таблице 6. Таблица 6.Теоретические и эмпирические частоты для интервалов равной длины
|
Интервалы [ci-1, ci) |
|
|
|
|
|
|
|
|
|
Эмпирические частоты
|
|
|
|
|
|
|
|
|
|
Теоретические
частоты
|
|
|
|
|
|
|
|
|
На рисунке 1 была
изображена гистограмма частот, которые
теперь названы эмпирическими. Перенесём
эту гистограмму на рисунок 2 и построим
на этом же рисунке также гистограмму
теоретических частот, например, пунктирной
линией или линией другого цвета. На
рисунке 2 с данными из таблицы 7 качественно
видно насколько велико или мало
расхождение эмпирических и теоретических
частот.
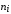 ,
,

0

Рис. 2. Гистограммы эмпирических (сплошная линия) и теоретических (пунктирная линия) частот интервального вариационного ряда.
Для количественной
оценки применим критерий согласия
Пирсона, подчиняющийся закону распределения
хи-квадрат с числом степеней свободы
k=m-l-1,
где l
– число параметров распределения (l=2
для нормального закона, т.е.
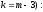
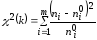 . (7)
. (7)
Необходимо учесть
следующее условие применимости критерия
Пирсона: малочисленные частоты (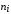 <5)
следует присоединить к частотам соседних
интервалов. В этом случае соответствующие
теоретические частоты также складывают,
а при определении числа степеней свободы
k=m-3
в качестве т
следует принять число групп (интервалов),
получившихся после объединения. Таким
образом, преобразуем таблицу 6 в таблицу
7.
<5)
следует присоединить к частотам соседних
интервалов. В этом случае соответствующие
теоретические частоты также складывают,
а при определении числа степеней свободы
k=m-3
в качестве т
следует принять число групп (интервалов),
получившихся после объединения. Таким
образом, преобразуем таблицу 6 в таблицу
7.
Таблица 7. Эмпирические и теоретические частоты после объединения
интервалов с малочисленными частотами
|
Эмпирические частоты |
|
|
|
|
|
|
|
Теоретические
частоты
|
|
|
|
|
|
|
Теперь по формуле (7) и по данным таблицы 7 вычисляем наблюдаемое значение критерия:
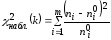 =
=
Итак,
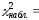 ______.
Далее по таблице распределения хи-квадрат
для числа степеней свободы k=m-3=____
и уровня значимости
______.
Далее по таблице распределения хи-квадрат
для числа степеней свободы k=m-3=____
и уровня значимости
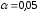 находим из условия
находим из условия
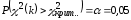 критическое значение критерия
критическое значение критерия
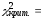 _____.
_____.
Поскольку
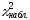 <
<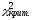 /
/
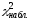 >
>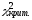 (ненужное зачеркнуть),
то гипотеза о том, что случайная величина
Х
распределена по нормальному закону,
принимается
/ отвергается
(ненужное зачеркнуть).
(ненужное зачеркнуть),
то гипотеза о том, что случайная величина
Х
распределена по нормальному закону,
принимается
/ отвергается
(ненужное зачеркнуть).
Задание № 2. Однофакторный дисперсионный анализ.
Условие задания № 2.
Таблица 8

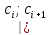
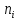
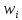
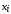
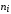
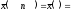
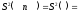
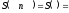
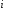
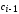
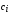
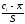
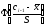
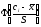
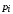
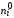 =n
=n