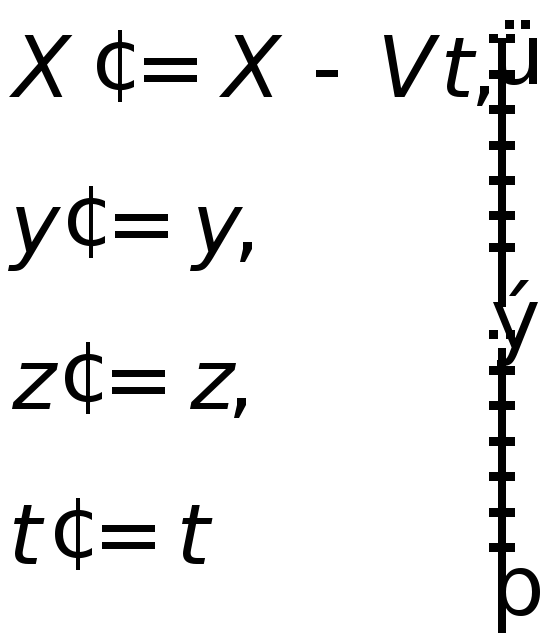- •Лекция 3.
- •2. Динамика материальной точки (поступательного движения твердого тела).
- •2.1. Первый закон Ньютона.
- •2.1.1. Инерциальные и неинерциальные системы отсчета.
- •2.1.2. Инертность тел. Масса.
- •2.1.3. Сила, Импульс силы.
- •2.2. Второй закон Ньютона.
- •2.2.1. Импульс материальной точки.
- •2.2.2. Формулировка второго закона Ньютона –основного закона динамики.
- •II закон Ньютона справедлив только для инерциальных систем отсчета!
- •2.2.3. Принцип независимости действия сил.
- •Если на материальную точку действует одновременно несколько сил, то каждая из них сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было.
- •2.3. Третий закон Ньютона.
- •2.3.1. Формулировка третьего закона Ньютона.
- •2.3.2. Силы инерции.
- •2.4. Преобразования Галилея.
- •Вопросы для самоконтроля.
- •Задачи для самостоятельного решения
- •Литература
2.3.1. Формулировка третьего закона Ньютона.
|
ЗАКОН ! |
“ Две взаимодействующие материальные точки действуют друг на друга с силами одной природы, которые численно равны и направлены в противоположные стороны вдоль прямой, соединяющие эти точки “.
|
Если
![]() - сила,
действующая на i-тую
материальную точку со стороны k-той
материальной точки, а
- сила,
действующая на i-тую
материальную точку со стороны k-той
материальной точки, а
![]() - сила,
действующая на k-тую
материальную точку со стороны i-той,
то согласно третьему закону Ньютона:
- сила,
действующая на k-тую
материальную точку со стороны i-той,
то согласно третьему закону Ньютона:
|
|
(2.6) |
Подчеркнем, что силы в третьем законе Ньютона:
приложены к разным материальным точкам;
в любой системе тел действуют парами;
имеют одну природу.
Сам третий закон применим только в рамках классической механики.
Силы
![]() и
и
![]() (приложенные
к разным материальным точкам) могут
взаимно уравновешиваться, только если
эти точки принадлежат к одному телу.
(приложенные
к разным материальным точкам) могут
взаимно уравновешиваться, только если
эти точки принадлежат к одному телу.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
Второй и третий законы Ньютона справедливы только для инерциальных систем отсчета!!!
2.3.2. Силы инерции.
В неинерциальных системах отсчета возникают силы инерции, которые вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как, если на какое-либо тело действует сила инерции, то нельзя указать со стороны какого тела она действует и, соответственно, не существует противодействующей силы. (Действие есть, а противодействия нет!).
2.4. Преобразования Галилея.
Галилей обратил внимание, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно, т.е. не привязав себя к другой инерциальной системе отсчета.
В основу классической механики положен принцип независимости пространства и времени. В качестве аксиом принимается абсолютность промежутков времени и длин:
|
|
1) промежуток времени между какими-либо двумя событиями одинаков во всех системах отсчёта; 2) размеры тела не зависят от скорости его движения относительно системы отсчёта.
Преобразованиями
Галилея
называются преобразования координат
и времени, применяемые в классической
механике при переходе от одной
инерциальной системы отсчёта
|
|
Рисунок 2.1 |
Если
сходные оси декартовых координат
инерциальных систем отсчёта
![]() и
и![]() проведены
попарно параллельно друг другу, и если
в начальный момент времени
проведены
попарно параллельно друг другу, и если
в начальный момент времени
![]() начала координат
начала координат![]() и
и![]() совпадают друг с другом (рис. 2.1), то
преобразования Галилея имеют вид:
совпадают друг с другом (рис. 2.1), то
преобразования Галилея имеют вид:
|
|
(2.7) |
или:
|
|
(2.8) |
где:
x,y,z
и
![]() ,
,![]() ,
,![]() - координаты точки М в системах отсчёта
- координаты точки М в системах отсчёта![]() в момент времениt
и
в момент времениt
и
![]() в момент времени
в момент времени![]() ;
;![]() и
и![]() - радиусы – векторы точки М в тех же
системах отсчёта;
- радиусы – векторы точки М в тех же
системах отсчёта;![]() ,
,![]() ,
,![]() - проекции скорости
- проекции скорости![]() системы
системы![]() на оси координат системы
на оси координат системы![]() .
.
|
|
Обычно
оси координат проводят так, что система
| |
|
|
| |
|
(2.9) | ||
|
Рисунок 2.2. | ||
Из
преобразований Галилея вытекает
следующий закон преобразования скорости
произвольной точки М (рис. 2.1.) при переходе
от одной инерциальной системы
![]() к другой
к другой![]() ,
,
|
|
(2.10) |
где
скорость точки М -
![]() в системе отсчета
в системе отсчета![]() ,
и
,
и![]() - в системе
- в системе![]() .
.
Соответственно преобразуются и проекции скорости на сходственные оси координат:
|
|
(2.11) |
Ускорение точки М в системах отсчёта
|
|
(2.12) |
одинаковы.
|
|
(2.13) |
Итак, ускорение материальной точки не зависит от выбора инерциальной системы отсчёта, т. е. инвариантно относительно преобразований Галилея.
Силы взаимодействия между материальными точками зависят только от их взаимного расположения и от скорости движения друг относительно друга.
Взаимное
расположение каких-либо двух точек 2 и
1, характеризуется вектором, равным
разности радиусов- векторов этих точек.
В системе
![]() вектором
вектором![]() ,
а в системе
,
а в системе![]() - вектором
- вектором![]() .
.
Согласно аксиоме 2 следует, что расстояния между точками 1 и 2 в системах одинаковы:
|
|
(2.14) |
или:
|
|
(2.15) |
Скорость движения точки 2 относительно точки 1 (относительная скорость) равна разности скоростей этих точек
|
В
системе
В
системе
|
(2.16) |
Из преобразований Галилея следует, что:
|
|
(2.17) |
Итак, взаимное расположение и скорость относительного движения двух любых материальных точек не зависят от выбора инерциальной системы отсчёта, т. е. они инвариантны относительно преобразований Галилея. Соответственно инвариантны и силы, действующие на материальную точку:
|
|
(2.18) |
Уравнения, выражающие законы Ньютона, инвариантны относительно преобразований Галилея, т. е. не изменяют свой вид при преобразовании координат и времени от одной инерциальной системы отсчёта к другой:
|
|
(2.19) |
где
![]() и
и![]() - масса рассматриваемой материальной
точки, одинаковая во всех системах
отсчёта.
- масса рассматриваемой материальной
точки, одинаковая во всех системах
отсчёта.
Т.о., в классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы механики одинаковы во всех инерциальных системах отсчёта.
Это значит, что в разных инерциальных системах отсчёта все механические процессы при одних и тех же условиях протекают одинаково.
Следовательно, с помощью любых механических экспериментов, проведённых в замкнутой системе тел, нельзя установить, покоится эта система или движется равномерно и прямолинейно (относительно какой-либо инерциальной системы отсчёта).
Механический принцип относительности означает, что в классической механике все инерциальные системы отсчёта совершенно равноправны.
Записанные
соотношения справедливы в случае
классической механики, т.е. u, ![]() << c.
<< c.
Для скоростей, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.