- •Интерференция световых волн
- •Интерференция от двух источников
- •Интерференция на тонких пластинах
- •Временная когерентность
- •Пространственная когерентность
- •Дифракция
- •Зоны Френеля
- •Дифракция Фраунгофера
- •Количественный критерий дифракции Френеля и дифракции Фраунгофера
- •Дифракционная решётка
- •Поляризация
- •Двойное лучепреломление
- •Искусственное двойное лучепреломление
- •Дисперсия
- •Элементарная теория дисперсии
- •Поглощение света
- •Рассеяние света
Дифракция Фраунгофера
|
|
Фраунгофер предложил иной способ наблюдения дифракции, получивший значительно большее практическое применение в оптике, поскольку приводит к более простым закономерностям (формулам). В этом способе на дифракционный объект (отверстие, щель и др) |
|
Рисунок 11 |
направляют параллельный пучок света (плоскую волну) и дифракционную картину наблюдают на достаточно большом расстоянии, т. е. практически в параллельных лучах (см. рис. 11). Это и есть дифракция Фраунгофера или дифракция в параллельных лучах.
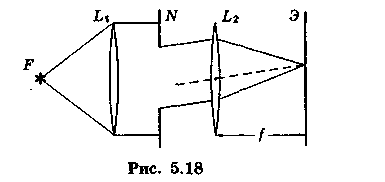
Точечный источник света располагают в фокусе F линзы L1. Из линзы выходит параллельный пучок лучей, на пути которого находится некоторая преграда N с отверстием. Дифрагированные лучи проходят линзу L2 и падают на экран Э, расположенный в фокальной плоскости линзы L2 (на фокусном расстоянии f). Таким образом, в каждую точку экрана падают только те лучи, которые до линзы L2 были параллельны друг другу.
|
|
Рассмотрим дифракцию на щели (см. рис.12). Разность хода волн, приходящих в точку Р от краев щели,
следовательно, в точку Р приходят волны от зон Френеля.
Если число
|
|
Рисунок 12 |
В общем случае
зависимость интенсивности света на
экране от угла
![]() дается формулой
дается формулой
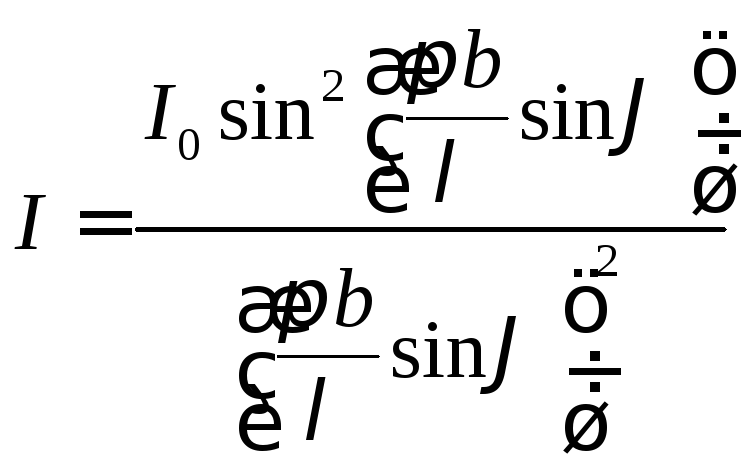 .
.
Количество минимумов
с одной стороны от центрального
![]() (т.к.
(т.к.![]() ).
Угловая ширина центрального максимума
).
Угловая ширина центрального максимума![]() .
.
Отметим также, что в середине симметричной дифракционной картины, состоящей из чередующихся светлых и темных полос, при дифракции Фраунгофера всегда образуется максимум освещенности (в отличие от френелевой дифракции, где центральная полоса может быть как светлой, так и темной).
Количественный критерий дифракции Френеля и дифракции Фраунгофера
Есть критерий, позволяющий судить, с каким видом дифракции — френелевой или фраунгоферовой — мы имеем дело в каждом конкретном случае. Чтобы его получить, воспользуемся формулой для радиусов зон Френеля, т. е.
![]()
Напомним, эта формула относится к случаю, когда на отверстие радиуса rт падает нормально плоская световая волна, причем т означает число зон Френеля, которые укладываются в данном отверстии для точки наблюдения Р, отстоящей от отверстия на расстояние b. Там же было отмечено, что характер дифракционной картины определяется только числом т открытых зон Френеля, и ничем другим. Значит, последнее выражение для т и можно взять в качестве интересующего нас параметра р, заменив в этом выражении rт на некоторый характерный размер h отверстия или преграды. Таким образом, безразмерный параметр ρ определяется следующим выражением
![]()
где h — некоторый характерный размер: радиус или диаметр (это не существенно) круглого отверстия, или, например, ширина щели и т. п.
Значение именно этого безразмерного параметра и определяет характер дифракции:
![]() «
1 — дифракция Фраунгофера,
«
1 — дифракция Фраунгофера,
![]() ~
1 — дифракция Френеля,
~
1 — дифракция Френеля,
![]() »
1
—
приближение геометрической оптики.
»
1
—
приближение геометрической оптики.