Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Приазовский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект лекций АиГ_ Реутова ИН_ Часть 2

.pdf

Скачиваний:

Добавлен:

05.03.2016

Размер:

828.8 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

ЛЕКЦИЯ 16.

ОПРЕДЕЛЕНИЕ ЦЕНТРА И ГЛАВНЫХ ОСЕЙ ЦЕНТРАЛЬНОЙ КРИВОЙ. ОТЫСКАНИЕ ВЕРШИНЫ И ОСИ ПАРАБОЛЫ.

Определение центра и главных осей центральной кривой.

Пусть дано уравнение кривой второго порядка

a x2 + 2a xy + a

y2 + 2a x + 2a y + a = 0.

(16.1)

Будем предполагать, что кривая не распадается, т.е. что

I3 = D ¹ 0. Найдем

собственные

значения l1 , l2

матрицы

æ a

соответствующие

им

è a12

a22 ø

собственные

векторы e1¢, e2¢.

Мы знаем, что в базисе,

образованном этими

векторами,

квадратичная

форма a

xy + a

приводится

каноническому виду l1 x¢2 + l2 y¢2 , а уравнение (16.1)

к виду

l1 x¢2 + l2 y¢2 + 2b1 x¢ + 2b2 y¢ + b = 0.

Собственные векторы e1¢,

e2¢ находятся, как известно, из систем уравнений

ì(a - l ) x + a y = 0,

ì(a - l

) x + a y

= 0,

12 1

(16.2)

+ (a22 - l2 ) y2 = 0,

ïa12 x1 + (a22 - l1 ) y1

= 0;

ïa12 x2

Поскольку

a11 - li

a12

= 0,

i = 1, 2,

- l

то каждая из систем (16.2) сводится к одному уравнению, например,

(a11 - l1 ) x1 + a12 y1 = 0

(для первой системы);

(a11 - l2 )x2 + a12 y2

= 0

(для второй системы).

Следовательно,

для

вектора

e1 = (x1; y1 )

имеем

l1 - a11

а для

a12

e2 = (x2 ; y2 )

l2 - a11

Таким образом,

угловые

коэффициенты новых

a12

осей координат в старой системе равны:

– для новой оси Ox,

соответствующей l1

k =

l1 - a11

(16.3)

a12

101

– для новой оси Oy, соответствующей l2

k2	=	l2 - a11	.	(16.4)

		a12

В дальнейшем достаточно, как мы видели, лишь переноса начала координат для того, чтобы уравнение кривой привелось к каноническому виду. Следовательно, k1 и k2 определяют направления главных осей кривой

(16.1).

Предположим, что мы рассматриваем центральную кривую второго порядка, т.е. что I2 = d ¹ 0. Для того чтобы найти центр кривой, т.е. начало

отсчета новой системы координат, воспользуемся следующими соображениями. Мы уже видели (доказательство теоремы 15.1), что если, не

меняя направления осей, перенести начало отсчета в точку(a; b ) т.е. если

положить

ìx = x¢ +a,

îy = y¢ + b,

то уравнение (16.1) приводится к виду:

a11 x

¢2

+ a22 y

¢2

(a12a + a22 b + a2 )+

+ 2a12 x y

+ 2x

(a11a + a12 b + a1 )+ 2 y

+(a11a 2 + 2a12ab + a22 b 2 + 2a1a + 2a2 b + a ) = 0.

Рассмотрим

систему

уравнений

ìa a + a

b + a

= 0,

(16.5)

îa12a + a22 b + a2 =

Т.к.

ее

главный

определитель

равенI

= d ¹ 0,

то

она

имеет

единственное решение (a; b ).

Если перенести начало координат в точку

(a; b ), то уравнении

кривой исчезнут слагаемые, содержащие члены с

первыми степенями, и значит, новое начало будет центром кривой.

Таким образом, центр центральной кривой второго порядка(эллипса

и гиперболы) находится из системы уравнений (16.5).

Отыскание вершины и оси параболы.

Рассмотрим

теперь

нецентральную

кривую

второго

(порядкапри

I2 = d = 0 ). Т.к. мы условились, что I3

= D ¹ 0,

то это парабола. Собственные

значения

æ a

пусть

будут l1 = 0 и l2

¹ 0. Направления

матрицы ç

è a12

a22 ø

102

новых

осей

определяются

по-прежнему. Для

новой

осиOx,

соответствующей l1

l1 - a11

= -

a11

(16.3)

a12

для новой оси Oy, соответствующей l2

l2 - a11

(16.4)

a12

Новое

начало

координат, .е.

вершину

параболы, можно

найти

следующим образом.

Для

параболы,

заданной

каноническим уравнением

y2 = 2 px,

ось

Oy служит касательной в вершине. Новая ось Oy в старых

координатах имеет угловой коэффициент k2

l2 - a11

Так как она служит

a12

касательной к параболе в ее вершине (a; b ),

то k2 = yx¢ (a; b ). Чтобы найти

уравнение(16.1) по

считая y функцией от x.

yx , продифференцируем

Получим:

+ a1

= 0,

2a11 x + 2a12 y + 2a12 xyx +

2a22 yyx

+ a2 yx

yx¢ = -

a11 x + a12 y + a1

a12 x + a22 y + a2

Следовательно, в вершине параболы

k2 = -

a11a + a12 b + a1

откуда:

a12a + a22 b + a2

(a11a + a12 b + a1 )+ k2 (a12a + a22 b + a2 ) = 0.

(16.5)

С другой стороны координаты вершины

параболы

удовлетворяю

уравнению кривой (16.1). Таким образом, координаты вершины параболы

можно найти, если решить систему уравнений:

ì(a x + a y + a )+ k

(a x + a

y + a

) = 0,

(16.6)

+ 2a xy + a y2 + 2a x + 2a y + a = 0.

ïa x2

Выясним

геометрический смысл

первого уравнения

(a11 x + a12 y + a1 )+ k2 (a12 x + a22 y + a2 ) = 0.

(16.7)

Это прямая, принадлежащая пучку, который определяется прямыми a11 x + a12 y + a1 = 0 и a12 x + a22 y + a2 = 0.

103

Угловые коэффициенты - a11 и - a12 этих прямых равны между собой.

a12 a22

Действительно, т.к. I

= d =

a11

a12

= 0,

то a a

= a 2

a11

a12

a22

a12

a22

Кроме того они равны k1 , следовательно, это прямые параллельны новой оси Ox. Значит, и принадлежащая этому пучку прямая(16.7) тоже параллельна новой оси Ox. Но так как она проходит через вершину, то можно сделать вывод, что уравнение (16.7) задает ось симметрии параболы.

N.	Привести	уравнение	2	2	+ 4x - 6 y +1	= 0	к
			кривойx - 2xy + y

каноническому виду. Найти для нее новую систему координат и построить график.

Решение.
I2		1		-1	= 0			кривая параболического типа.
I2	= d =	1		-1	= 0		Þ	кривая параболического типа.
		-1		1
I3 = D =		1		-1		2				данная кривая – парабола.
		1		-1		2
		-1		1		-3	= -1 ¹ 0 Þ
		2		-3		1
I1 = 2.
l	, l найдем из уравнения l2 - I l + I											2	= 0.
1	2									1		2
								l2 - 2l = 0; l = 0, l										2	= 2.
												1						2
Уравнение параболы имеет вид l y¢2 + 2b x¢																= 0,			где b = ±			-		D		.
Уравнение параболы имеет вид l y¢2 + 2b x¢																= 0,			где b = ±			-				.
										2			1						1					I1
																								I1
																									1
		1									¢2						¢				¢2						¢
		1		а уравнение параболы: 2 y											2x

b1	= ± -	2	;										±					=	0 или	y		= ±			2		x .
		2																							2
	Направления новых координатных осей:
				k1 =		-1	= 1	(ось Ox	¢	);			k2	=		2 -1			= -1	(ось Oy			¢		).

						-1										-1
						-1										-1

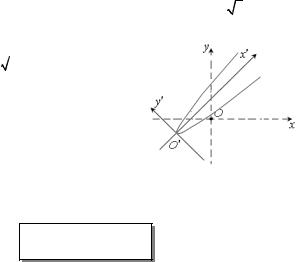
Уравнение оси параболы:

(x - y + 2)- (-x + y - 3) = 0,

x - y + 2, 5 = 0.

Найдем ось параболы:

104

			ì	31
ìx - y + 2,5 = 0,			ïx = -		,
			ïx = -	8	,
		Û	ï	8
í	= 0;	Û	í	11
îx2 - 2xy + y2 + 4x - 6 y +1	= 0;		ï	11
			ïy = -		.
			ïy = -	8	.
			î	8

Уравнение

новой

найдем

как

уравнение

прямой, проходящей

осиOy

через точку

; -

÷ перпендикулярно прямой x - y + 2, 5 = 0. Имеем:

y +

= -1ç x +

x + y +

= 0.

¢2

Выше

мы

наши

каноническое

уравнение

параболыy

= ±

x . Знак в

через x из

правой части определяется направлением оси

Ox . Выражая

уравнения кривой, получим:

y = x + 3 ±

2x + 8.

Следовательно,

кривая

расположена

области

x ³ -4,

т.е. справа от

оси

Oy .

Направив ось

Ox¢

вправо, мы должны будем

в каноническом уравнении параболы взять

знак «+», а, направив ось Ox¢

влево – знак

«–». График кривой изображен на рис. 16.1.

Рис.16.1

ЛЕКЦИЯ 17.

ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПОВЕРХОСТИ ВТОРОГО ПОРЯДКА.

В этой лекции речь пойдет только о приведении общего уравнени поверхности второго порядка к каноническому виду. Пусть в прямоугольной декартовой системе координат в пространстве задано уравнение

f (x, y, z) = a11 x2 + 2a12 xy + a22 y2 + 2a13 xz + 2a23 yz + a33 z 2 + 2a1 x + 2a2 y +

+2a3 z + a = 0.

(17.1)

Рассмотрим квадратичную форму от трех переменных:

105

a11 x2 + 2a12 xy + a22 y2 + 2a13 xz + 2a23 yz + a33 z2 .

(17.2)

В некотором ортонормированном базисе она приводится к сумме квадратов:

l1 x¢2 + l2 y¢2 + l3 z¢2 .

При этом уравнение (17.1) приводится к виду

l1 x¢2 + l2 y¢2 + l3 z¢2 + 2b1 x¢ + 2b2 y¢ + 2b3 z¢ + b = 0.

Здесь возможны три случая: все li отличны от нуля; одно из li равно нулю; два из li равны нулю.

1. Пусть l1l2l3 ¹ 0. Точно таким же образом, как и в случае кривой второго порядка, можно избавиться от членов первой степени:

l1 ç x¢ +

Сделав подстановку

x¢¢ =

+ l2 ç y¢ +

+ l3 ç z¢+

+ c = 0.

l1 ø

l2 ø

l3 ø

x¢ +

y¢¢ =

y¢ +

l1 ,

z¢¢ = z¢

т.е. выполнив некоторый параллельный перенос осей координат, мы получим уравнение

l1 x¢¢2 + l2 y¢¢2 + l3 z¢¢2 + c = 0.

Это – уравнение центральной поверхности второго порядка (новое начало координат является ее центром).

Будем считать, что c £ 0 (в противном случае умножим уравнение на -1 ). При c > 0 возможны следующие случаи:

1)l1 > 0, l2 > 0, l3 > 0 - эллипсоид;

2)l1 > 0, l2 > 0, l3 < 0 - однополостной гиперболоид;

3)l1 > 0, l2 < 0, l3 < 0 - двуполостной гиперболоид;

4)	l1 < 0, l2 < 0, l3 < 0 -			пустое	множество (его	так же	называют
«мнимым эллипсоидом»).
		Еслиc = 0	и все li одного знака, получаем точку («мнимый эллипс»);
при c = 0 и li разных знаков – конус.
	2.	Пусть	один из	коэффициентовli равен нулю; пусть, например,
l3	= 0.	Тогда,	соответствующим		переносом начала	координат	уравнение
поверхности можно привести к виду
			l1 x¢¢2 + l2 y¢¢2 + 2b3 z¢¢ + b = 0.				(17.3)

Здесь возможны случаи b3 = 0 и b3 ¹ 0.

Приb = 0 уравнение (17.3) имеет вид

l1 x¢¢2 + l2 y¢¢2 + b = 0.

106

Это – уравнение цилиндрической поверхности, вид которой определяется ее направляющей l1 x¢¢2 + l2 y¢¢2 + b = 0 в плоскостиOx¢¢y¢¢ (эллиптический

цилиндр, гиперболический цилиндр, пара пересекающихся плоскостей, одна прямая или пара «мнимых плоскостей», пересекающихся по вещественной прямой, пустое множество точек, или «мнимый эллиптический цилиндр»).

При b3 ¹ 0 уравнение (17.3) приводится к виду

l1 x¢¢2 + l2 y¢¢2 + 2b3 z¢¢ = 0.

Если

l1l2 > 0,

то

этоллиптический

параболоид,

при

l1l2 < 0 - гиперболический параболоид.

Пусть среди li

два равны нулю, пусть,

например,

l2 = l3

= 0.

Уравнение (17.1) приводится к виду

l1 x¢¢2 + 2b2 y¢ + 2b3 z¢ + b = 0.

(17.4)

Если b2

= b3 = 0,

то имеем

пару параллельных плоскостей, различных

при l1b < 0,

совпадающих при b = 0 и «мнимых» при l1b > 0.

Наконец, если хотя бы один из коэффициентовb2 , b3

уравнения (17.4)

отличен от нуля, положим

b2 y¢¢ + b3 z¢¢

b3 y¢¢ - b2 z¢¢

¢¢

= x ,

+ b2

что,

как

легко

проверить, отвечает

переходу

новому(тоже

ортонормированному) базису с матрицей перехода

.ç

÷.

+ b2

-b2

+ b2

При этом уравнение (17.4) преобразуется в

l1 x¢¢2 + 2b22 + b32 y¢¢ + b = 0,

а это последнее уравнение, так как b22 + b32 ¹ 0, посредством параллельного переноса начала координат преобразуется в

l1 x¢¢2 + 2b22 + b32 y¢¢¢ = 0.

Это параболический цилиндр.

107

Заметим, без доказательства, что, как и в случае кривой второго порядка,

при

преобразовании

уравнения

поверхности

второго

порядка

можно

использовать инварианты. Здесь это будут

= a + a

+ a ,

a11

a12

a11

a13

a22

a23

a12

a22

a13

a33

a23

a33

a11

a12

a13

a11

a12

a13

a12

a22

a13

= d =

= D =

a13

a23

a33

a13

a23

a33

Выражения

a11

a22

a33

a11

a12

a11

a13

a22

a23

K3 =

a12

a22

a13

a33

a23

a33

называются

семиивариантами

поверхности (17.1).

K2 и K3

являются

инвариантами поворота; в случае I3

= I4 = 0 семиивариант K3 будет также

инвариантом параллельного переноса. В

случае I2 = I3 = I4 = K3

= 0 инва-

риантом параллельного переноса, кроме K3

будет также семиивариант K2 .

Характеристическое уравнение матрицы квадратичной формы(17.2)

совпадает с уравнением

l3 - I l2 + I

l - I

= 0,

(17.5)

корни которого l1 , l2 , l3 вещественны.

Для

поверхности

второго

порядка, заданной

уравнением (17.1),

координаты центра симметрии определяются из системы уравнений:

ìa x + a y + a z + a = 0,

(17.6)

ía12 x + a22 y + a23 z + a2

= 0,

ïa x + a

y + a z

+ a

= 0.

Пусть(a, b,g ) - решение истемы (17.6). После параллельного переноса системы координат

ìx = x¢ +a,

íy = y¢ + b, ïîz = z¢ + g

уравнение (17.1) преобразуется к виду:

108

¢2

¢ ¢

+ a22 y

¢2

¢ ¢

f0 (x , y , z ) + a4 = a11 x

+ 2a12 x y

+ 2a13 x z

+ 2a23 y z

Здесь a4¢ = f (a, b,g ), где

+a33 z2 + a4¢ = 0.

(17.7)

f (x, y, z) -

левая часть уравнения (17.1).

Метод

определения

вида

расположения поверхности второго порядка

по ее общему уравнению(17.1) аналогичен методу, описанному для кривой

второго порядка.

1. Если I3

¹ 0, I4

¹ 0,

то сначала уравнение (17.1) при помощи параллельного

переноса преобразуется к виду (17.7), а затем при помощи поворота* – к виду

l1 x¢¢2 + l2 y¢¢2 + l3 z¢¢2 +

= 0.

(17.8)

В зависимости от знаковl ,

l ,

получается одна из следующих

поверхностей: эллипсоид, «мнимый эллипсоид», конус, «мнимый конус»,

однополостной или двуполостной гиперболоид.

2. Если

I3 = 0, I4 ¹ 0,

то выполняя

сначала поворот, а затем

параллельный

перенос системы координат, придем к уравнению вида

l1 x¢¢2 + l2 y¢¢2 ± 2

z¢¢ = 0.

(17.9)

зависимости

от

знаковl ,

получаем

либо

эллиптический

параболоид, либо гиперболический параболоид.

3. Если I3

= I4

= 0, I2 ¹ 0,

K3 ¹ 0,

то находя из системы(17.6) уравнение оси

симметрии

поверхности

совмещая

эту

ось

параллельным

переносом, а

, придем к уравнению вида

затем поворотом, с осью O z

l1 x¢¢2 + l2 y¢¢2 +

= 0.

(17.10)

В зависимости от знаковl1 , l2 ,

получаем

одну

из

следующих

поверхностей:

эллиптический

цилиндр,

«мнимый

эллиптический

цилиндр»,

две

мнимые

пересекающиеся

плоскости, гиперболический

цилиндр.

= I4

= I2 = 0, K3

4. Если

¹ 0,

то,

выполняя

сначала

поворот системы

координат,

затем

еще

один

поворот

около,

соответствующейоси

единственному оставшемуся квадрату, и

затем –

параллельный

перенос,

придем к уравнению

l1 x¢¢2 ± 2

y¢¢ = 0,

(17.11)

109

которое задает параболический цилиндр.

5. И наконец, если I3 = I4 = I2 = K3 = 0, то левая часть уравнения(17.1)

распадается на произведение линейных множителей, . . поверхность распадается на пару плоскостей (пересекающихся, параллельных, «мнимых параллельных» или совпадающих). Их уравнения находятся точно так же, как и уравнения прямых в соответствующем алгоритме для кривых второго порядка. При этом уравнение поверхности приводится к виду (17.10), если I2 ¹ 0, или к виду

l1 x¢¢2 +	K2	= 0,	(17.12)

	I1

если I2 = 0.

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

Соседние файлы в папке Лекции

#
05.03.20164.22 Mб11Конспект лекций АиГ_ Реутова ИН_ Часть 1.pdf
#
05.03.2016828.8 Кб13Конспект лекций АиГ_ Реутова ИН_ Часть 2.pdf