Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Приазовский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект лекций АиГ_ Реутова ИН_ Часть 2

.pdf

Скачиваний:

Добавлен:

05.03.2016

Размер:

828.8 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>

ЛЕКЦИЯ 12.

ПРИВЕДЕНИЕ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ МЕТОДОМ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ.

Lemma	Пусть	R - вещественное				евклидово		пространство		и
	T = (cij ) - матрица перехода					от	ортонормированного		базиса
	e = (e1 , e2 ,..., en )			к	другому		ортонормированному			базису
	e¢ = (e1¢, e2¢,..., en¢ ). Тогда T -1 = T T .
Доказательство.
Т.к.	T = (cij )	- матрица	перехода			от	базисаe к	¢	то
Т.к.	T = (cij )	- матрица	перехода			от	базисаe к	базису e ,	то
ei¢ = c1i e1 + c2i e2 +... + cni ei "i =				.
ei¢ = c1i e1 + c2i e2 +... + cni ei "i =			1; n	.
Рассмотрим		линейное	преобразованиеj				с матрицейT . Согласно
условию	леммы j		переводит			ортонормированный			базис	в
ортонормированный. Значит,			j -		ортогональный оператор. Тогда j* = j-1 ,
т.е. T * = T -1 , но T * = T T Þ T T = T -1 .
Пусть в евклидовом пространстве R						выбран ортонормированный базис
								n
e1 , e2 ,..., en	и	дана			билинейная		Bформа(x, y) = å aij xi y j ,		где
								i , j =1
n	n
x = åxi ei , y = å y j ej .
i =1	j =1

Рассмотрим линейное преобразование j с такой же матрицей A = (aij ) в

том же базисе e1 , e2 ,..., en .
Согласно (11.7) при переходе к		¢	¢	,..., e	¢	матрица
Согласно (11.7) при переходе к	новому базисуe , e			,..., e		матрица
билинейной формы перейдет в матрицу		1	2	n
билинейной формы перейдет в матрицу
B = T T	AT	¢ .
e®e¢	e®e
А матрица линейного преобразования j ,		согласно (7.3), в матрицу

A¢ = T -1¢ ATe ®e¢.

e®e

Согласно лемме T -1 = T T . Следовательно, матрица билинейной формы и матрица линейного оператора преобразовываются одинаково.

Таким образом, в евклидовом пространстве любой билинейной форме

соответствует вполне определенное линейное преобразование, имеющее ту же матрицу в произвольном ортонормированном базисе.

Если B(x, y) - симметричная билинейная , формато j - самосопряженный оператор. Но матрица самосопряженного оператора в некотором ортонормированном базисе e1 , e2 ,..., en имеет диагональный вид:

æl		0 ö
ç	1	÷
ç	O	÷,
ç	0	÷
è	0	ln ø

где ei - собственные		векторы этого оператора, а	li -	соответствующиеим
собственные значения.
В этом базисе билинейная форма приводится к виду
		B(x, y) = l 1 x1¢y1¢ + l 2 x2¢ y2¢ +... + l n xn¢ yn¢ ,					(12.1)
а соответсвующая квадратичная форма, следовательно,					приводится к
каноническому виду:		B(x, x) = l 1 x1¢2 + l 2 x2¢2 +... + l n xn¢2 .
		B(x, x) = l 1 x1¢2 + l 2 x2¢2 +... + l n xn¢2 .					(12.2)
Этот	метод	называетсяметодом ортогонального			преобразования
приведения квадратичной формы к каноническому виду.
N. Привести	квадратичную форму f (x, x) = 7x2 + 6x2 + 5x2 - 4x x						- 4x x . к
		1	2	3	1	2	2	3

каноническому виду методом ортогонального преобразования и найти канонический базис.

Решение.

Запишем матрицу заданной квадратичной формы:

	æ 7		-2	0	ö
A =	ç	-2	6	-2	÷
	ç				÷.
	ç	0	-2	5	÷
	è				ø

Найдем собственные значения матрицы A.

7 - l	-2	0
-2	6 - l	-2	= 0.
0	-2	5 - l

Решив, полученное уравнение, имеем l1 = 3, l2 = 6, l3 = 9.

Таким образом, канонический вид заданной квадратичной формы: f (x, x) = 3y12 + 6 y22 + 9 y32 .

Для отыскания канонического базиса найдем собственные векторы.

			ì4x - 2 y = 0,
Если l = 3,	то ( A - lE ) X = 0	Û	ï
Если l = 3,	то ( A - lE ) X = 0	Û	í-2x + 3y - 2z
			ï
			î-2 y + 2z = 0;
Фундаментальная система решений: f1			= (1; 2; 2).
			ìx - 2 y = 0,
Если l = 6,	то ( A - lE ) X = 0	Û	ï
Если l = 6,	то ( A - lE ) X = 0	Û	í-2x - 2z = 0,
			ï
			î-2 y - z = 0;
Фундаментальная система решений: f2			= (2;1; -2).
			ì-2x - 2 y = 0,
Если l = 9,	то ( A - lE ) X = 0	Û	ï
Если l = 9,	то ( A - lE ) X = 0	Û	í-2x - 3y - 2z

ïî-2 y - 4z = 0;

Фундаментальная система решений: f3 = (2; -2;1).

	ì	3y - 2z
	ïx =		,
		2
= 0, Û	ï

	íy = z,

ïïz Î R.

ìx = 2 y,

Û íy Î R, ïîz = -2 y.

ìx = 2z,

= 0, Û íy = -2z, ïîz Î R.

Векторы

f1 , f2 , f3

ортогональны,

т.к.

это

собственные

векторы,

соответствующие

различным

собственным

значениям. Нормируем

эту

систему векторов.

= 3.

e =

= æ

;

; e =

= æ

;

; -

; e =

æ 2

; -

;

ö.

3 3 3

è 3 3 3 ø

e1 , e2 , e3

- канонический базис.

N. Привести квадратичную форму f (x, x) = 3x2

+ 3x2

+ 4x x

- 2x x . к

каноническому виду методом ортогонального преобразования и найти канонический базис.

Решение.

Запишем матрицу заданной квадратичной формы:

	æ0		2	2 ö
A =	ç	2	3		÷
	ç			-1÷.
	ç	2	-1	3	÷
	è				ø

Найдем собственные значения матрицы A.

-l	2	2
2	3 - l	-1	= 0.
2	-1	3 - l

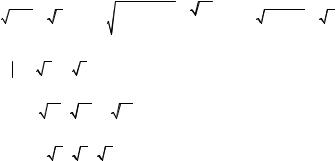
Решив, полученное уравнение, имеем l1,2 = 4, l3 = -2.

Таким образом, канонический вид заданной квадратичной формы: f (x, x) = 4 y12 + 4 y22 - 2 y32 .

Для отыскания канонического базиса найдем собственные векторы.

ì-4x + 2 y + 2z = 0,

ìx, y Î R,

Если l = 4, то ( A - lE ) X = 0 Û

- y

- z =

í2x

= 2x - y.

- y

- z =

îz

î2x

Фундаментальная система решений:

= (1; 0; 2),

= (0;1; -1).

ì2x + 2 y + 2z = 0,

ìx = -y - z,

Если l = -2,

то ( A - lE ) X = 0

= 0,

= z,

í2x + 5 y - z

íy

= 0;

Î R.

î2x - y + 5z

îz

Фундаментальная система решений:

= (-2;1;1).

Векторыf и f

, f

и f

ортогональны,

т.к. соответствуют различным

собственным значениям. Ортогонализируем систему векторов

f1 , f2 .

f1¢= f1 = (1;0; 2).

f2¢ = f2 +a f1¢

× f1¢

( f2 , f1 ) = ( f2 , f1 ) +a ( f1 , f1 ).

Найдем значение a,

при котором ( f2¢, f1¢) = 0.

¢ ¢

( f2 , f1¢)

0 +

0 - 2

( f2 , f1 )+a (

f1 , f1 ) = 0 Þ a = -

¢ ¢ = -

( f1 , f1 )

1+ 0 + 4 5

Тогда f ¢ = f

f ¢=

(0;1; -1)+

(1; 0; 2)

= æ

;1; -

ö.

è 5

f3¢ = f3 = (-2;1;1).

Нормируем систему векторов f1¢, f2¢, f3¢.

f1¢

f2¢

+1+

;

3¢

1+ 4

4 +1 +1

2 ö

; 0;

f1¢

f ¢

;

; -

канонический ортонормированный базис.

= ç

f2¢

3¢

;

= ç

ЛЕКЦИЯ 13.

ЗАКОН ИНЕРЦИИ КВАДРАТИЧНЫХ ФОРМ. ОПРЕДЕЛЕННЫЕ КВАДРАТИЧНЫЕ ФОРМЫ. КРИТЕРИЙ СИЛЬВЕСТРА.

Закон инерции квадратичных форм.

Приводя квадратичную форму к каноническому виду различными способами, мы, очевидно, будем получать различные коэффициенты. Однако справедливо следующее утверждение, которое носит название закона инерции квадратичных форм.

Th. 13.1

Если

квадратичная

форма приводится к сумме квадратов

двух

различных

базисах, то

число

положительных

коэффициентов и число отрицательных коэффициентов

обоих случаях одно и то же.

Доказательство.

базисеe , e ,..., e

квадратичная

форма

приводится

Пусть

каноническому виду:

A(x, x) = x2

+ x2

+... + x2

- x2

-... - x2

(13.1)

p +1

p+q

А в базисе e1¢, e2¢,..., en¢ она приводится к каноническому виду:

A(x, x) = x1¢2 + x2¢2 + ... + xk¢2 - xk¢2+1 -... - xk¢2+m .

(13.2)

Предположим,

что

p > k.

Рассмотрим R1 = L (e1 , e2 ,..., ep ) Ì R и

= L (ek¢+1 ,ek¢+2 ,..., en¢ ) Ì R.

Заметим, что

dim R1 = p и dim R2

= n - k.

dim R1 + dim R2 = p + n - k > n Þ R1 I R2

¹ Æ.

Пусть x ÎR1 I R2 (x ¹ 0).

Тогда,

т.к.

x ÎR1 ,

то x = a1e1 +a2e2 +... +a p ep

åai2

¹ 0

Поскольку

÷.

x ÎR2 ,

то x = b1ek¢+1 + b2ek¢+2 +... + bn-k en¢

åbi2

¹ 0

÷.

Из (13.1) для x

имеем A(x, x) = a 2

+a 2 +... +a 2

> 0.

Из

(13.2)

для

имеем A(x, x) = -b 2 - b

2 -... - b 2

£ 0

(неравенство

k +m

нестрогое, т.к. возможно, что

k + m < n ).

Получили

противоречие.

Следовательно

p £ k. Аналогичноможнопоказать,

что k £ p.

Значит, p = k.

Так же доказывается, что и

q = m

Определенные квадратичные формы. Критерий Сильвестра.

Def. Квадратичная форма A(x, x) называется положительно определенной,

если A(x, x) > 0 "x ¹ 0.

Def. Квадратичная форма A(x, x) называется отрицательно определенной,

если A(x, x) < 0

"x ¹ 0.

Def.

Квадратичная

форма A(x, x)

называется положительно

полуопределенной, если A(x, x) ³ 0

"x ¹ 0.

Def.

Квадратичная

форма A(x, x)

называется отрицательно

полуопределенной, если A(x, x) £ 0

"x ¹ 0.

N. Рассмотрим билинейную форму B(x, y) = (x, y). Тогда, соответствующая

ей

квадратичная

формаB(x, x) = (x, x) ,

является

положительно

определенной.

N. Рассмотрим квадратичную форму

f (x, x) = (x1 + x2 + x3 )2 - 2 (x2 - x3 )2 .

При x1

= 0, x2 = 1, x3

= -1 f (x, x) < 0.

А при

x1 = x2 = x3

= 1 f (x, x) > 0.

Значит,

f (x, x)

не является ни положительно определенной, ни отрицательно

определенной.

Очевидно,

что

положительно

определенная

квадратичная

форма

приводится к сумме квадратов с положительными коэффициентами,

отрицательно определенная форма– к сумме квадратов с отрицательными

коэффициентами. Сформулируем

критерий, который

позволит

выяснить,

является ли квадратичная форма положительно определенной, не сводя ее к

каноническому виду.

Th. 13.2

(критерий Сильвестра)

Для

того, чтобы

квадратичная

формаA(x, x)

была

положительно определена, необходимо и достаточно, чтобы

ее главные миноры Di > 0, где

D1 = a11 , D2

a11

a12

,..., Dn = det (aij .)

a21

a22

Доказательство (индукция по числу переменных).

1) Пусть n = 1. Тогда A(x, x) = a

x2 .

В этом случае тверждение теоремы

очевидно.

m-1

2) Пусть теорема справедлива для n = m -1,

т.е. для A(x, x) = å aij xi x j .

i, j =1

3) Докажем справедливость утверждения теоремы для n = m, т.е. для

A(x, x) = å aij xi x j .

i, j =1

Необходимость. Пусть A(x, x) > 0,				докажем, что Di > 0.
m-1	m -1
A(x, x) = å aij xi x j + 2åaim xi xm + amm xm2 .
i , j =1	i =1
14243
B ( x ,x )
B(x, x) > 0. Иначе, если		бы B(x, x) £ 0, то для x = (x1 ,..., xm , 0) A(x, x) £ 0, а
это не так.
По предположению		индукции D1 > 0, D2 > 0, ... , Dm -1 > 0.						Покажем,	что
Dm = det (aij ) > 0. Т.к. A(x, x) > 0,				то в некотором базисе она приводится к
каноническому виду		¢2		¢2		¢2	- ее матрица в этом
каноническому виду	A(x, x) = x1		+ x2		+ ... + xm . Пусть B		- ее матрица в этом
базисе, тогда det B = 1 > 0. Согласно (11.7):
			B = T T AT ,
где A - матрица квадратичной формы в старом базисе,							B - в новом базисе,
T - матрица перехода от старого базиса к новому.
	det B = det T T ×det A ×det T = det A×(det T )2 .							(13.3)
Поскольку det B > 0,	то det A = Dm > 0.
Достаточность.	Пусть			D1 > 0, D2		> 0, ... , Dm > 0. Докажем,			что
						m -1
A(x, x) > 0. Из предположения				индукцииB(x, x) = å aij xi xj				> 0. Значит, в
						i, j =1
некотором базисе она приводится к каноническому виду:
				¢2	¢2	¢2
		B(x, x) = x1			+ x2 +	... + xm -1.

Сделав соответствующую замену переменных и положив xm = xm¢ имеем:

¢2

¢ ¢

¢2

A(x, x) = x1

+ x2

+ ... + xm-1

+ 2 (b1m x1 xm

+ b2m x2 xm

+... + bm-1,m xm -1 xm )+ amm xm

¢2

= (x1

+ b1m xm )

+... + (xm-1 + bm-1,m xm )

+ bxm , где

b = anm - b1m

- b2m

-... - bm -1.

Положим:

"i = 1; m -1

yi = xi

+ bim xm

ym = xm¢ .

Получим A(x, x) = y12 + y22 +... + bym2 .

Если	B - матрица квадратичной формы в новом базисе,		то det B = b.
Согласно	(13.3) знаки det B и Dm = det A	совпадают,	т.е. b > 0.

Следовательно, A(x, x) > 0 .

Следствие (критерий отрицательно определенной формы).

Квадратичная форма A(x, x) отрицательно определена тогда и только

тогда, когда D1 < 0, D2

> 0, D3

< 0,... и т.д. То есть знаки главных миноров

чередуются, начиная со знака «минус».

Доказательство.

A(x, x)

отрицательно

определена

тогда

только , когдатогда

-A(x, x) = å (-aij )xi x j

положительно определена,

т.е. все главные миноры

i , j =1

матрицы

æ -a11

-a12

-a1n ö

...

A =

-a

...

-a

2n ÷

ç .

-an1

-a2n

...

-ann ø

были положительны. Отсюда имеем:

-a11 > 0 Û D1 = a11 < 0.

-a11

-a12

= a a - a a

> 0 Û D

> 0.

-a21

-a22

-a11

-a12

-a13

-a21

-a22

-a23

= -D3 > 0 Û D3 < 0.

-a31

-a32

-a33

И так далее. То есть знаки главных миноров чередуются, начиная со знака «минус» .

N. Определить, является ли квадратичная форма, заданная своей матрицей, положительно определенной или отрицательно определенной.

æ-4 0

2 ö

æ1 2 2 ö

æ 2

-1 2 ö

а)

B =

-4 2

;

б)

B =

-2

;

в)

B =

-1 1

-3

÷.

-6

-3

Решение.

а) D = -4 < 0; D			-4 0					-4	0	2
								-4	0	2
	2	=			=16 > 0; D	3	=	0 -4 2			= -64 < 0.
1	2		0	-4		3
			0	-4				2	2	-6
								2	2	-6

Значит, квадратичная форма отрицательно определена согласно следствию из критерия Сильвестра.

б) D = 1 > 0; D	2	=	1	2	= 2 > 0. Значит, квадратичная форма не является ни
1	2		2	6
			2	6
положительно определенной, ни отрицательно определенной.
в) D = 2 > 0; D			2 -1						2	-1	2


	2	=				= 1 > 0; D	3	=	-1 1 -3			= 1 > 0.
1	2		-1	1			3
			-1	1					2	-3	11
									2	-3	11

Значит, согласно критерию Сильвестра квадратичная форма является положительно определенной.

ЛЕКЦИЯ 14.

ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ КРИВОЙ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ.

Def. Пусть

на плоскости выбрана

прямоугольная

декартова

система

координат. Множество точек плоскости, координаты которых удовлетворяют

уравнению

x2 + 2a xy + a y2

+ 2a x + 2a y + a = 0,

(14.1)

называют кривой второго порядка.

Th. 14.1

Уравнение (14.1)

задает

либо

эллипс,

либо

гиперболу,

либо

параболу,

либо

пару

прямых, либо

точку,

либо

пустое

множество.

Доказательство.

Пусть e1 , e2

- орты координатных осей.

Первые три слагаемые уравнения (14.1) задают квадратичную форму

f (x, x) = a x2

+ 2a

xy + a

y2 .

(14.2)

В некотором ортонормированном базисе e1¢, e2¢

она имеет канонический вид:

f (x, x) = l1 x¢2 + l2 y¢2 ,

где

l1 , l2

собственные

числа

æ a

, а e1¢, e2¢

матрицыA = ç

соответствующие собственные векторы.

èa12

a22 ø

Пусть вектор e1¢

получается из вектора e1 поворотом на

уголj.

Тогда

e2¢

может быть получен из e2

одним из двух способов: 1) поворот на угол j

(рис. 14.1); 2) поворот на угол j и симметрия относительно начала отсчета

(рис. 14.2).

Рис. 14.1	Рис. 14.2
На рис. 14.2 вектор e2¢¢ = -e2¢ -	собственный вектор матрицыA,

соответствующий тому же собственному значению, что и векторe2¢. Действительно, пусть матрица A - матрица линейного оператораy и

y (e2¢ ) = l2e2¢. Тогда y (e2¢¢) = -y (e2¢ ) = -l2e2¢ = l2 e2¢¢.

Таким образом, можно считать, что новый базис получен из старого путем поворота на угол j, т.е.

e1¢ = cosje1 + sinje2 , e2¢ = -sinje1 + cosje2 .

Матрица перехода к новому базису имеет вид:

					Te®e¢ =		æ cosj		-sinj ö
					Te®e¢ =		ç		÷.
							è sin j		cosj ø
Обозначим	æ x ö	,	X	¢	=	æ x¢ ö			¢	т.е.
Обозначим	X = ç ÷	,	X		=	ç ÷.	Тогда X = Te®e¢ X ,			т.е.
	è y ø					è y¢ø
								¢	¢
						ìx = cosj x			- sin j y ,	(14.3)
						í		¢	¢	(14.3)
						îy = sin jx			+ cosj y .

Подставим(14.3) в уравнение(14.1), получим:

	l1 x¢2 + l2 y¢2 + 2b1 x¢+ 2b2 y¢ + b = 0.							(14.4)
Описанное	преобразование		координат				называетсяприведением		к
главным осям.				матрицыA,
l1 , l2 - собственные значения				матрицыA,			которые	находятся	из
уравнения:
	q(l) =	a11 - l	a	a12		= 0.
	q(l) =	a11 - l		a12		= 0.
		a		22	- l
		12		22
Т.к. матрица A симметрическая, то l Î R Þ l1l2 = q(0),								т.е.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>

Соседние файлы в папке Лекции

#
05.03.20164.22 Mб11Конспект лекций АиГ_ Реутова ИН_ Часть 1.pdf
#
05.03.2016828.8 Кб13Конспект лекций АиГ_ Реутова ИН_ Часть 2.pdf