Алгоритмы для графов

Если эвристическая функция h(n) никогда не переоценивает фактическую минимальную стоимость достижения цели (то есть является нижней оценкой фактической стоимости), то такая функция называется допустимой (англ. admissible).

Если эвристическая функция h(n) удовлетворяет условию

h(a) ≤ cost(a, b) + h(b),

где b — потомок a, то такая функция называется преемственной (англ. consistent).

Если f(n) = g(n) + h(n) — функция оценки, h(n) — преемственная функция, то функция f(n) является монотонно неубывающей вдоль любого исследуемого пути. Поэтому преемственные функции также называются монотонными (англ. monotonic).

Любая преемственная функция является допустимой, но не любая допустимая функция является преемственной.

Если h₁(n), h₂(n) — допустимые эвристические функции, и для любого узла n верно неравенство h₁(n) ≥ h₂(n), то h₁ является более информированной эвристикой, или доминирует над h₂.

Если для задачи существуют допустимые эвристики h₁ и h₂, то эвристика h(n) = max(h₁, h₂) является допустимой и доминирует над каждой из исходных эвристик^[1][2].

Сравнение эвристических функций

При сравнении допустимых эвристик имеют значение степень информированности и пространственная и временная сложность вычисления каждой из эвристик. Более информированные эвристики позволяют сократить количество развёртываемых узлов, хотя платой за это могут быть затраты времени на вычисление эвристики для каждого узла.

Эффективный коэффициент ветвления ( effective branching factor) — среднее число преемников узла в дереве перебора после применения эвристических методов отсечения. По эффективному коэффициенту ветвления можно судить о качестве используемой эвристической функции.

Идеальная эвристическая функция (например) всегда возвращает точные значения длины кратчайшего решения, поэтому дерево перебора содержит только оптимальные решения. Эффективный коэффициент ветвления идеальной эвристической функции близок к 1^[1].

Примеры задач поиска

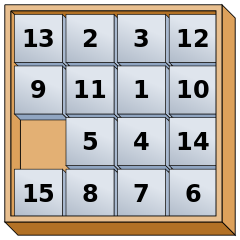
Сумма манхэттенских расстояний всех плиток от их целевых позиций: h_m(n)=3+0+0+3+2+4+2+4+1+3+2+2+ +3+3+2=34. Оптимальное решение состоит из 50 ходов.

В качестве моделей для испытания алгоритмов поиска и эвристических функций часто используются перестановочные головоломки — Пятнашки 3×3, 4×4, 5×5, 6×6, кубик Рубика,Ханойская башня с четырьмя стержнями.

В головоломке «Пятнашки» может быть применена эвристика h_m, основанная на манхэттенском расстоянии. Более конкретно, для каждой плитки подсчитывается манхэттенское расстояние между её текущим положением и её положением в начальном состоянии; полученные величины суммируются.

Можно показать, что эта эвристика является допустимой и преемственной: за один ход её значение не может измениться более чем на ±1.

Неинформированный поиск (также слепой поиск, метод грубой силы, англ. uninformed search, blind search, brute-force search) — стратегия поиска решений в пространстве состояний, в которой не используется дополнительная информация о состояниях, кроме той, которая представлена в определении задачи. Всё, на что способен метод неинформированного поиска, — вырабатывать преемников и отличать целевое состояние от нецелевого

Поиск в ширину (breadth-first search, BFS) — это стратегия поиска решений в пространстве состояний, в которой вначале развёртывается корневой узел, затем — все преемники корневого узла, после этого развёртываются преемники этих преемников и т.д. Прежде чем происходит развёртывание каких-либо узлов на следующем уровне, развёртываются все узлы на данной глубине в дереве поиска. Алгоритм является полным. Если все действия имеют одинаковую стоимость, поиск в ширину является оптимальным. Общее число выработанных узлов (временная сложность) равно O(bd+1), где b — коэффициент ветвления, d — глубина поиска. Пространственная сложность также равна O(bd+1)[1]. Реализация поиска в ширину может использовать очередь FIFO. В начале очередь содержит только корневой узел. На каждой итерации основного цикла, из начала очереди извлекается узел curr. Если узел curr является целевым, поиск останавливается, в противном случае узел curr развёртывается, и все его преемники добавляются в конец очереди

function BFS(v : Node) : Boolean;

begin

enqueue(v);

while queue is not empty do

begin

curr := dequeue();

if is_goal(curr) then

begin

BFS := true;

exit;

end;

mark(curr);

for next in successors(curr) do

if not marked(next) then

begin

enqueue(next);

end;

end;

BFS := false;

end;

Поиск в глубину (depth-first search, DFS) — стратегия поиска решений в пространстве состояний, при которой всегда развёртывается самый глубокий узел в текущей периферии дерева поиска. При поиске в глубину анализируется первый по списку преемник текущего узла, затем — его первый преемник и т. д. Развёрнутые узлы удаляются из периферии, поэтому в дальнейшем поиск «возобновляется» со следующего самого поверхностного узла, который всё ещё имеет неисследованных преемников

function DFS(v : Node; depth : Integer) : Boolean;

begin

if is_goal(v) then

begin

DFS := true;

exit;

end;

for next in successors(v) do

if DFS(next, depth + 1) then

begin

DFS := true;

exit;

end;

DFS := false;

end;

Поиск с ограничением глубины (depth-limited search, DLS) — вариант поиска в глубину, в котором применяется заранее определённый предел глубины l, что позволяет решить проблему бесконечного пути. Поиск с ограничением глубины не является полным, так как при l < d цель не будет найдена, и не является оптимальным при l > d. Его временная сложность равна O(bl), а пространственная сложность — O(b·l)[1][9]. Поиск с ограничением глубины применяется в алгоритме поиска с итеративным углублением.

function DLS(v : Node; depth, limit : Integer) : Boolean;

begin

if (depth < limit) then

begin

if is_goal(v) then

begin

DLS := true;

exit;

end;

for next in successors(v) do

begin

if DLS(next, depth + 1, limit) then

begin

DLS := true;

exit;

end;

end;

end;

DLS := false;

end;

Поиск в глубину с итеративным углублением (iterative-deepening depth-first search, IDDFS, DFID) — стратегия, которая позволяет найти наилучший предел глубины поиска DLS. Это достигается путём пошагового увеличения предела l до тех пор, пока не будет найдена цель. В поиске с итеративным углублением сочетаются преимущества поиска в глубину (пространственная сложность O(b·l)) и поиска в ширину (полнота и оптимальность при конечном b и неотрицательных весах рёбер). Хотя в поиске с итеративным углублением одни и те же состояния формируются несколько раз, большинство узлов находится на нижнем уровне дерева поиска, поэтому затратами времени на повторное развёртывание узлов обычно можно пренебречь. Временная сложность алгоритма имеет порядок O(bl)

function IDDFS(v : Node) : Integer;

var

lim: Integer;

begin

lim := 0;

while not DLS(v, 0, lim) do

lim := lim + 1;

IDDFS := lim;

end;

Поиск в глубину (англ. Depth-first search, DFS) — один из методов обхода графа. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» графа, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в нерассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из нерассмотренных вершин

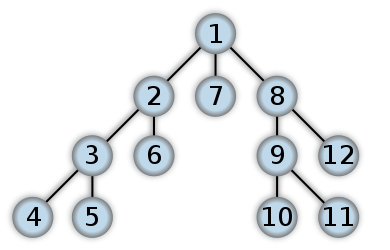
Пусть задан граф , где — множество вершин графа, — множество ребер графа. Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним следующие действия: Пройдём по всем вершинам . Если вершина белая, выполним для неё DFS(v). Процедура DFS (параметр — вершина ) Перекрашиваем вершину в серый цвет. Для всякой вершины , смежной с вершиной и окрашенной в белый цвет, рекурсивно выполняем процедуру DFS(w)[1]. Перекрашиваем вершину в чёрный цвет. Часто используют двухцветные метки — без серого, на 1-м шаге красят сразу в чёрный цвет. Нерекурсивные варианты На больших графах поиск в глубину серьёзно нагружает стек вызовов. Если есть риск переполнения стека, используют нерекурсивные варианты поиска. Первый вариант: можно сэмулировать стек вызова программно: для каждой из серых вершин в стеке будет храниться её номер и номер текущей смежной вершины . Процедура DFS (параметр — вершина ) Кладём на стек пару . Перекрашиваем вершину в серый цвет. Пока стек не пуст… Берём верхнюю пару , не извлекая её из стека. Находим вершину , смежную с и следующую за . Если таковой нет, извлекаем из стека, перекрашиваем вершину в чёрный цвет. В противном случае присваиваем , прямо в стеке. Если к тому же вершина белая, кладём на стек пару , перекрашиваем в серый цвет. Второй вариант: можно в каждой из «серых» вершин держать текущее и указатель на предыдущую (ту, из которой пришли). Третий вариант работает, если хватает двухцветных меток. Процедура DFS (параметр — вершина ) Кладём на стек вершину . Пока стек не пуст… Берём верхнюю вершину . Если она белая… Перекрашиваем её в чёрный цвет. Кладём в стек все смежные с белые вершины.

Поиск в ширину (англ. breadth-first search, BFS) — метод обхода графа и поиска пути в графе. Поиск в ширину является одним из неинформированных алгоритмов поиска[1]. Работа алгоритма Белый — вершина, которая еще не обнаружена. Серый — вершина, уже обнаруженная и добавленная в очередь. Черный — вершина, извлечённая из очереди[2] Поиск в ширину работает путём последовательного просмотра отдельных уровней графа, начиная с узла-источника . Рассмотрим все рёбра , выходящие из узла . Если очередной узел является целевым узлом, то поиск завершается; в противном случае узел добавляется в очередь. После того, как будут проверены все рёбра, выходящие из узла , из очереди извлекается следующий узел , и процесс повторяется. Неформальное описание Поместить узел, с которого начинается поиск, в изначально пустую очередь. Извлечь из начала очереди узел и пометить его как развёрнутый. Если узел является целевым узлом, то завершить поиск с результатом «успех». В противном случае, в конец очереди добавляются все преемники узла , которые ещё не развёрнуты и не находятся в очереди. Если очередь пуста, то все узлы связного графа были просмотрены, следовательно, целевой узел недостижим из начального; завершить поиск с результатом «неудача». Вернуться к п. 2. Формальное описание Ниже приведён псевдокод алгоритма для случая, когда необходимо лишь найти целевой узел. В зависимости от конкретного применения алгоритма, может потребоваться дополнительный код, обеспечивающий сохранение нужной информации (расстояние от начального узла, узел-родитель и т. п.) Рекурсивная формулировка:

BFS(start_node, goal_node) {

return BFS'({start_node}, ∅, goal_node);

}

BFS'(fringe, visited, goal_node) {

if(fringe == ∅) {

// Целевой узел не найден

return false;

}

if (goal_node ∈ fringe) {

return true;

}

return BFS'({child | x ∈ fringe, child ∈ expand(x)} \ visited, visited ∪ fringe, goal_node);

}

Итеративная формулировка:

BFS(start_node, goal_node) {

for(all nodes i) visited[i] = false; // изначально список посещённых узлов пуст

queue.push(start_node); // начиная с узла-источника

visited[start_node] = true;

while(! queue.empty() ) { // пока очередь не пуста

node = queue.pop(); // извлечь первый элемент в очереди

if(node == goal_node) {

return true; // проверить, не является ли текущий узел целевым

}

foreach(child in expand(node)) { // все преемники текущего узла, ...

if(visited[child] == false) { // ... которые ещё не были посещены ...

queue.push(child); // ... добавить в конец очереди...

visited[child] = true; // ... и пометить как посещённые

}

}

}

return false; // Целевой узел недостижим

}

Поиск «лучший — первый» (англ. best-first search) — это алгоритм поиска, который исследует граф путём расширения наиболее перспективных узлов, выбираемых в соответствии с указанным правилом. Джуда Перл (англ. Judea Pearl) описал поиск «лучший — первый», взяв в качестве оценки узла n значение некоторой «эвристической функции оценки f(n), которая, вообще говоря, может зависеть от природы n, описания цели, информации собранной поиском на данный момент и, самое главное, от каких-либо дополнительных знаний о предметной области». Некоторые авторы использовали поиск «лучший — первый» специально для описания поиска с эвристикой, служащей мерой близости к целевому состоянию, поэтому пути с лучшей эвристической оценку рассматриваются первыми. Этот специфический тип поиска называется жадным поиском «лучший — первый». Эффективный выбор текущего лучшего кандидата для продолжения поиска может быть реализован с помощью очереди с приоритетом. Алгоритм поиска A* (А-звездочка) является примером оптимального поиска «лучший — первый». Алгоритм «лучший — первый» часто используются для поиска пути в комбинаторном поиске.

OPEN = [Начальное состояние]

пока OPEN не пусто

повторять:

1. Удалить лучший узел из OPEN, назовем его N.

2. Если N целевое состояние, делаем трассировку пути назад к начальному узлу (через записи к родителям от N) и возвращаем путь.

3. Создать список потомков узла N.

4. Оцениваем каждого потомка, добавляем его в OPEN, и записываем N как его родителя.

закончить

В данной версии алгоритма не является полным, так как с его помощью не всегда ожно найти путь между двумя узлами, даже если он есть. Например, алгоритм «застревает» в цикле, если он заходит в тупик - узел с потомком, который является его родителем. Алгоритм вернётся к своему родителю, добавит тупиковой узел потомка в список OPEN и перейдёт на него ещё раз, и так далее.

Следующая версия расширяет алгоритм, используя дополнительные список CLOSE, содержащий все узлы, которые были оценены и не будут подлежать просмотру. Это позволяет избежать повторной оценки любого узла и не порождать бесконечные циклы.

OPEN = [исходное состояние]

CLOSE = []

пока OPEN не пусто

повторять:

1. Удалить лучший узел из OPEN, назовем его N, добавить его в CLOSE.

2. Если N целевое состояние, делаем трассировку пути назад к начальному узлу (через записи к родителям от N) и возвращаем путь.

3. Создать список потомков узла N.

4. Для каждого потомка повторять:

a. Если потомка нет в списке CLOSE: Оцениваем его, добавляем его в OPEN, и записываем N как его родителя.

b. Иначе: если это новый путь лучше, чем предыдущий, изменяем запись на родителя.

закончить

Поиск пути (англ. Pathfinding) — термин в информатике и искусственном интеллекте, который означает определение компьютерной программой наилучшего, оптимального маршрута между двумя точками.

В играх Поиск пути в контексте компьютерных игр касается пути, на котором движущийся объект ищет путь вокруг препятствий. Наиболее часто задача поиска пути возникает в стратегиях реального времени, в которых игрок даёт задание игровым юнитам (единицам) двигаться через игровой уровень, который содержит препятствия. Кроме стратегий, задача поиска пути, так или иначе, в той или иной мере встречается в большинстве современных игровых жанров. Так как игры становятся всё сложнее, то поиск пути также эволюционирует и развивается вместе с ними. Стратегии реального времени обычно содержат большие территории с открытым ландшафтом, в которых поиск пути обычно является простой задачей. Однако в большинстве случаев по карте перемещается не один юнит, а несколько, что создаёт потребность в различных и намного более сложных алгоритмах поиска пути для избежания пробок в узких областях игрового ландшафта. В стратегиях игровой уровень делится на тайлы (англ. tiles), которые действуют как узлы (англ. nodes) в алгоритме поиска пути. В жанре 3D-шутеров используются намного более ограниченные пространства, которые не так легко разделить на узлы. Здесь взамен узлов используются так называемые вэйпоинты (англ. waypoints; дословно — рус. точки пути). Вэйпоинты — это нерегулярные и вручную установленные узлы, которые содержат информацию о том, к каким другим узлам возможно добраться от данного.

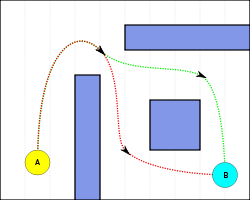
Эквивалентные пути между A и B в двухмерном пространстве

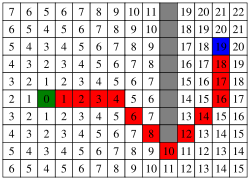
Пример A*-поискового алгоритма: зелёный: начальная точка красный: путь синий: пункт назначения

серый: препятствие

Алгоритмы По своей сути алгоритм поиска пути ищет на графе, начиная с одной (стартовой) точки и исследуя смежные узлы до тех пор, пока не будет достигнут узел назначения (конечный узел). Кроме того, в алгоритмы поиска пути в большинстве случаев заложена также цель найти самый короткий путь. Некоторые методы поиска на графе, такие как поиск в ширину, могут найти путь, если дано достаточно времени. Другие методы, которые «исследуют» граф, могут достичь точки назначения намного быстрее. Здесь можно привести аналогию с человеком, идущим через комнату. Человек может перед началом пути заранее исследовать все характеристики и препятствия в пространстве, вычислить оптимальный маршрут и только тогда начать непосредственное движение. В другом случае человек может сразу пойти в приблизительном или предполагаемом направлении цели и потом, уже во время пути, делать корректировки своего движения для избегания столкновений с препятствиями. К самым известным и популярным алгоритмам поиска пути относятся такие алгоритмы

• Алгоритм поиска A*

• Алгоритм Дейкстры

• Волновой алгоритм

• Маршрутные алгоритмы

• Навигационная сетка (Navmesh)

• Иерархические алгоритмы

• Обход препятствий

• Разделяй и властвуй

• Алгоритм поворота Креша