
Алгоритмы для графов
.docxАлгоритмы для графов
Алгоритм Беллмана–Форда — алгоритм поиска кратчайшего пути во взвешенном графе. За время O(|V| × |E|) алгоритм находит кратчайшие пути от одной вершины графа до всех остальных. В отличие от алгоритма Дейкстры, алгоритм Беллмана–Форда допускает рёбра с отрицательнымвесом. Предложен независимо Ричардом Беллманом и Лестером Фордом. Алгоритм маршрутизации RIP (алгоритм Беллмана–Форда) был впервые разработан в 1969 году, как основной для сети ARPANET.
Формулировка задачи Дан ориентированный или неориентированный граф G со взвешенными рёбрами. Длиной пути назовём сумму весов рёбер, входящих в этот путь. Требуется найти кратчайшие пути от выделенной вершины s до всех вершин графа. Заметим, что кратчайших путей может не существовать. Так, в графе, содержащем цикл с отрицательным суммарным весом, существует сколь угодно короткий путь от одной вершины этого цикла до другой (каждый обход цикла уменьшает длину пути). Цикл, сумма весов рёбер которого отрицательна, называется отрицательным циклом.
Решим поставленную задачу на графе, в котором заведомо нет отрицательных циклов. Для нахождения кратчайших путей от одной вершины до всех остальных, воспользуемся методом динамического программирования. Построим матрицу Aij, элементы которой будут обозначать следующее: Aij — это длина кратчайшего пути из s в i, содержащего не более j рёбер. Путь, содержащий 0 рёбер, существует только до вершины s. Таким образом, Ai0 равно 0 при i = s, и +∞ в противном случае. Теперь рассмотрим все пути из s в i, содержащие ровно j рёбер. Каждый такой путь есть путь из j-1 ребра, к которому добавлено последнее ребро. Если про пути длины j-1 все данные уже подсчитаны, то определить j-й столбец матрицы не составляет труда.
for
![]()
do
![]()
![]()
for
![]() to
to
![]()
do
for
![]()
if
![]()
then
![]()
return
![]()
Алгоритм Форда — Фалкерсона решает задачу нахождения максимального потока в транспортной сети. Идея алгоритма заключается в следующем. Изначально величине потока присваивается значение 0: f(u,v)=0 для всех u,v \in V. Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь.
Обнуляем все потоки. Остаточная сеть изначально совпадает с исходной сетью. В остаточной сети находим любой путь из источника в сток. Если такого пути нет, останавливаемся. Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток: На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью c_\min. Для каждого ребра на найденном пути увеличиваем поток на c_\min, а в противоположном ему — уменьшаем на c_\min. Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его. Возвращаемся на шаг 2. Важно, что алгоритм не конкретизирует, какой именно путь мы ищем на шаге 2 или как мы это делаем. По этой причине алгоритм гарантированно сходится только для целых пропускных способностей, но даже для них при больших значениях пропускных способностей он может работать очень долго. Если пропускные способности вещественны, алгоритм может работать бесконечно долго, не сходясь к оптимальному решению (см. пример ниже). Если искать не любой путь, а кратчайший, получится алгоритм Эдмондса — Карпа или алгоритм Диница. Эти алгоритмы сходятся для любых вещественных весов за время O(|V||E|^2) и O(|V|^2|E|) соответственно.
На каждом шаге алгоритм добавляет поток увеличивающего пути к уже имеющемуся потоку. Если пропускные способности всех рёбер — целые числа, легко доказать по индукции, что и потоки через все рёбра всегда будут целыми. Следовательно, на каждом шаге алгоритм увеличивает поток по крайней мере на единицу, следовательно, он сойдётся не более чем за O(f) шагов, где f — максимальный поток в графе. Можно выполнить каждый шаг за время O(E), где E — число рёбер в графе, тогда общее время работы алгоритма ограничено O(E*f). Если величина пропускной способности хотя бы одного из рёбер — иррациональное число, то алгоритм может работать бесконечно, даже не обязательно сходясь к правильному решению.
Пример дан ниже.
Пример не сходящегося алгоритма
Рассмотрим
приведённую справа сеть, с источником
![]() ,
стоком
,
стоком
![]() ,
пропускными способностями рёбер
,
пропускными способностями рёбер
![]() =
=
![]() ,
,
![]() =
=
![]() ,
,
![]() =
=
![]() и
пропускной способностью всех остальных
рёбер, равной целому числу
и
пропускной способностью всех остальных
рёбер, равной целому числу
![]() .
Константа
.
Константа
![]() выбрана
так, что
выбрана
так, что
![]() .
Мы используем пути из остаточного графа,
приведённые в таблице, причём
.
Мы используем пути из остаточного графа,
приведённые в таблице, причём
![]() ,
,
![]() и
и
![]() .
.
|
Шаг |
Найденный путь |
Добавленный поток |
Остаточные пропускные способности |
||
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
Заметим,
что после шага 1, как и после шага 5,
остаточные способности рёбер
![]() ,
,
![]() и
и
![]() имеют
форму
имеют
форму
![]() ,
,
![]() и
и
![]() ,
соответственно, для какого-то натурального
,
соответственно, для какого-то натурального
![]() .
Это значит, что мы можем использовать
увеличивающие пути
.
Это значит, что мы можем использовать
увеличивающие пути
![]() ,
,
![]() ,
,
![]() и
и
![]() бесконечно
много раз, и остаточные пропускные
способности этих рёбер всегда будут в
той же форме. Полный поток после шага 5
равен
бесконечно
много раз, и остаточные пропускные
способности этих рёбер всегда будут в
той же форме. Полный поток после шага 5
равен
![]() .
За бесконечное время полный поток
сойдётся к
.
За бесконечное время полный поток
сойдётся к
![]() ,
тогда как максимальный поток равен
,
тогда как максимальный поток равен
![]() .
Таким образом, алгоритм не только
работает бесконечно долго, но даже и не
сходится к оптимальному решению.
.
Таким образом, алгоритм не только
работает бесконечно долго, но даже и не
сходится к оптимальному решению.
Следующий пример показывает первые шаги алгоритма Форда — Фалкерсона в транспортной сети с четырьмя узлами, источником A и стоком D. Этот пример показывает худший случай. При использовании поиска в ширину алгоритму потребуется всего лишь 2 шага.
|
Путь |
Пропускная способность |
Результат |
|
|
Начальная транспортная сеть |
|
|
|
|
|
|
|
|
|
|
|
После 1998 шагов … |
|
|
|
Конечная сеть |
|
Поиск A* (произносится «А звезда» или «А стар», от англ. A star) — в информатике и математике, алгоритм поиска по первому наилучшему совпадению на графе, который находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной). Порядок обхода вершин определяется эвристической функцией «расстояние + стоимость» (обычно обозначаемой как f(x)). Эта функция — сумма двух других: функции стоимости достижения рассматриваемой вершины (x) из начальной (обычно обозначается как g(x) и может быть как эвристической, так и нет) и эвристической оценкой расстояния от рассматриваемой вершины к конечной (обозначается как h(x)). Функция h(x) должна быть допустимой эвристической оценкой, то есть не должна переоценивать расстояния к целевой вершине. Например, для задачи маршрутизации h(x) может представлять собой расстояние до цели по прямой линии, так как это физически наименьшее возможное расстояние между двумя точками. Этот алгоритм был впервые описан в 1968 году Питером Хартом, Нильсом Нильсоном и Бертрамом Рафаэлем. Это по сути было расширение алгоритма Дейкстры, созданного в 1959 году. Новый алгоритм достигал более высокой производительности (по времени) с помощью эвристики. В их работе он упоминается как «алгоритм A». Но так как он вычисляет лучший маршрут для заданной эвристики, он был назван A*. Обобщением для него является двунаправленный эвристический алгоритм поиска.
A* пошагово просматривает все пути, ведущие от начальной вершины в конечную, пока не найдёт минимальный. Как и все информированные алгоритмы поиска, он просматривает сначала те маршруты, которые «кажутся» ведущими к цели. От жадного алгоритма (который тоже является алгоритмом поиска по первому лучшему совпадению) его отличает то, что при выборе вершины он учитывает, помимо прочего, весь пройденный до неё путь (составляющая g(x) — это стоимость пути от начальной вершины, а не от предыдущей, как в жадном алгоритме). В начале работы просматриваются узлы, смежные с начальным; выбирается тот из них, который имеет минимальное значение f(x), после чего этот узел раскрывается. На каждом этапе алгоритм оперирует с множеством путей из начальной точки до всех ещё не раскрытых (листовых) вершин графа («множеством частных решений»), которое размещается в очереди с приоритетом. Приоритет пути определяется по значению f(x) = g(x) + h(x). Алгоритм продолжает свою работу до тех пор, пока значение f(x) целевой вершины не окажется меньшим, чем любое значение в очереди (либо пока всё дерево не будет просмотрено). Из множественных решений выбирается решение с наименьшей стоимостью. Чем меньше эвристика h(x), тем больше приоритет (поэтому для реализации очереди можно использовать сортирующие деревья). Псевдокод:
function A*(start,goal)
% множество уже пройденных вершин
var closed := the empty set
% множество частных решений
var q := make_queue(path(start))
while q is not empty
var p := remove_first(q)
var x := the last node of p
if x in closed
continue
if x = goal
return p
add x to closed
% добавляем смежные вершины
foreach y in successors(x)
enqueue(q, p, y)
return failure
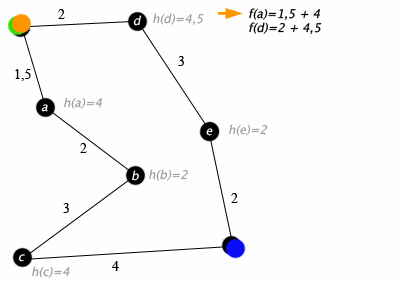 Примером
алгоритма A* в действии, где узлы – это
города, связанные дорогами и Н (х) является
самым коротким расстоянием до целевой
точки
Примером
алгоритма A* в действии, где узлы – это
города, связанные дорогами и Н (х) является
самым коротким расстоянием до целевой
точки
Как и алгоритм поиска в ширину, A* является полным в том смысле, что он всегда находит решение, если таковое существует. Если эвристическая функция h допустима, то есть никогда не переоценивает действительную минимальную стоимость достижения цели, то A* сам является допустимым (или оптимальным), также при условии, что мы не отсекаем пройденные вершины. Если же мы это делаем, то для оптимальности алгоритма требуется, чтобы h(x) была ещё и монотонной, или преемственной эвристикой. Свойство монотонности означает, что если существуют пути A—B—C и A—C (не обязательно через B), то оценка стоимости пути от A до C должна быть меньше либо равна сумме оценок путей A—B и B—C. (Монотонность также известна как неравенство треугольника: одна сторона треугольника не может быть длиннее, чем сумма двух других сторон.) Математически, для всех путей x, y (где y — потомок x) выполняется: g(x) + h(x) \le g(y) + h(y). A* также оптимально эффективен для заданной эвристики h. Это значит, что любой другой алгоритм исследует не меньше узлов, чем A* (за исключением случаев, когда существует несколько частных решений с одинаковой эвристикой, точно соответствующей стоимости оптимального пути). В то время как A* оптимален для «случайно» заданных графов, нет гарантии, что он сделает свою работу лучше, чем более простые, но и более информированные относительно проблемной области алгоритмы. Например, в неком лабиринте может потребоваться сначала идти по направлению от выхода, и только потом повернуть назад. В этом случае обследование вначале тех вершин, которые расположены ближе к выходу (по прямой дистанции), будет потерей времени.
Двунаправленный поиск пути в ширину (или глубину) — усложнённый алгоритм поиска в ширину (или глубину), идея которого заключается в формировании процесса поиска от начальной (прямой поиск) и от конечной вершины (обратный поиск) графа.
Идея Нахождение искомого пути сводится к определению путей от начальной к какой-то промежуточной, а от неё к конечной вершине. Реализуется проверкой в одном или обоих процессах, когда лист одного дерева поиска совпадёт с листом другого, после чего выделяются пути до этого элемента. Соединив пути получаем искомый путь. Если два поиска осуществляются параллельно — это ещё больше экономит время на получение искомого пути по сравнению с однонаправленным поиском. Преимущества и недостатки Повышенное быстродействие; Нужна память для хранения дерева поиска для того, чтобы можно было выполнить проверку принадлежности листа другому дереву.
Подсчёт количества операций Слишком зависит от конкретной ситуации, если поиск осуществляется не по n-арному дереву. Асимптотическая сложность возрастания количества операций Если известны единственные конкретные начальный и целевой элементы, то временная асимптотическая сложность прямого и обратного поисков равна , следовательно общая — + , что гораздо меньше чем . Пространственная асимптотическая сложность , вместо — у прямого, так как нужно хранить в памяти. Если известны конкретный начальный элемент и набор элементов, из которого один — целевой. Статистическая оценка Двунаправленный поиск, при заданных единственных начальном и конечном элементах, может улучшить однонаправленный поиск в ширину, обычно, в 2 раза. Наиболее сложным случаем для двунаправленного поиска является такая задача, в котором для проверки цели дано только неявное описание некоторого (возможно очень большого) множества целевых состояний, например всех состояний, соответствующих проверки цели «Мат» в шахматах. При обратном поиске потребовалось бы создать компактные описания всех состояний, которые позволяют поставить мат с помощью ходов и т. д. ; и эти описания нужно было бы сверять с состояниями, формируемыми при прямом поиске. Общего способа эффективного решения такой проблемы не существует. Алгоритм двунаправленного поиска Алгоритм состоит: прямого поиска, аналогичного одиночному поиску; обратного поиска; операции определения принадлежности листа другому дереву поиска.
Алгоритм Дейкстры (англ. Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его используют протоколы маршрутизации OSPF и IS-IS.
Формулировка задачи Примеры Вариант 1. Дана сеть автомобильных дорог, соединяющих города Московской области. Некоторые дороги односторонние. Найти кратчайшие пути от города Москва до каждого города области (если двигаться можно только по дорогам). Вариант 2. Имеется некоторое количество авиарейсов между городами мира, для каждого известна стоимость. Стоимость перелёта из A в B может быть не равна стоимости перелёта из B в A. Найти маршрут минимальной стоимости (возможно, с пересадками) от Копенгагена до Барнаула.
Задача о кратчайшем пути (англ. shortest path problem) — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов ребер, составляющих путь. Кратчайшая (простая) цепь часто называется геодезической [1]. Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для ее решения[⇨]. У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе. Значимость данной задачи определяется ее различными практическими применениями[⇨]. Например в GPS-навигаторах, где осуществляется поиск кратчайшего пути между двумя перекрестками. В качестве вершин выступают перекрестки, а дороги являются ребрами, которые лежат между ними. Сумма расстояний всех дорог между перекрестками должна быть минимальной, тогда найден самый короткий путь.
Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.
Граф
представляет собой совокупность
непустого множества вершин и ребер
(наборов пар вершин). Две вершины на
графе смежны, если они соединяются общим
ребром. Путь в неориентированном графе
представляет собой последовательность
вершин ![]() ,
таких что
,
таких что ![]() смежна
с
смежна
с ![]() для
для ![]() .
Такой путь
.
Такой путь ![]() называется
путем длиной
называется
путем длиной ![]() из
вершины
из
вершины ![]() в
в ![]() (
(![]() указывает
на номер вершины пути и не имеет никакого
отношения к нумерации вершин на графе).
указывает
на номер вершины пути и не имеет никакого
отношения к нумерации вершин на графе).
Пусть ![]() —
ребро соединяющее две вершины:
—
ребро соединяющее две вершины: ![]() и
и ![]() .
Дана весовая функция
.
Дана весовая функция ![]() ,
которая отображает ребра на их веса,
значения которых выражаются действительными
числами, и неориентированный граф
,
которая отображает ребра на их веса,
значения которых выражаются действительными
числами, и неориентированный граф ![]() .
Тогда кратчайшим путем из вершины
.
Тогда кратчайшим путем из вершины ![]() в
вершину
в
вершину ![]() будет
называться путь
будет
называться путь ![]() (где
(где ![]() и
и ![]() ),
который имеет минимальное значение
суммы
),
который имеет минимальное значение
суммы 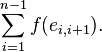 Если
все ребра в графе имеют единичный вес,
то задача сводится к определению
наименьшего количества обходимых ребер.
Если
все ребра в графе имеют единичный вес,
то задача сводится к определению
наименьшего количества обходимых ребер.
Существуют различные постановки задачи о кратчайшем пути:
-
Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
-
Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
-
Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.
В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объем затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).
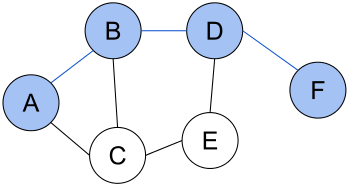
Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.
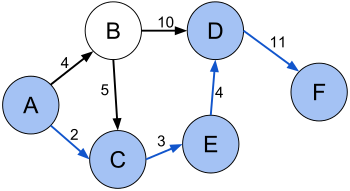
Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.
Информированный поиск (также эвристический поиск, англ. informed search, heuristic search) — стратегия поиска решений в пространстве состояний, в которой используются знания, относящиеся к конкретной задаче. Информированные методы обычно обеспечивают более эффективный поиск по сравнению с неинформированными методами. Информация о конкретной задаче формулируется в виде эвристической функции. Эвристическая функция на каждом шаге перебора оценивает альтернативы на основании дополнительной информации с целью принятия решения о том, в каком направлении следует продолжать перебор
В контексте поиска в пространстве состояний, эвристическая функция (англ. heuristic function) h(n) определена на узлах дерева перебора следующим образом:
h(n) = оценка стоимости наименее дорогостоящего пути от узла n до целевого узла.
Если n — целевой узел, то h(n) = 0.
Узел для развёртывания выбирается на основе функции оценки (англ. evaluation function)
f(n) = оценка стоимости наименее дорогостоящего пути решения, проходящего через узел n,
f(n) = g(n) + h(n),
где функция g(n) определяет стоимость уже пройденного пути от начального узла до узла n.
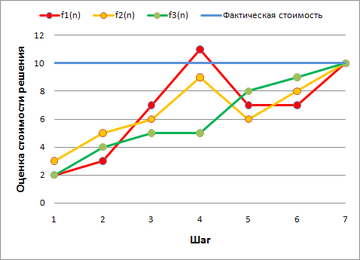
Значения функций вдоль оптимального решения f1(n) = g(n) + h1(n) — недопустимая эвристика f2(n) = g(n) + h2(n) — допустимая, но не преемственная f3(n) = g(n) + h3(n) — преемственная эвристика
