Розв'язок

1. Побудуємо кінематичну схему механізму в умовному масштабі (рис.5.2,а). На схемі покажемо задані сили 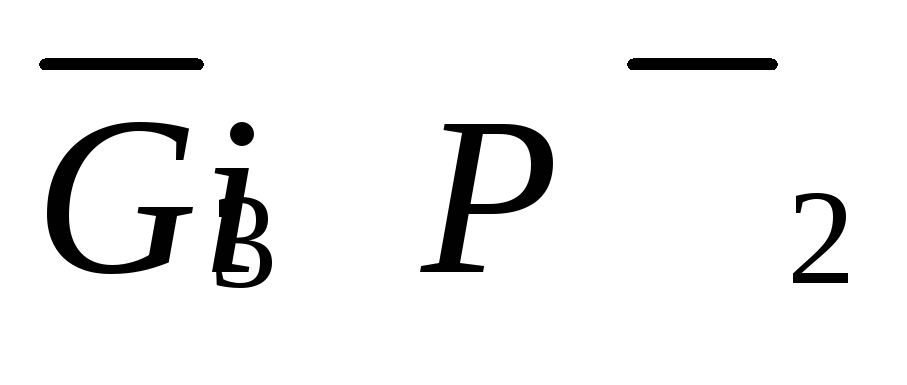, а також момент

М₃ , що діє на ланку 3. Урівноважуючий момент, який визначається, прикладемо (згідно умови) до ведучої ланки ОА, спрямувавши його у довільному напрямі. Силовий розрахунок механізму виконаємо без урахування сил і моментів сил інерції Даламбера.¹

Обидва запропоновані в умові методи розв’язку завдання потребують певних дій з силами. Тому при розгляданні рівноваги механізму або його окремих частин моменти сил, що прикладені до ланок, треба заміняти відповідними парами сил.

2. Визначення реакцій в кінематичних парах механізму і урівноважуючого моменту методом планів сил.

При розв’язку задачі методом планів сил, механізм умовно роз’єд-нують на структурні групи Ассура і механізм I-го класу. У нашому випадку маємо формулу будови механізму: I (0,1) → II (2,3).

Силовий розрахунок починають з кінця механізму. Для нашого механізму це означає, що спочатку треба розглянути рівновагу структурної групи (2,3), а за цим – рівновагу ведучої ланки 1. Зробимо ці кроки послідовно.

Рівновага структурної групи (2,3).

Побудуємо групу Ассура (2,3) в довільному масштабі (рис.5.2,б). Прикладемо до неї сили і. Момент М₃ заміняємо парою сил . Ці сили прикладемо на кінцях ланки 3 (в точках В і С), перпендикулярно до ланки 3 і у напрямі дії моменту М₃. Модулі сил пари дорівнюють:

Н (5.1)

В кінцевих шарнірах А і С прикладемо сили реакцій, що діють на ланки 2 і 3 з боку інших ланок механізму. В шарнірі А силу (сила, що діє на ланку 2 з боку ланки 1) розкладемо на складові: нормальнуі тангенціальну. В шарнірі С силу(сила, що діє на ланку 3 з боку ланки 0) також зобразимо у вигляді суми нормальноїі тангенціальноїскладових. Напрямок складових невідомих реакцій приймаємо довільно.

Система сил, що діє на групу (2,3), є плоскою урівноваженою.

Для визначення невідомих сил застосуємо умови рівноваги плоскої системи сил у вигляді рівнянь:

(5.2)

де - головний вектор системи сил в площині дії сил;

- алгебраїчне значення головного моменту системи сил в площині їх дії, відносно будь-якого центру О.

З першої умови в (5.2) маємо рівняння рівноваги сил, прикладених до групи (2,3):

(5.3)

В цьому рівнянні двома рисками позначені вектори, в яких напрямок і величина є відомими. Вектори, в яких відомий тільки напрямок, позначені однією рискою. Отже рівняння (5.3) має 4 невідомих параметри, що свідчить про неможливість його розв’язання шляхом графічних побудов. Цієї проблеми можна уникнути, якщо величини складових ізнайти аналітично, використовуючи рівняння моментів в умові (5.2).

Для визначення складаємо рівняння рівноваги моментів сил, що діють на ланку 2, відносно внутрішнього шарніру В:

(5.4)

Тоді Н.

Складову визначимо з рівняння рівноваги моментів сил, що діють на ланку 3, відносно того ж внутрішнього шарніру В:

(5.5)

З цього маємо Н.

Тепер складові іможуть бути знайдені графічним шляхом за допомогою побудови плану сил групи (2,3) (рис.5.2,в). Для цього, у відповідності до рівняння (5.3), побудуємо векторний многокутник сил. Приймаємо масштабний коефіцієнт побудов на плані -Н/мм.

Довжину відрізків, що зображують сили, визначимо за формулами:

(5.6)

Побудову силового многокутника проводимо в такій послідовності.

З довільної точки а відкладаємо відрізок ав, який зображує в масштабі реакцію. Далі послідовно відкладаємо сили(відрізоквс), (відрізоксd) і (відрізокde). Нормальні складові реакцій (відрізокfa) і (відрізокef ) отримаємо графічно, на перетині прямих, проведених з точок а і е у напрямку векторів і. Величини цих сил знайдемо після вимірювання відрізківfa і ef і подальшого помноження їх довжин на масштаб .

(5.7)

Повні реакції в кінематичних парах А і С знайдемо за формулами:

Н; (5.8)

Н (5.9)

Для визначення реакції запишемо рівняння рівноваги сил, прикладених до ланки 2 :

(5.10)

З плану сил (рис.5.2,в) видно, що відрізок сf відповідає реакції . Величина цієї реакції дорівнює:

Н (5.11)

Цю ж силу можна було визначити інакше, а саме, розглянувши рівновагу ланки 3. Тоді з рівняння рівноваги і плану сил для ланки 3 отримали би Н, причому.

Зауваження 1.

Слід зазначити, що нормальні складові реакцій в шарнірах А і С можна знайти не лише графічним способом. Прийнятними для цього можуть бути також графоаналітичний або аналітичний методи. Для прикладу, розглянемо визначення іза допомогою аналітичних рівнянь рівноваги моментів.

Складову визначимо з рівняння моментів сил, що діють на групу відносно точки С.

(5.12)

Складову визначимо з рівняння моментів сил, що діють на групу відносно точки А.

(5.13)

Як бачимо, результати, отримані аналітично, збігаються з попередніми результатами, що визначені за методом планів сил.

Рівновага ведучої ланки ОА.

Побудуємо кінематичну схему ведучої ланки ОА при заданому положенні механізму (рис.5.2,г). Покажемо сили, що діють на неї. В точці А з боку ланки 2 діє сила , величина и напрямок якої є відомими. (Іноді, замість силиможна зображати її складові, величина і напрямок котрих теж відомі.) Урівноважуючий момент М_УР заміняємо парою сил , прикладеною до точок О і А, перпендикулярно до ланки ОА і у напрямку М_УР. В шарнірі О зображуємо силу реакції , розклавши її на відповідні складові: нормальнуі тангенціальну. Прикладена до ланки ОА система сил є плоскою урівноваженою.

З урахуванням (5.2) складемо рівняння рівноваги сил, прикладених до ланки ОА.

(5.14)

Невідомі величини ізнайдемо с плану сил (рис.5.2,д), побудованому в масштабіН/мм. Для цього визначаємо довжину відрізків, що зображують відомі сили.

(5.15)

Побудову плану сил проводимо в такій послідовності. З довільної точки а відкладаємо відрізок ав, який зображає в масштабі силу . Далі відкладаємо силу(відрізоквс). Невідомі за величиною сили (відрізоксd) і (відрізокda) знаходимо графічно, на перетині прямих, проведених з точок а і с у напряму відповідних зусиль. Далі, складові реакції в шарнірі О знаходимо після вимірювання відрізків сd і da і помноження їх довжин на масштаб .

(5.16)

Тоді повна реакція :

Н (5.17)

Реакції в кінематичних парах знайдені.

Урівноважуючий момент М_УР можна визначити, якщо знайти хоча б одну з сил, що складають пару (рис.5.2,г). Для цього розглянемо рівняння рівноваги моментів сил, прикладених до ланки ОА, відносно точки А.

(5.18)

З цього рівняння маємо:

Н

Тоді Нм

Зауваження 2.

Урівноважуючий момент можна знайти значно простіше, якщо розглянути рівновагу моментів сил, прикладених до ланки ОА, відносно точки О.

(5.19)

Н∙м

Складову можна визначити аналітично з рівняння моментів сил, що діють на ланку відносно точки Е.

(5.20)

Звідки Н ≈ 18 Н.

Результати розрахунків збігаються з отриманими раніше.

3. Визначення урівноважуючого моменту методом М.Є.Жуковського.

Визначимо урівноважуючий момент за методом важеля Жуковського. Для цього будуємо в довільному масштабі повернутий на 90 план швидкостей (рис.5.2,е). На ньому, використовуючи теорему подібності, знаходимо положення точок а, в, с, d, S₃, , що є точками прикладання сил на плані механізму.

Переносимо всі сили паралельно до самих себе від механізму до плану швидкостей, прикладаючи їх у відповідних точках.

Складаємо рівняння моментів сил відносно полюса плану швидкостей.

. (5.21)

З плану швидкостей видно, що

Тоді

Цей результат збігається із значенням Р_УР, визначеним методом моментів.

Н·м. (5.22)

Рис.5.2

РГР – 6 Визначення геометричних параметрів нульового

зубчастого колеса нормального зовнішнього

евольвентного зачеплення

Умова завдання. На рис.6.1 зображено нормальне зовнішнє зачеплення нульових зубчастих колес із зубцями евольвентного профілю, а на рис.6.2 - одне з колес цього зачеплення. В таблиці 6 приведені відомі геометричні параметри і геометричні параметри, що треба визначити.

При розв’язанні завдання прийняти наступні позначення :

m – модуль зуба;

z – число зубців колеса;

_w – кут зачеплення;

і, якщо потрібно, застосувати наведені формули для визначення основних розмірів нульвого зубчастого колеса:

h_a = m – висота головки зуба;

h_f = 1,25m – висота ніжки зуба;

h = 2,25m – висота зуба;

– товщина зуба по ділильному колу;

p = m – крок зачеплення по ділильному колу;

– радіус ділильного кола;

–радіус початкового кола;

– радіус кола виступів зубців;

– радіус кола западин зубців;

r_в = r_w  cos_w – радіус основного кола.

Визначити: геометричні параметри, що потрібно знайти (стовбці 4-13), через задані параметри (стовбці 1-3), відповідно до варіантів (стовбець 0) за таблицею 6.

Таблиця 6

№

Задано

Визначити

0

1

2

3

4

5

6

7

8

9

10

11

12

13

1

m

rа

w

hа

hf

h

p

s

r

rw

rf

rв

z

2

z

h

w

r

rw

rf

rа

rв

hf

hа

p

s

m

3

z

hf

w

r

rw

rf

rа

hа

h

p

s

rв

m

4

p

z

w

r

rw

rа

hа

hf

h

s

rf

rв

m

5

rf

z

w

r

rw

rа

hа

hf

h

s

p

rв

m

6

rв

m

w

r

rw

rf

rа

hа

h

hf

p

s

z

7

rа

p

w

r

rw

rf

hа

hf

h

s

rв

m

z

8

rв

z

w

r

rw

rf

hа

hf

h

s

p

m

rа

9

s

rw

w

r

rf

rа

hа

hf

h

p

rв

m

z

10

p

rf

w

r

rw

rа

hа

hf

h

s

rв

m

z

11

s

rа

w

r

rw

rв

rf

hf

hа

h

p

m

z

12

m

rf

w

r

rw

rв

rа

hа

h

hf

p

s

z

13

p

rw

w

r

rf

rв

rа

hа

h

hf

s

m

z

14

hf

rf

w

r

rw

rв

rа

hа

h

s

p

m

z

15

hа

rа

w

r

rw

rв

rf

hf

h

s

p

m

z

16

m

rа

w

r

rw

rв

rf

hf

h

hа

p

s

z

17

h

z

w

hа

m

rв

s

p

hf

rа

rf

rw

r

18

hf

z

w

m

rв

s

p

hа

h

rа

rf

rw

r

19

z

p

w

m

rв

s

hf

hа

h

rа

rf

rw

r

20

z

rf

w

m

rв

s

p

hf

h

rа

hа

rw

r

21

m

rв

w

z

p

s

hа

hf

h

rа

rf

rw

r

22

r

rа

w

m

z

s

hа

hf

h

p

rf

rw

rв

23

z

rв

w

m

rа

s

p

hf

h

hа

rf

rw

r

24

rw

s

w

m

z

rв

p

hf

h

hа

rf

rа

r

25

r

p

w

m

z

s

rв

hf

h

hа

rf

rw

rа

26

rа

s

w

m

z

p

rв

hf

h

hа

rf

rw

r

27

rf

m

w

p

z

s

rв

hf

h

hа

rа

rw

r

28

rw

p

w

m

z

s

rв

hf

h

hа

rf

rа

r

29

rf

hf

w

m

z

s

p

rв

h

hа

rа

rw

r

30

rа

hа

w

m

z

s

p

rв

h

hf

rf

rw

r

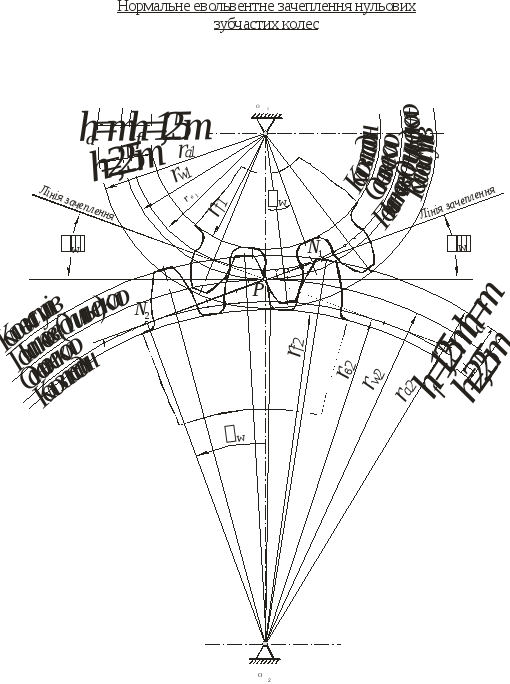
Рис. 6.1

Рис. 6.2