Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Приазовский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Прикладная механика RGR.doc

Скачиваний:

Добавлен:

05.03.2016

Размер:

16.39 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Приклад розв’язання ргр - 2

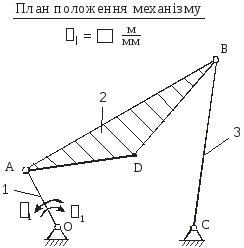
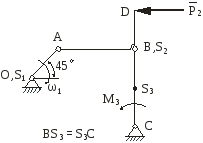
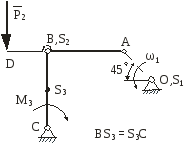
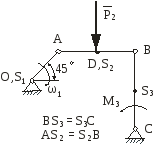
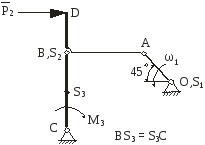
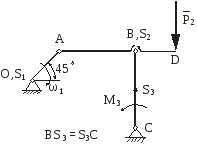
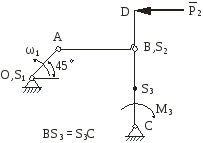
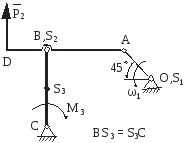
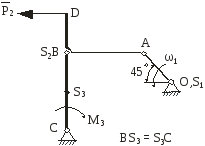
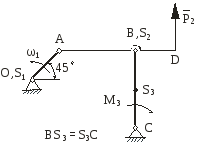
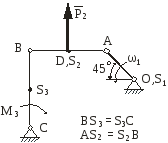
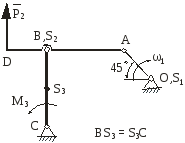
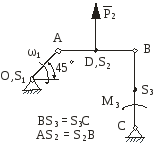
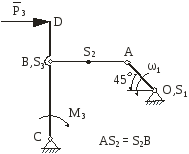
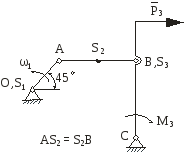
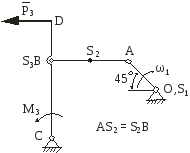
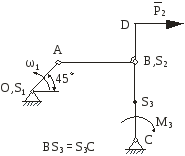
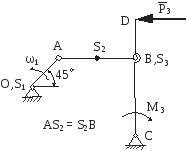
На рис.2.1 зображена кінематична схема плоского важільного механізму у заданому положенні.

Рис. 2.1

Дано:

ОА – ведуча ланка,

₁ – кутова швидкість ланки ОА;

₁ – кутове прискорення ланки ОА;

–

задані розміри.

Потрібно:

1) Побудувати запропоновану кінематичну схему механізму в заданому положенні.

2) Побудувати план швидкостей. Визначити швидкості точок А, В, D механізму і кутові швидко-сті ланок 2 і 3.

3) Побудувати план прискорень. Визначити прискорення точок А, В і D механізму і кутові приско-рення ланок 2 і 3.

Розв'язок

Побудова кінематичної схеми механізму.

Для проведення кінематичного аналізу механізму побудуємо окремо його кінематичну схему в заданому положенні, користуючись умовним масштабом _l (рис.2.2,а).^{^}

Побудова плану швидкостей. Визначення швидкостей точок А, В, D механізму і кутових швидкостей ланок 2 і 3.

Побудову плану швидкостей виконуємо у послідовності:

- побудова векторів швидкостей особливих точок (за особливі точки приймаємо точки рухомого поєднання ланок, тобто пов’язані з кінематичними парами);

- побудова векторів швидкостей інших точок, що належать механізму і потребують визначення.

а) Визначимо швидкість точки А , як точки, яка належить кривошипу ОА, що обертається навколо нерухомого центра О з кутовою швидкістю ₁:

, (м/с) (2.1)

Вектор перпендикулярний до кривошипа ОА і спрямований в бік його обертання. Швидкістьзображаємо на плані швидкостей в масштабі_v відрізком ра, приймаючи ра = 5060 мм. Тоді масштабний коефіцієнт швидкостей обчислимо за допомогою (2.2):

, (2.2)

Із довільної точки р, прийнятої за полюс плану швидкостей, відкладаємо перпендикулярно до ланки ОА вектор (рис.2.2,б). Цей вектор є вектором швидкості.

б) Визначимо швидкість точки В, яка належить кінематичній парі, що з’єднує ланки 2 і 3. Запишемо 2 векторних рівняння:

, (2.3)

де

Розв’язуємо систему рівнянь (2.3) графічно. Для цього через точку а проведемо пряму, перпендикулярну до АВ, а через точку с, яка збігається з полюсом р, проведемо пряму, перпендикулярну до ВС. На перетині цих перпендикулярів відмічаємо точку в. Вектор зображає абсолютну швидкість точки В. Напрям швидкості визначається напрямком вектора . Векторзображає швидкістьточки В у відносному обертанні навколо точки А.

в) Швидкість точки D знайдемо з векторних рівнянь:

. (2.4)

Розв’язуємо цю систему рівнянь графічно. Через точку а проведемо пряму, перпендикулярну до DА, а через точку в – пряму, перпендикулярну до DB. На перетині цих перпендикулярів відмічаємо точку d. Вектор відображає абсолютну швидкість.

План швидкостей побудовано.^{^}

г) Використовуючи план швидкостей, знаходимо величини швидкостей точок і кутових швидкостей ланок.

Лінійні швидкості точок, (м/с):

(2.5)

Кутові швидкості ланок 2 і 3 , (рад/с):

(2.6)

Визначимо напрями кутових швидкостей ₂і ₃. Для цього умовно переносимо вектор в точку В і розглянемо рух точки В відносно точки А. Знаходимо, що₂спрямована за годинниковою стрілкою. Аналогічно, переносимо векторв точку В і розглянемо рух точки В відносно точки С. Бачимо, що₃також спрямована за годинниковою стрілкою. Наносимо ці напрями кутових швидкостей на план механізму (рис.2.2,а).

Побудова плану прискорень. Визначення прискорень точок А, В, D механізму і кутових прискорень ланок 2 і 3.

Побудову плану прискорень виконуємо у послідовності:

- побудова векторів прискорень особливих точок (точки рухомого поєд-нання ланок);

- побудова векторів прискорень інших точок, що належать механізму і потребують визначення.

а) Визначимо прискорення точки А , як точки, яка належить кривошипу ОА, що обертається з миттєвою кутовою швидкістю ₁ і кутовим прискоренням ₁.

Повне прискорення точки А дорівнює геометричній сумі нормального та тангенціального прискорень:

(2.7)

Модулі цих прискорень знайдемо за формулами:

(м/с²) (2.8)

(м/с²) (2.9)

Зображаємо прискорення відрізкомn₁. Приймаємо n₁=7080мм. Тоді масштабний коефіцієнт прискорень:

, (2.10)

З довільної точки , прийнятої за полюс плану прискорень, відкладаємо вектор , спрямований паралельно ланці ОА від точки А до точки О. Через точкуn₁ проводимо вектор , який в масштабізображає прискорення. Довжину відрізкаn₁а знаходимо за формулою:

, (мм) (2.11)

Цей вектор, перпендикулярний до ОА, і спрямований за напрямком кутового прискорення ₁. З’єднавши прямою точки  і а, отримаємо вектор . Цей вектор є вектором повного прискорення точки А.

б) Визначимо прискорення точки В, як точки, яка належить водночас ланкам 2 і 3, що виконують плоско-паралельний рух.^{^}

Запишемо два векторних рівняння:

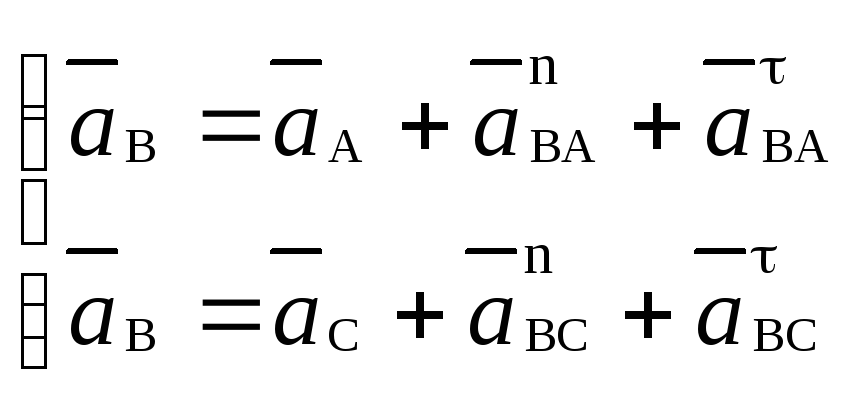(2.12)

Прискорення а_С=0, тому що точка С нерухома.

Величини нормальних прискорень обчислюються за формулами:

(м/с²); (м/с²) (2.13)

В прийнятому масштабі ці прискорення зобразимо відрізками аn₂ і n₃.

Величини цих відрізків дорівнюють:

, (мм); , (мм) (2.14)

Розв’язуємо систему (2.12) графічно. З точки а відкладаємо відрізок аn₂, який зображає вектор . Відрізокаn₂проводимо паралельно до ланки АВ в напрямі від точки В до точки А. Через точку n₂ проводимо перпендикулярно до АВ пряму, по якій буде спрямований вектор . Відповідно другому рівнянню системи (2.12) з полюса паралельно ВС в напрямі від В до С відкладаємо відрізок n₃. Через точку n₃ перпендикулярно до ВС проводимо пряму, по якій буде спрямований вектор до перетину в точців з прямою, по якій спрямований вектор . Відрізокв зображає вектор прискорення точки В. Відрізкиn₂в і n₃в – тангенціальні прискорення ,. З’єднавши прямою точкиа і в, отримаємо відрізок ав, що зображає вектор .

в) Прискорення точки D знаходиться побудовою , подібногоі з подібним розташуванням вершин, тому що теорема подібності, сформульована для плану швидкостей, справедлива і для плану прискорень.

З плану прискорень визначаємо величини прискорень, (м/с²):

(2.15)

г) Величини кутових прискорень ₂ і ₃ знаходимо з формул:

, (рад/с²) ; , (рад/с²) (2.16)

Визначаємо напрями кутових прискорень ₂ і ₃. Умовно перенесемо вектор в точку В і розглянемо рух точки В навколо точки А. Виходячи з цього, знаходимо, що прискорення₂спрямовано проти ходу годинникової стрілки. Перенесемо вектор в точку В і розглянемо її рух навколо точки С. Бачимо, що₃ спрямовано також проти ходу годинникової стрілки. Наносимо ці кутові прискорення на план механізму (рис.2.2,а).

Графічна частина

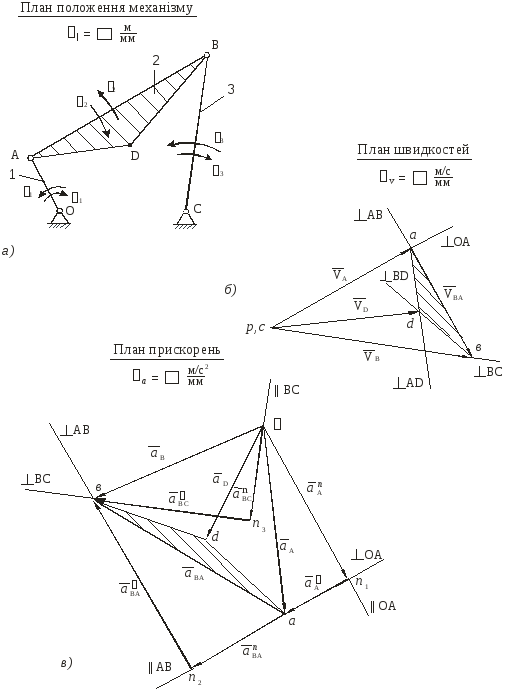
Рис.2.2

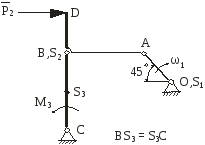
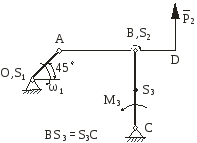
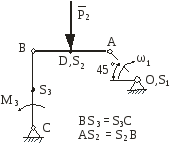
РГР - 3 Зведення сил (моментів сил) і мас (моментів інерції) в плоских важільних механізмах

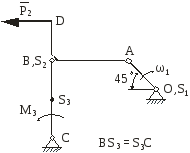
Умова завдання. Дана кінематична схема механізму в певному положенні (таблиця 3). На механізм діють сила Р_i і момент сил М₃, прикладені відповідно до i-ої і 3-ої ланки. Маси ланок і моменти інерції відносно центрів мас відомі. Відомі також геометричні розміри ланок і положення їх центрів мас. Задані чисельні параметри: сила Р_i=1000 Н; момент сили М₃=100 Н·м; інерційні характеристики - m₂=2 кг; m₃=10 кг; ;;; геометричні розміри -