4.2. Виды записи уравнений относительного движения ротора синхронного генератора

Уравнение относительного движения имеет вид

,

(4.41)

где - электрическая мощность генератора;

- демпферный коэффициент (мощность демпфирования);

- момент турбины (механический момент).

Упрощенно (при ) можно получить, что

,

(4.42)

где - механическая мощность турбины.

Если не учитывается явление демпфирования (), то

.

(4.43)

В уравнениях (4.41)-(4.43) все величины выражены в относительных единицах. Иногда используются другие варианты записи уравнений (4.41)-(4.43), в которых все или некоторые переменные выражены в именованных единицах. Так, например, если угол выражен в электрических градусах, время и постоянная инерции– в секундах и мощности – в относительных единицах, то уравнение (4.43) приобретает вид

,

(4.44)

где - частота тока в сети.

Другие варианты записи уравнения движения ротора приведены в учебнике [1].

5. Простейшие методы оценки устойчивости

5.1. Практические критерии статической устойчивости

Если малые возмущения приводят к прогрессирующему изменению параметров режима, то система будет неустойчивой. В начале эти изменения происходят очень медленно, проявляясь в виде самопроизвольного изменения, называемого сползанием (текучестью) параметров режима системы. Условия возникновения такого нарушения устойчивости можно выявить на основе анализа соотношений, характеризующих режим системы.

В качестве примера рассмотрим систему, включающую две станции, работающие через сопротивления ина общую нагрузку (рис. 5.1).

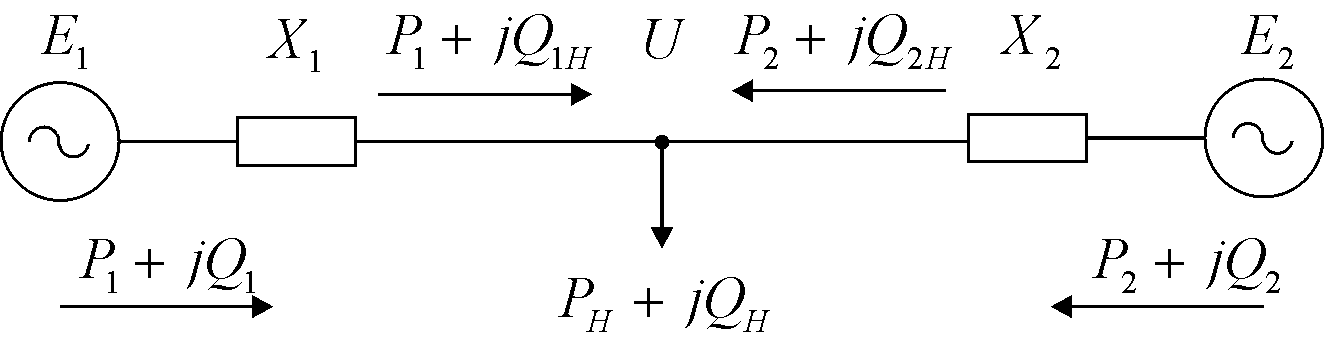
Рис. 5.1. Исследуемая система

Установившийся режим этой системы характеризуется определенными зависимостями:

,

(5.1)

где ,,,- активные и реактивные мощности, отдаваемые генераторами первой и второй станций;

и- активная и реактивная мощности в узле нагрузки;

,мощности турбин первой и второй станций;

- напряжение в узле, к которому подключена нагрузка;

и- углы между векторами ЭДС станций,и напряжения;

- угловая частота тока в сети.

Зависимости (5.1) представляют собой статические характеристики (т.к. не зависят от скорости изменения параметров).

В установившемся режиме уравнения моментов на валах генераторов

,

(5.2)

где и- электромагнитные моменты генераторов первой и второй станций;

и- механические моменты (моменты турбин) этих станций.

При малых медленных изменениях режима в относительных единицах , поэтому вместо выражений (5.2) будем использовать равенства

.

(5.3)

Кроме того, можно записать уравнения баланса активной и реактивной мощности в рассматриваемой сети

(5.4)

Отклонения режима могут быть вызваны различными факторами, например, изменением мощности одной из турбин, активной и реактивной мощности нагрузки. Предположим, что происходит одновременное воздействие всех этих факторов. Тогда для станций и нагрузки можно записать уравнения баланса активной и реактивной мощности при отклонении режима от исходного

(5.5)

При малых отклонениях параметров производные, входящие в систему уравнений (5.5), можно считать постоянными величинами. Предположим, что известны значения изменений мощности ,,и, тогда с помощью уравнений (5.5) можно найти любое из отклонений параметров режима. Например,

,

(5.6)

где - главный определитель системы уравнений (5.5);

,,,- миноры этого определителя.

При этом

.

(5.7)

Отклонения параметров ,имогут быть найдены с помощью выражений аналогичных выражению (5.6).

Если при неравных нулю минорах определитель окажется равным нулю, то любое очень малое отклонение величин,,иможет вызвать неограниченно большое изменение параметров режима,,и, т.е. параметры режима будут самопроизвольно уползать от исходных значений. Таким образом, критерием критического режима, разделяющего устойчивые и неустойчивые режимы, будет условие

.

(5.8)

Использование критериев, основанных на условии (5.8), позволяет выявить тенденции системы к неустойчивости без учета характера движения, зависящего от инерционных постоянных системы. Эти критерии выявляют только возможную текучесть режима (сползание, апериодическую неустойчивость), не позволяя выявить неустойчивость, которая может проявиться в виде колебаний (колебательную неустойчивость, самораскачивание).

Принимая постоянными те или иные параметры режима, из условия (5.8) можно получить частные критерии – практические критерии устойчивости.

Так считая, что не меняются частота тока, напряжение в узловой точке и мощности турбин станций, с учетом выражений (5.5) получаем

	(5.9)
и	(5.10)
или ,	(5.11)
.	(5.12)

На основании выражений (5.11) и (5.12) можно сделать вывод о том, что критический по устойчивости режим наступит при

,

(5.13)

где

или для схемы, изображенной на рис. 5.1,

и.

(5.14)

В случае генератора, отдающего мощность системе несоизмеримо большей мощности (рис. 2.14в), критерий предельного режима

.

(5.15)

При этом предполагается, что ЭДС генератора и напряжение на шинах подстанции системынеизменны.

Если пренебречь активными сопротивлениями, то

,

(5.16)

где суммарное реактивное сопротивление, включающее сопротивление генератора и сети, которая связывает генератор и подстанцию системы.

Предел передаваемой мощности

.

(5.17)

Критический режим, соответствующий выполнению условия (5.15), наступит в точке 1 (рис. 5.2).

Рис. 5.2. Характеристики мощности, отдаваемой генератором в сеть, и мощности турбины

Из устойчивого режима можно получить неустойчивый его утяжелением, например увеличением нагрузки. Сопоставляя параметры существующего устойчивого режима с параметрами нового режима, полученного в результате утяжеления и лежащего на границе между устойчивым и неустойчивым режимами, т. е. критического режима, можно рассчитатькоэффициент запаса статической устойчивостипо параметру:

.

(5.18)

Например, для генератора, отдающего мощность системе (рис. 2.14в),

(5.19)

Рассмотрим узел нагрузки (рис. 5.1). Принимаем, что частота тока неизменна () и сохраняется баланс активной мощности в узле нагрузки (). Из последнего уравнения системы (5.5) можно получить

или	(5.20)
.	(5.21)

Обозначив реактивную мощность, поступающую в узел от генераторов как

,

(5.22)

критерий предельного режима можно записать в виде

или	(5.23)
,	(5.24)

где .

В этом случае коэффициент запаса статической устойчивости может быть определен как

,

(5.25)

где - критическое напряжение, при котором выполняется условие (5.24).

Рассмотрим систему, включающую несколько станций, подключенных к общей узловой точке с нагрузкой (рис. 5.3).

Рис. 5.3. Многомашинная система с узловой точкой, к которой подключена нагрузка

Нагрузки задана статическими характеристиками . При сохранении баланса активной мощности и неизменных ЭДС станций критерий предельного режима для узлаkможет быть записан как

,

(5.26)

где

;	(5.27)
,	(5.28)

а коэффициент запаса статической устойчивости найден с помощью выражения (5.25).

Если рассмотреть асинхронный двигатель, питающийся от шин с неизменным напряжением, то критерием предельного режима будет

,

(5.29)

где - активная мощность, потребляемая двигателем;

- скольжение двигателя.

Другие практические критерии узлов нагрузки будут рассмотрены в дальнейшем.

Каждый из практических критериев статической устойчивости имеет ограниченную область применения, которая зависит от принятых при выводе критерия допущений и схемы.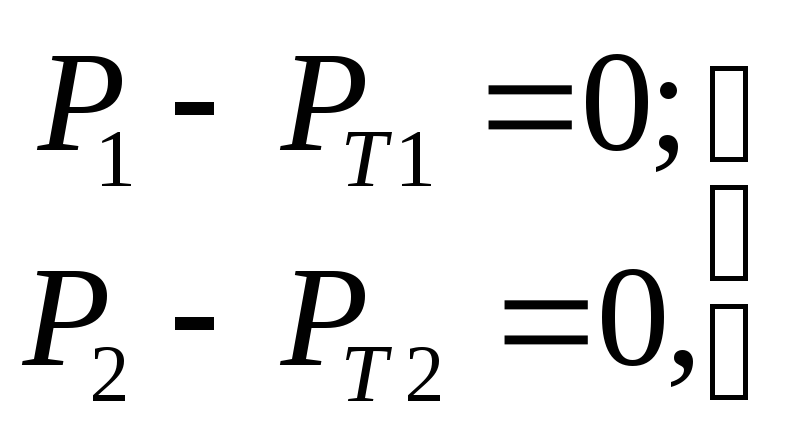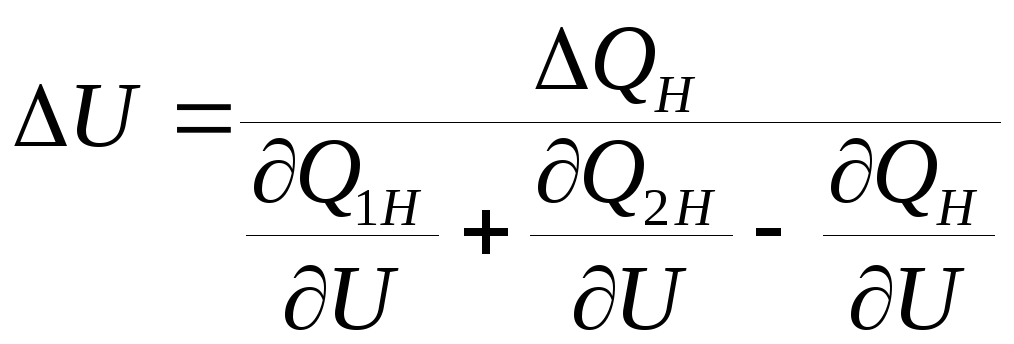