4. Основные уравнения электромеханических переходных процессов

4.1. Система относительных единиц

Вспомните, для чего использовалась в курсе «Электромагнитные переходные процессы» система относительных единиц, каким образом выбирались базисные единицы, как осуществлялся переход из именованных единиц в относительные. Вспомните, что представляют собой «приближенное и точное приведение параметров схем замещения». Что понимают под коэффициентом трансформации трансформаторов при приведении параметров схем замещения?

Величины в системе относительных единиц выражаются в долях некоторых величин, принятых за единицы измерения и называемых базисными. Так при расчетах электромагнитных переходных процессов используют базисные величины: ток , напряжение, мощностьи сопротивление. Две из этих величин выбираются произвольно, а остальные две рассчитываются с использованием выражений

и	(4.1)
.	(4.2)

Иногда принимают

,

(4.3)

считая, что значение введено в ток, т.е. величина тока завышена враза. В этом случае для перехода от значения тока в относительных единицахк значению в именованных единицахследует использовать соотношение

.

(4.4)

В частности, в учебнике [1] используются соотношения (4.3) и (4.4).

При рассмотрении электромеханических переходных процессов система относительных единиц должна быть дополнена и другими базисными величинами.

В качестве базисного времени принимают время, в течение которого ротор, вращающийся с синхронной угловой скоростью, повернется на 1 рад.

Тогда и

.

(4.5)

Время в относительных единицах

.

(4.6)

При частоте тока в сети Гц

.

(4.7)

О времени, выраженном в относительных единицах, говорят, что оно имеет размерность радиан.

Угол поворота ротора обычно выражают в электрических радианах или электрических градусах. Электрический угол , выраженный в радианах или градусах, связан с геометрическим углом, выраженным в аналогичных единицах, с помощью соотношения

,

(4.8)

где - число пар полюсов рассматриваемой электрической машины.

При исследовании электромеханических переходных процессов различают абсолютную механическую скорость , абсолютную электрическую скорость, относительную механическую скоростьи относительную электрическую скоростьротора.

Абсолютная механическая скоростьротора представляет собой производную геометрического смещенияротора по времени

.

(4.9)

Соответственно абсолютная электрическая скорость

.

(4.10)

При этом углы иотсчитываются от неподвижной оси. Абсолютные механическая и электрическая скорости связаны между собой соотношением

.

(4.11)

Относительной скоростьюназывается скорость по отношению к вращающейся оси. Обычно относительная скорость определяется по отношению к оси, вращающейся с синхронной скоростью. Тогда,относительная электрическая скорость

и	(4.12)
,	4.13)

где - относительный угол, т.е. электрический угол по отношению к вращающейся оси.

Относительная электрическая скорость, выраженная в относительных единицах

,

(4.14)

где - базисная угловая скорость.

Обычно в качестве базисной выбирают синхронную угловую скорость , тогда

.

(4.15)

Если величина угла выражена в электрических радианах, а времени – в секундах иГц, то

рад/с.

(4.16)

В этом случае выражение (4.15) приобретает вид

.

(4.17)

При выражении угла в электрических градусах, а времени в секундах,

.

(4.18)

Относительная механическая скорость

	(4.19)
или ,	(4.20)

где - синхронная механическая скорость.

Относительные механическая и электрическая скорости, выраженные в относительных единицах (в долях от синхронной скорости), численно равны:

.

(4.21)

Электромагнитная мощность может быть выражена через вращающий моменти скорость

,

(4.22)

или в относительных единицах

.

(4.23)

Поскольку

,

(4.24)

то

.

(4.25)

Если угол выражен в электрических радианах или электрических градусах, то

	(4.26)
или .	(4.27)

Если , то можно принять, что.

Ускорение ротора, с^-2, может быть найдено как

,

(4.28)

где - избыток вращающего момента,;

- момент инерции,.

Из выражения (4.28)

,

(4.29)

где - кинетическая энергия, запасенная ротором при его движении с синхронной скоростью;

- постоянная инерции,.

Постоянная инерции численно равна удвоенному значению кинетической энергии ротора, вращающегося с синхронной скоростью.

Из выражения (4.29) можно получить

(4.30)

или, выражая угол поворота ротора в электрических радианах:

.

(4.31)

Если имеет размерность рад/с,- МВт,-, товыражено в рад/с².

Из выражения (4.31), разделив числитель и знаменатель на , можно получить

,

(4.32)

где имеет размерность рад/с²,- с,- безразмерная величина.

Выражая угол поворота в электрических радианах, получаем

, град/с2,

(4.33)

где имеет размерность МВт,-,

или

,

(4.34)

где постоянная выражена в секундах.

В этом случае постоянная инерции численно равна времени разгона ротора генератора от неподвижного состояния до синхронной скорости при условии, что на ротор действует постоянный вращающий момент, равный номинальному, и что момент сопротивления постоянен.

Постоянная инерции может быть найдена как

,

(4.35)

где - маховый момент,;

- частота вращения ротора, об/мин;

выражена в секундах и- в МВА.

Если время выразить в относительных единицах, то можно получить

,

(4.36)

где

	(4.37)
и .	(4.38)

иявляются безразмерными величинами.

Приращение энергии ротора при изменении его скорости

,

(4.39)

откуда

.

(4.40)
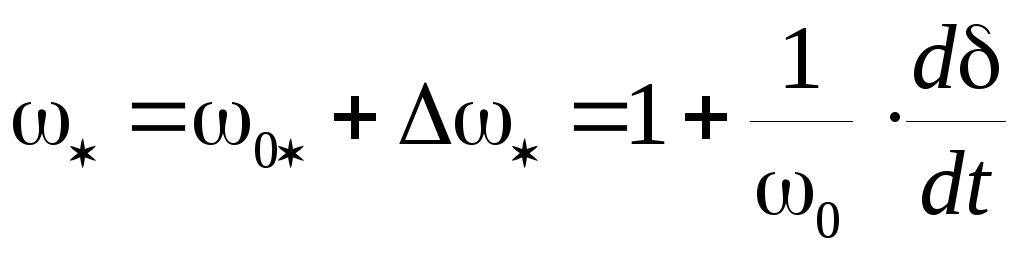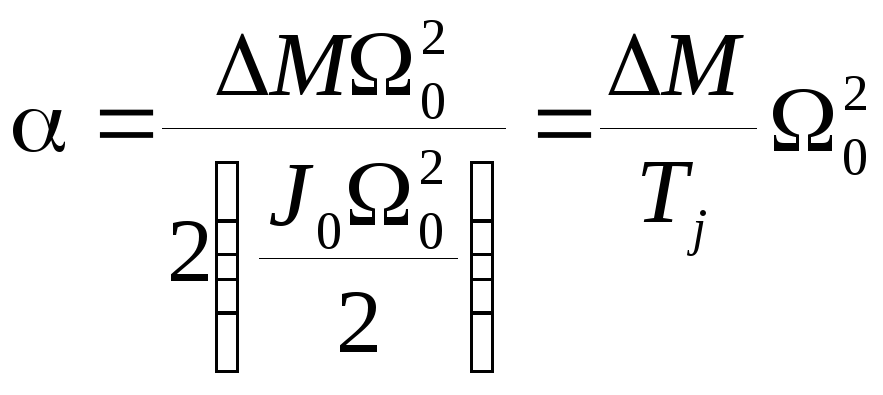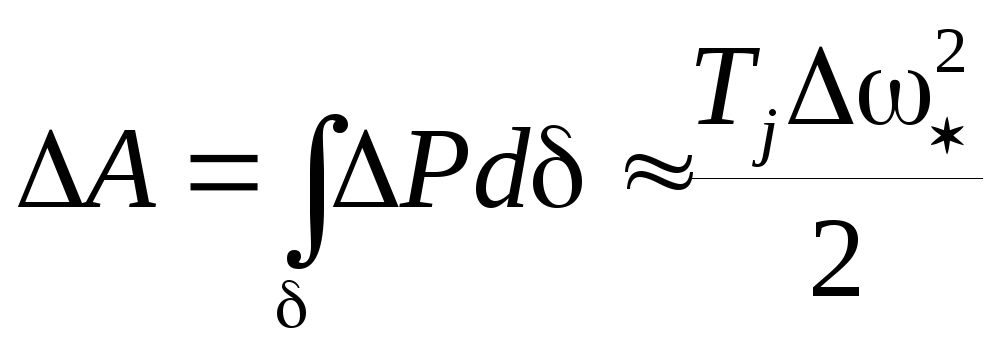